Pflichtteil 2
Aufgabe P1
a)
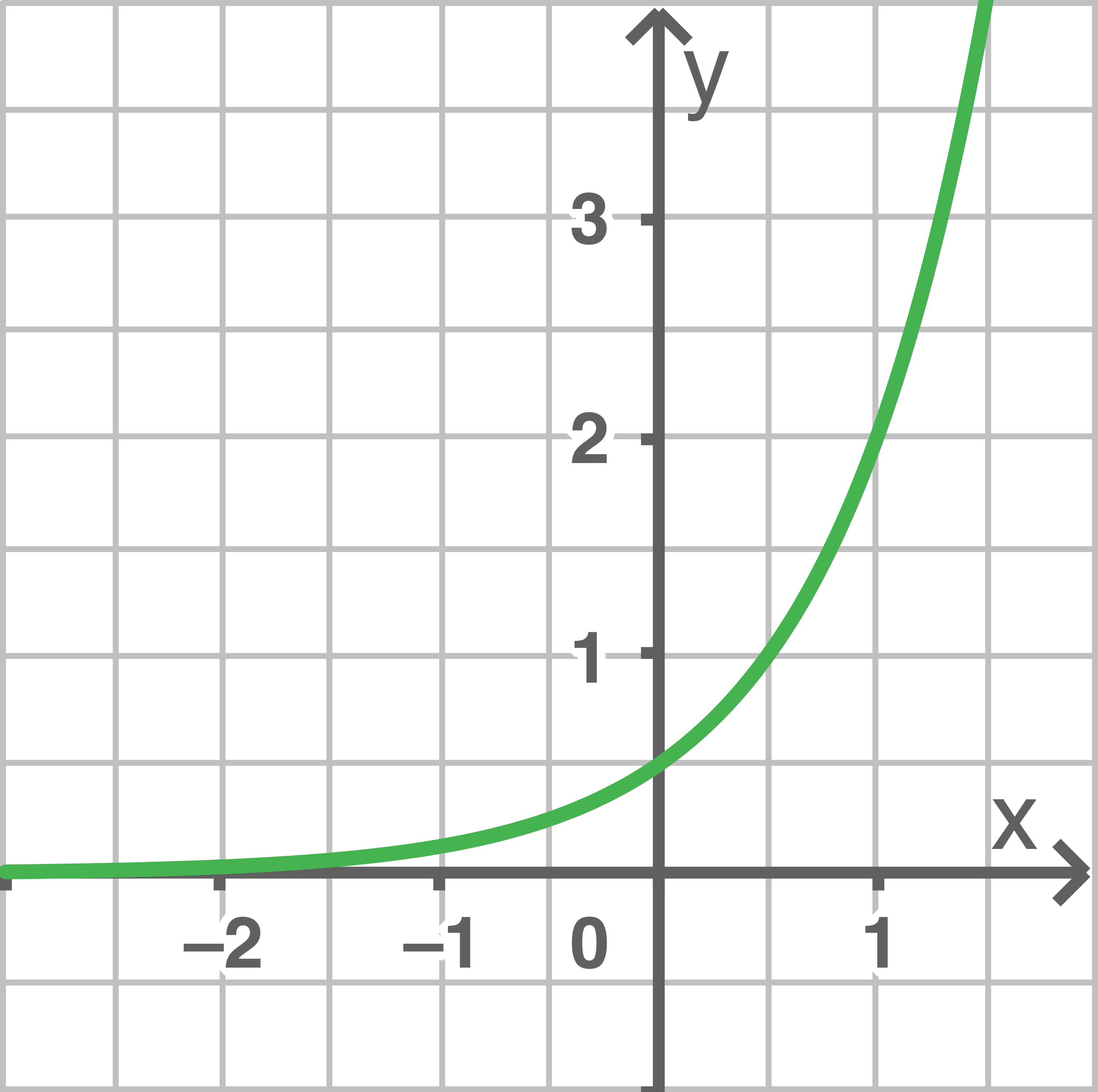
Die Abbildung zeigt den Graphen der Funktion 
mit 
mit 
und 
. Bestimme die passenden Werte von 
und 
.
(3 BE)
b)
Der Graph der in 
definierten Funktion 
mit 
wird um 2 in negative 
-Richtung verschoben.
Zeige, dass der dadurch entstehende Graph auch durch eine Streckung des Graphen von in 
-Richtung erzeugt werden kann.
Zeige, dass der dadurch entstehende Graph auch durch eine Streckung des Graphen von
(2 BE)
Aufgabe P2
a)
Eine ganzrationale Funktion hat die Nullstellen 1,2 und -3.
Gib eine Funktionsgleichung für an.
Gib eine Funktionsgleichung für
(2 BE)
b)
Für eine Funktion 
gilt: 
Bestimme die Extremstellen des Graphen von
Bestimme die Extremstellen des Graphen von
(3 BE)
Aufgabe P3
Gegeben ist die inBestimme diejenige reelle Zahl
(5 BE)
Aufgabe P4
In einer Gemeinde gab es beim Streit um ein neues Bauprojekt eine Befragung. Von den Teilnehmenden waren
a)
Bestimme das Ergebnis der Befragung.
(3 BE)
b)
Bestimme unter den Teilnehmenden, die für das Projekt stimmten, den Anteil der höchstens 35-Jährigen.
(2 BE)
Aufgabe P5
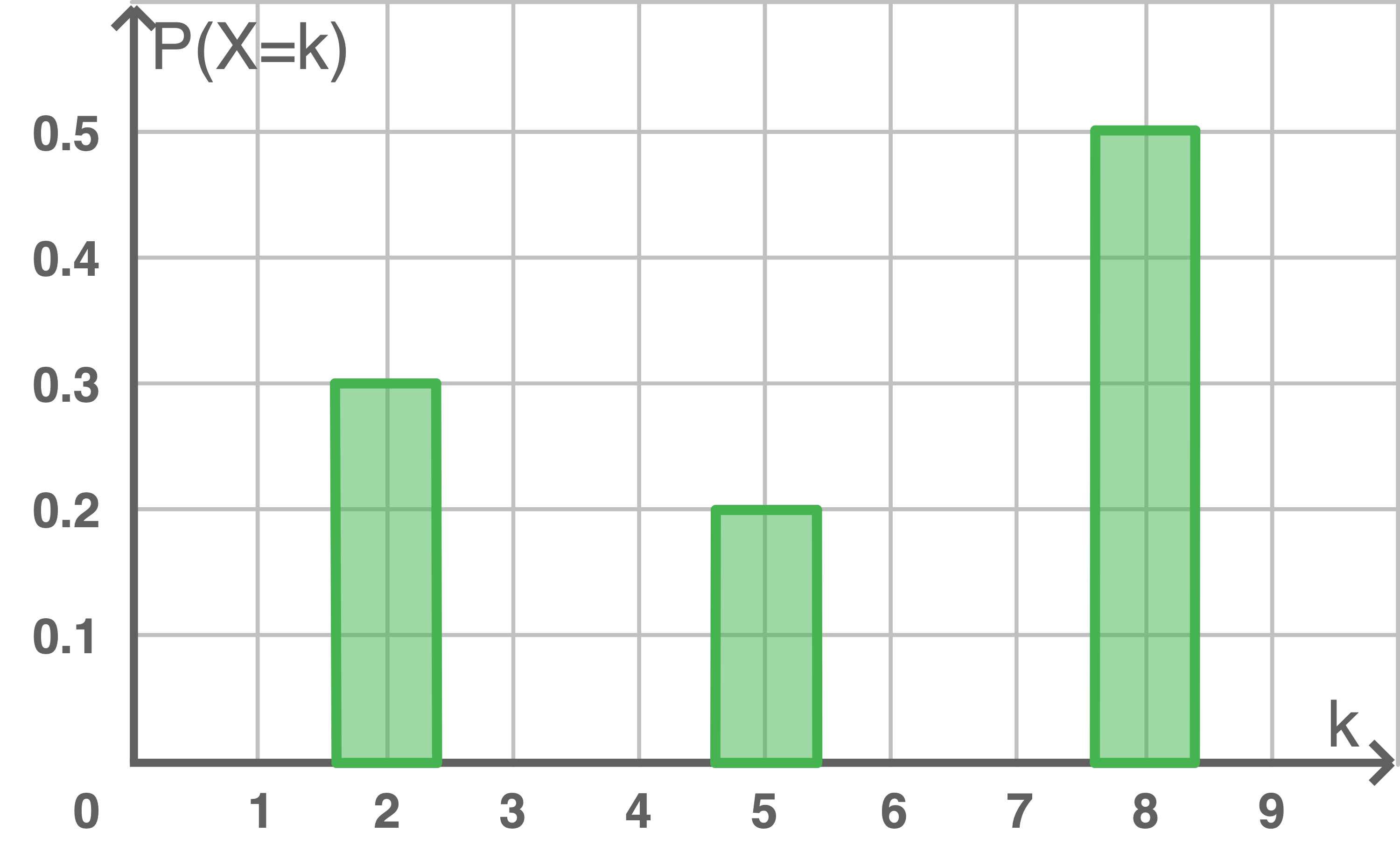
Für ein Zufallsexperiment wird eine Zufallsgröße 
festgelegt, welche die drei Werte 2, 5 und 8 annehmen kann. In der Abbildung ist die Wahrscheinlichkeitsverteilung von dargestellt.
| 2 | 5 | 8 | |
| 0,2 |
a)
Gib die in der Tabelle fehlenden Werte an.
Berechne den Erwartungswert von
Berechne den Erwartungswert von
(3 BE)
b)
Das Zufallsexperiment wird zweimal unter gleichen Bedingungen durchgeführt. Dabei wird jeweils der Wert der Zufallsgröße notiert.
Bestimme die Wahrscheinlichkeit dafür, dass das Produkt dieser beiden Werte den Wert 10 ergibt.
Bestimme die Wahrscheinlichkeit dafür, dass das Produkt dieser beiden Werte den Wert 10 ergibt.
(2 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung P1
a)
Am Graphen kann 
und 
abgelesen werden. Daraus folgt:
![\(\begin{array}[t]{rll}
f(0)&=& \dfrac{1}{2} \\[5pt]
a \cdot b^0 &=& \dfrac{1}{2} \\[5pt]
a &=& \dfrac{1}{2} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/dc2782220d9aaceafc7cb8cb587bc177f686e9e0f266f63569059d53213efa1a?color=5a5a5a)
Desweiteren gilt:
![\(\begin{array}[t]{rll}
f(1) &=& 2 \\[5pt]
\dfrac{1}{2} \cdot b^1 &=& 2 &\quad \scriptsize \mid\; \cdot 2 \\[5pt]
b &=& 4
\end{array}\)](https://mathjax.schullv.de/cc38ee0db83d1b39786a506a14e47ca123753b1a404fb7c8fea45670ccb7b8e1?color=5a5a5a)
b)
Lösung P2
a)
Eine ganzrationale Funktion mit den Nullstellen 
und 
ist beispielsweise:
b)
1.Schritt: Notwendige Bedingung für Extremstellen anwenden
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/78d991a788ff24e6a8c0a1b62cf00e289c55b5b87be47737d9ceb3e72cadca64?color=5a5a5a)
Mit der 
-Formel folgt:
![\(\begin{array}[t]{rll}
x_{1/2}&=&-\dfrac{-2}{2} \pm \sqrt{\left(\dfrac{-2}{2}\right)^2-(-24)} \\[5pt]
x_{1/2}&=&1 \pm \sqrt{25} \\[5pt]
x_{1/2}&=& 1 \pm 5
\end{array}\)](https://mathjax.schullv.de/417b7fde8da5d3885e9c7037198aa4b8f95f521ac0b0454d2dce46901e7eeec4?color=5a5a5a)
2. Schritt: Hinreichende Bedingung für Extremstellen anwenden
Es gilt: 
Die Extremstellen des Graphen von folgen mit 
und 
Lösung P3
Schnittstellen der beiden Graphen:
![\(\begin{array}[t]{rll}
f(x) &=& y \\[5pt]
x^2 &=& m \cdot x &\quad \scriptsize \mid\; -m \cdot x \\[5pt]
x^2 - m \cdot x &=& 0 \\[5pt]
x \cdot (x - m) &=& 0 \\[5pt]
x_1 &=& 0 \\[5pt]
x_2 &=& m
\end{array}\)](https://mathjax.schullv.de/11c7f5853385a6efed93e09d141cef6ed23a8a63894e3b657c9ca0a428d92f7f?color=5a5a5a)
Flächeninhalt zwischen den beiden Graphen:
![\(\begin{array}[t]{rll}
\displaystyle\int_{m}^{0}y-f(x)\;\mathrm dx &=& 36 \\[5pt]
\displaystyle\int_{m}^{0} \left(m \cdot x-x^{2}\right) \;\mathrm dx&=& 36 \\[5pt]
\left[\dfrac{1}{2} m \cdot x^{2}-\dfrac{1}{3} x^{3}\right]_{m}^{0} &=& 36 \\[5pt]
-\dfrac{1}{2} m^{3}+\dfrac{1}{3} m^{3}&=& 36 \\[5pt]
-\dfrac{1}{6} m^{3} &=& 36 &\quad \scriptsize \mid\; \cdot (-6) \\[5pt]
m^{3} &=& -6^3 &\quad \scriptsize \mid\; \sqrt[3]{\;} \\[5pt]
m &=& -6
\\[5pt]
\end{array}\)](https://mathjax.schullv.de/8153f7228faa1235502a134ed63bffc32841997c125ce121b9ffa05b5edda2f8?color=5a5a5a)
Lösung P4
a)
Nach Aufgabenstellung sind 
der Befragen über 35 Jahre. 
von ihnen sind gegen das Bauprojekt. 
der Befragen sind höchstens 
Jahre alt. 
von ihnen sind gegen das Bauprojekt. Somit sind 
der Befragten gegen das Bauprojekt und 
dafür.
b)
Lösung P5
a)
| 2 | 5 | 8 | |
| 0,1 | 0,2 | 0,5 |
b)
Das Produkt 10 kann hier auf zwei Wegen (
oder 
) erreicht werden . Damit ergibt sich die Wahrscheinlichkeit: 