Aufgabe 3B
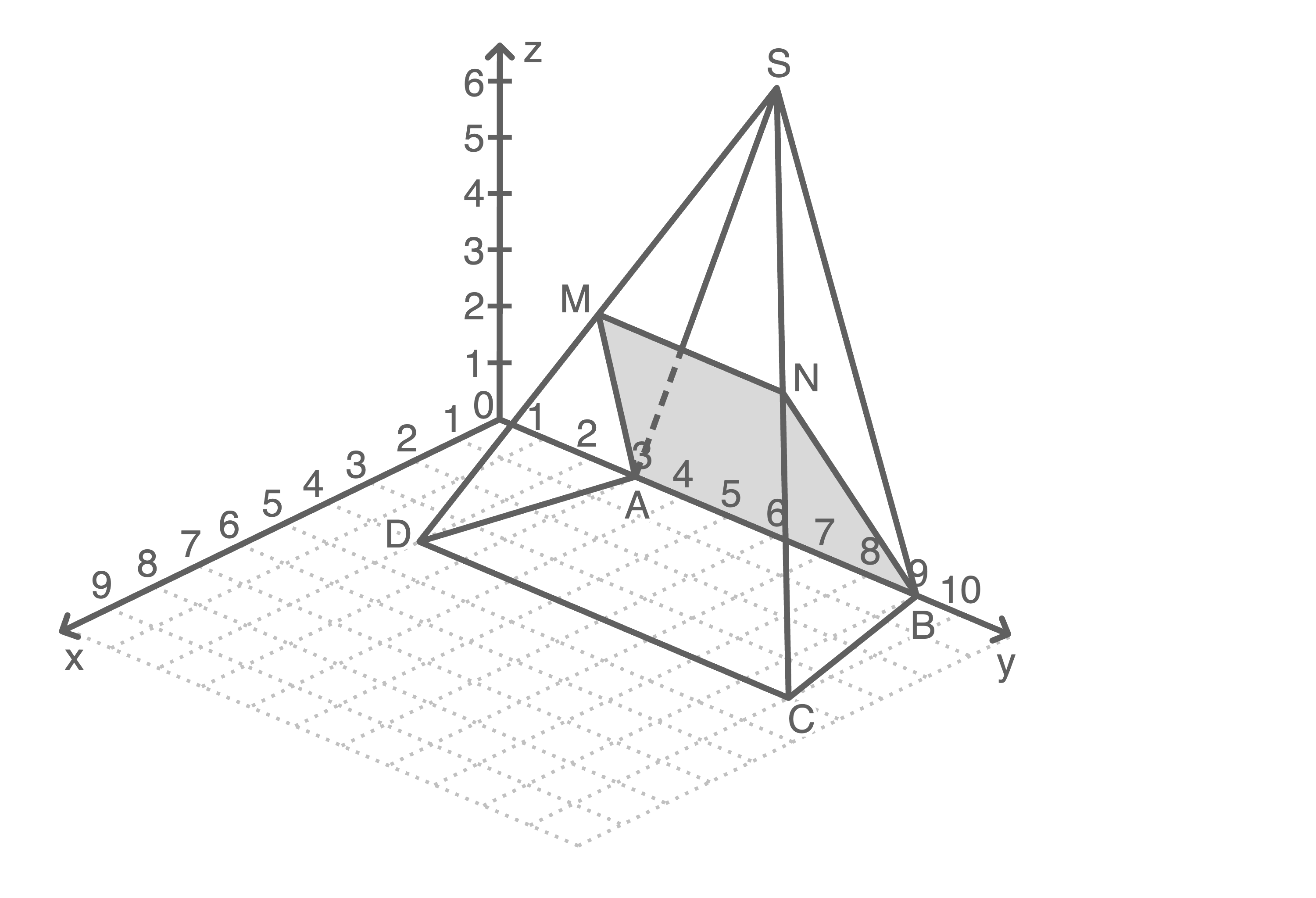
Die Abbildung zeigt die Pyramide 
mit 
und 
sowie der Spitze im Punkt 
.
bezeichnet den Mittelpunkt der Kante 
und 
bezeichnet den Mittelpunkt der Kante 
a)
Begründe, dass das Dreieck 
gleichschenklig ist.
Bestimme eine Gleichung für die Gerade, auf der die Symmetrieachse des Dreiecks liegt.
(6 BE)
b)
Berechne den von den Kanten 
und 
eingeschlossenen Winkel.
Die Punkte
(4 BE)
c)
Begründe, dass die Punkte 
und 
die folgenden Koordinaten haben:
mit 
mit 
(5 BE)
d)
Untersuche, ob es einen Punkt sowie einen Punkt gibt, sodass das Viereck 
ein Rechteck ist.
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Gleichschenkligkeit begründen
Ein Dreieck ist genau dann gleichschenklig, wenn zwei Seiten genau gleich lang sind.
Es gilt:
Mit 
folgt also, dass das Dreieck 
gleichschenklig ist.
Gleichung bestimmen
Die Symmetrieachse des Dreiecks verläuft durch den Mittelpunkt der Strecke 
sowie durch die Spitze 
Es gilt:
![\(\begin{array}[t]{rll}
\overrightarrow{OP}&=& \dfrac{1}{2}\cdot \left(\overrightarrow{OC}+\overrightarrow{OD}\right)& \\[5pt]
&=& \dfrac{1}{2}\cdot \left(\pmatrix{4\\10\\0}+\pmatrix{4\\2\\0}\right)& \\[5pt]
&=& \pmatrix{4\\6\\0}
\end{array}\)](https://mathjax.schullv.de/eb935b43f84200a6d0339aa33a7b7a8de29cf7618c25d2c5aff01adc4a16934b?color=5a5a5a)
Eine Gleichung für die Gerade, auf der die Symmetrieachse liegt, folgt also mit:
![\(\begin{array}[t]{rll}
g: \overrightarrow{x}&=& \overrightarrow{OS}+ \lambda \cdot \overrightarrow{PS}& \\[5pt]
&=& \pmatrix{0\\6\\8} + \lambda \cdot \pmatrix{4\\0\\-8}
\end{array}\)](https://mathjax.schullv.de/37735f4dd66fb04baecf44e981606c50bc9a5a4c7658865517e765f097bcad2f?color=5a5a5a)
b)
Es gilt:
![\(\begin{array}[t]{rll}
\overrightarrow{OM}&=& \dfrac{1}{2}\cdot \left(\overrightarrow{OD}+\overrightarrow{OS}\right) & \\[5pt]
&=& \dfrac{1}{2}\cdot \left(\pmatrix{4\\2\\0}+\pmatrix{0\\6\\8}\right)& \\[5pt]
&=& \pmatrix{2\\4\\4}
\end{array}\)](https://mathjax.schullv.de/ed9eec67f81fafea9ca205d3aee5275acea0f3054d4923a09909a6cc823a7288?color=5a5a5a)
Für den Winkel folgt also:
![\(\begin{array}[t]{rll}
\cos \alpha&=& \dfrac{\mid \overrightarrow{A M} \circ \overrightarrow{A B}\mid}{\mid\overrightarrow{A M}| \cdot|\overrightarrow{A B}\mid} & \\[5pt]
\cos \alpha&=& \dfrac{\left| \pmatrix{2\\1\\4} \circ \pmatrix{0\\6\\0} \right|}{\left| \pmatrix{2\\1\\4} \right|\cdot \left| \pmatrix{0\\6\\0} \right|} & \\[5pt]
\cos \alpha&=& \dfrac{2\cdot 0+1\cdot 6+4\cdot 0}{\sqrt{2^2+1^2+4^2}\cdot 6}& \\[5pt]
\cos \alpha&\approx& 0,218& \quad \scriptsize \mid\; \cos ^{-1} \\[5pt]
\alpha&\approx & 77^\circ
\end{array}\)](https://mathjax.schullv.de/d763e8ead06f9810152e05bd4e3be7dc4a5da70284afbf572363f148b36e3d98?color=5a5a5a)
Die Kanten 
und 
schließen somit einen Winkel von etwa 
ein.
c)
d)
Die Strecken 
und 
müssen senkrecht zur 
-Achse sein.
Die -Koordinate von muss also 3 sein. Es soll also gelten:
![\(\begin{array}[t]{rll}
2+4q&=& 3 &\quad \scriptsize \mid\; -2 \\[5pt]
4q&=& 1 &\quad \scriptsize \mid\; :4 \\[5pt]
q&=& \dfrac{1}{4}
\end{array}\)](https://mathjax.schullv.de/8a59f2710db1ca4fe7d5a29456008307b180c0eb7fa62a7028e2b4a514709e9d?color=5a5a5a)
Analog muss die -Koordinate von den Wert 9 haben. Es folgt also:
![\(\begin{array}[t]{rll}
10-4p&=& 9 &\quad \scriptsize \mid\; -10\\[5pt]
-4p&=& -1 &\quad \scriptsize \mid\; :(-4)\\[5pt]
p&=& \dfrac{1}{4}
\end{array}\)](https://mathjax.schullv.de/8150edb5b014c5e2bbcbff94ffe14fd6a7b460f84cb95b8bbde714c05ba91a24?color=5a5a5a)
Für die Punkte und mit 
ist das Viereck 
somit ein Rechteck.