Aufgabe 1B
Beim maschinellen Lernen simuliert man das Verhalten von menschlichen Nervenzellen. Dabei entscheidet eine künstliche Zelle mithilfe einer sogenannten Aktivierungsfunktion, ob sie ein Signal ausgibt. Die Funktion  mit
mit  ,
,  , ist eine mögliche Aktivierungsfunktion.
, ist eine mögliche Aktivierungsfunktion.  wird als Eingangswert und
wird als Eingangswert und  als Aktivitätsmaß bezeichnet.
als Aktivitätsmaß bezeichnet.
a)
Berechne für den Eingangswert  das Aktivitätsmaß.
das Aktivitätsmaß.
Markiere in Abbildung 1 den Bereich auf der -Achse, für den das Aktivitätsmaß mindestens
-Achse, für den das Aktivitätsmaß mindestens  und höchstens
und höchstens  beträgt.
beträgt.
Berechne die Eingangswerte, für die
Markiere in Abbildung 1 den Bereich auf der
- das Aktivitätsmaß
überschritten wird,
- die lokale Änderungsrate des Aktivitätsmaßes mit der durchschnittlichen Änderungsrate auf dem Intervall
;
übereinstimmt.
(12 BE)
b)
Eine Aktivierungsfunktion soll die folgenden Kriterien erfüllen:
 im Intervall
im Intervall  ;
; ![\(2]\)](https://mathjax.schullv.de/bc7f92128ec1c4bc007613e34d772f39de483a5c38658907082d03f682d12005?color=5a5a5a) diese Kriterien erfüllt, und begründe deine Entscheidung.
diese Kriterien erfüllt, und begründe deine Entscheidung.
- Die Steigung des Funktionsgraphen in der Intervallmitte ist maximal.
- Der Inhalt der Fläche zwischen dem Funktionsgraphen und der
-Achse im Intervall
;
ist kleiner als
des Inhalts der Fläche zwischen dem Funktionsgraphen und der
-Achse im gesamten Intervall.
(8 BE)
c)
Unabhängig vom Sachkontext werden nun die auf ganz  definierten Funktionen
definierten Funktionen  mit
mit
 betrachtet.
Es gilt
betrachtet.
Es gilt  Die Gleichung
Die Gleichung  hat in Abhängigkeit von
hat in Abhängigkeit von  die Lösungen
die Lösungen 
 und
und  .
Bestimme den Wert von
.
Bestimme den Wert von  , für den der Graph von
, für den der Graph von  genau zwei Nullstellen hat.
genau zwei Nullstellen hat.
Berechne den Wert von , für den
, für den  eine Nullstelle ist.
eine Nullstelle ist.
Bestimme den Wert von , für den eine der drei Nullstellen genau in der Mitte zwischen den beiden anderen liegt.
, für den eine der drei Nullstellen genau in der Mitte zwischen den beiden anderen liegt.
Jeder Graph von , hat einen Wendepunkt
, hat einen Wendepunkt  .
.
Untersuche, ob es einen Wert von gibt, sodass die Tangente an den Graphen von
gibt, sodass die Tangente an den Graphen von  im Wendepunkt die
im Wendepunkt die  -Achse unter einem Winkel von
-Achse unter einem Winkel von  schneidet.
schneidet.
Berechne den Wert von
Bestimme den Wert von
Jeder Graph von
Untersuche, ob es einen Wert von
(14 BE)
a)
Aktivitätsmaß für  bestimmen:
bestimmen:

Das Aktivitätsmaß für beträgt
beträgt  .
.
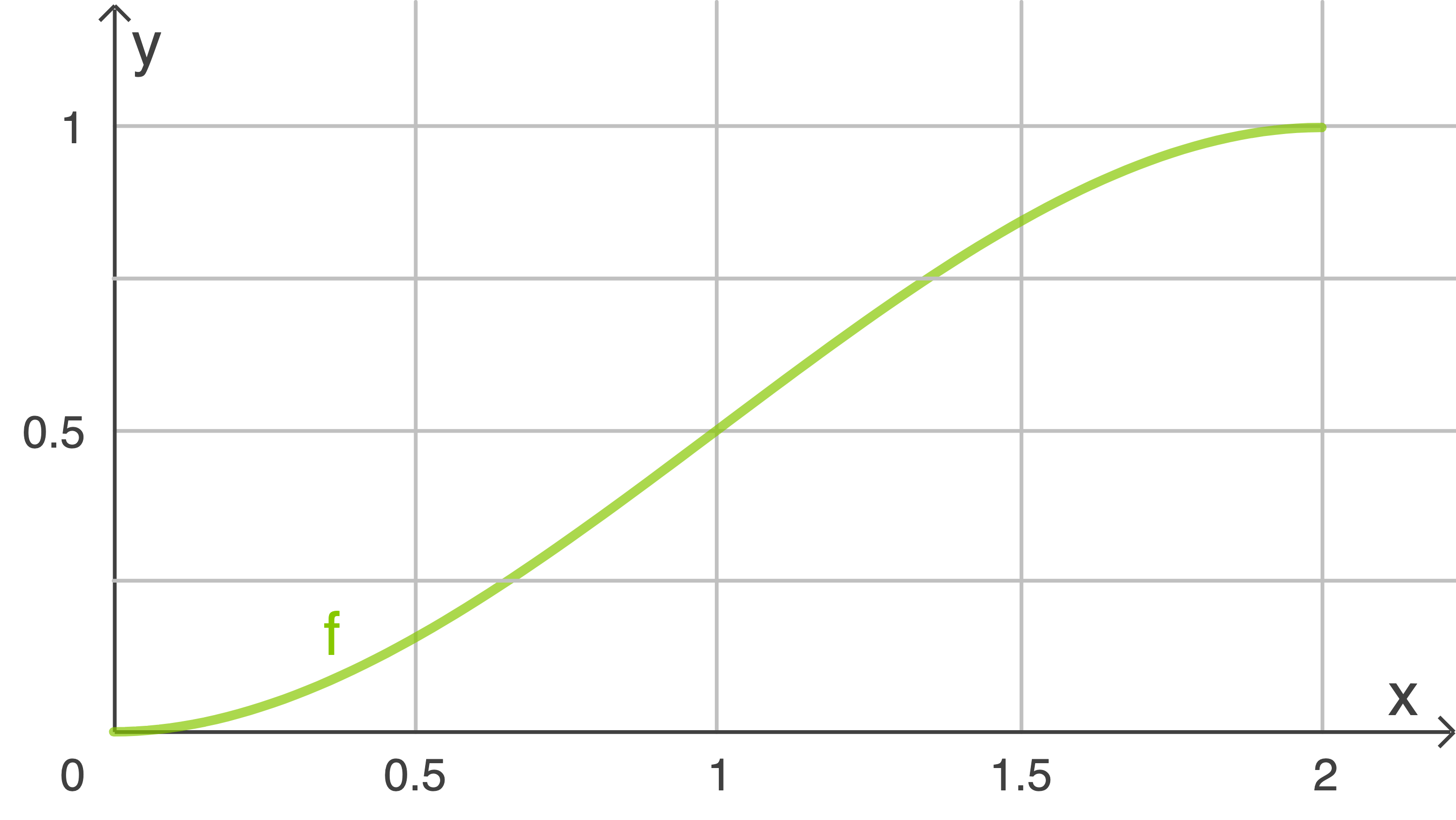
Bereich:
Definiere und
und  .
.
Die Markierung des Intervalls befindet sich von etwa bis etwa
bis etwa  auf der x-Achse.
auf der x-Achse.
 lösen:
lösen:
Definiere eine Gerade mit
mit  .
.
 TI 84-PLUS
Bestimme den Schnittpunkt des Graphen von
TI 84-PLUS
Bestimme den Schnittpunkt des Graphen von  mit der Gerade zu
mit der Gerade zu 
 Casio fx-CG
Bestimme den
Casio fx-CG
Bestimme den  -Wert zum
-Wert zum  -Wert
-Wert  mit dem X-CAL-Befehl.
Der Schnittpunkt des Graphen von
mit dem X-CAL-Befehl.
Der Schnittpunkt des Graphen von  mit der Gerade zu
mit der Gerade zu  befindet sich bei
befindet sich bei  .
.
 liefert im Intervall
liefert im Intervall ![\([0;2]\)](https://mathjax.schullv.de/843d839ab55e0f672f243636b5611ab923c075cc63ed4cbee0bdb8f535440b7a?color=5a5a5a) die Lösungen
die Lösungen  .
Für
.
Für  wird das Aktivitätsmaß
wird das Aktivitätsmaß  überschritten.
überschritten.
Eingangswerte berechnen:
Die durchschnittliche Änderungsrate auf dem Intervall![\([0 ; 2]\)](https://mathjax.schullv.de/b397e6702378a78dc30b1aa169a908bbe1f3c1e578fd08018963998620212206?color=5a5a5a) entspricht der Steigung der Sekante durch die Punkte
entspricht der Steigung der Sekante durch die Punkte  und
und  .
.
![\(\begin{array}[t]{rll}
m&=&\dfrac{f(2)-f(0)}{2-0} &\quad \\[5pt]
&=&\dfrac{1-0}{2}&\quad \\[5pt]
&=&\dfrac{1}{2}& \quad
\end{array}\)](https://mathjax.schullv.de/ec0405829cb367c596deae729789d7be9a1da2c518044093fbf3f3d295033e78?color=5a5a5a) Die durchschnittliche Änderungsrate auf dem Intervall
Die durchschnittliche Änderungsrate auf dem Intervall ![\([0 ; 2]\)](https://mathjax.schullv.de/b397e6702378a78dc30b1aa169a908bbe1f3c1e578fd08018963998620212206?color=5a5a5a) beträgt
beträgt  .
.
Die lokale Änderungsrate (Ableitung) entspricht der Steigung der Tangente in einem entsprechenden Punkt.
Gesucht sind die -Werte, für die
-Werte, für die  gilt.
gilt.
 Definiere eine Gerade
Definiere eine Gerade  mit
mit  .
.
 TI 84-PLUS
Bestimme die Schnittpunkte des Graphen von
TI 84-PLUS
Bestimme die Schnittpunkte des Graphen von  mit der Geraden zu
mit der Geraden zu 
 Casio fx-CG
Bestimme den
Casio fx-CG
Bestimme den  -Wert zum
-Wert zum  -Wert
-Wert  mit dem X-CAL-Befehl.
Die Schnittpunkte des Graphen von
mit dem X-CAL-Befehl.
Die Schnittpunkte des Graphen von  mit der Geraden zu
mit der Geraden zu  befinden sich bei
befinden sich bei  und
und  .
Für die Eingangswerte
.
Für die Eingangswerte  und
und  stimmt die lokale Änderungsrate des Aktivitätsmaßes mit der durchschnittlichen Änderungsrate auf dem Intervall
stimmt die lokale Änderungsrate des Aktivitätsmaßes mit der durchschnittlichen Änderungsrate auf dem Intervall ![\([0 ; 2]\)](https://mathjax.schullv.de/b397e6702378a78dc30b1aa169a908bbe1f3c1e578fd08018963998620212206?color=5a5a5a) überein.
überein.
Das Aktivitätsmaß für
Bereich:
Definiere
Die Markierung des Intervalls befindet sich von etwa
Definiere eine Gerade
2nd  trace (calc)
trace (calc)  5: intersect
5: intersect
F5 (G-Solv)  F6
F6  F2: X-CAL
F2: X-CAL
Eingangswerte berechnen:
Die durchschnittliche Änderungsrate auf dem Intervall
Die lokale Änderungsrate (Ableitung) entspricht der Steigung der Tangente in einem entsprechenden Punkt.
Gesucht sind die
2nd  trace (calc)
trace (calc)  5: intersect
5: intersect
F5 (G-Solv)  F6
F6  F2: X-CAL
F2: X-CAL
b)
Kriterien für eine Aktivierungsfunktion überprüfen:
Steigung des Funktionsgraphen in der Intervallmitte ist maximal.
Dieses Kriterium ist erfüllt, falls der Funktionsgraph von an der Stelle
an der Stelle  einen Hochpunkt hat.
einen Hochpunkt hat.
Der Hochpunkt wird mit Hilfe des GTRs bestimmt.
 TI 84-PLUS
TI 84-PLUS
 Casio fx-CG
Der Hochpunkt befindet sich bei
Casio fx-CG
Der Hochpunkt befindet sich bei  .
.
Daraus folgt, dass die Steigung des Funktionengraphen in der Intervallmitte maximal ist und dieses Kriterium erfüllt die Funktion .
.
Der Inhalt der Fläche zwischen dem Funktionsgraphen und der x-Achse im Intervall ![\([0 ; 1]\)](https://mathjax.schullv.de/60ef2388f7a38bd1534c70712bfde18b0eab3dfd578c8ff9c5f3634456c7a2fa?color=5a5a5a) ist kleiner als
ist kleiner als  des Inhalts der Fläche zwischen dem Funktionsgraphen und der x-Achse im gesamten Intervall.
des Inhalts der Fläche zwischen dem Funktionsgraphen und der x-Achse im gesamten Intervall.
Berechne mit Hilfe des GTRs die folgenden Integrale:
 und
und 
 TI 84-PLUS
TI 84-PLUS
 Casio fx-CG
Casio fx-CG
![\(\begin{array}[t]{rll}
\displaystyle\int_{0}^{1}f(x)\;\mathrm dx&\approx&0,19 &\quad \\[5pt]
\dfrac{1}{5} \cdot \displaystyle\int_{0}^{2}f(x)\;\mathrm dx&=&\dfrac{1}{5} \cdot 1&\quad \\[5pt]
&=&0,2 \gt 0,19
\end{array}\)](https://mathjax.schullv.de/add49b17fe59b739c51b8b2e6777294d6b46fd138e88230175dc8f0cbe6082ca?color=5a5a5a) Der Inhalt der Fläche zwischen dem Funktionsgraphen und der x-Achse im Intervall
Der Inhalt der Fläche zwischen dem Funktionsgraphen und der x-Achse im Intervall ![\([0 ; 1]\)](https://mathjax.schullv.de/60ef2388f7a38bd1534c70712bfde18b0eab3dfd578c8ff9c5f3634456c7a2fa?color=5a5a5a) ist kleiner als
ist kleiner als  des Inhalts der Fläche zwischen dem Funktionsgraphen und der x-Achse im gesamten Intervall.
des Inhalts der Fläche zwischen dem Funktionsgraphen und der x-Achse im gesamten Intervall.
Daraus folgt, dass die Funktion dieses Kriterium erfüllt.
Die Funktion
dieses Kriterium erfüllt.
Die Funktion  erfüllt im Intervall
erfüllt im Intervall ![\([0 ; 2]\)](https://mathjax.schullv.de/b397e6702378a78dc30b1aa169a908bbe1f3c1e578fd08018963998620212206?color=5a5a5a) die Kriterien einer Aktivierungsfunktion.
die Kriterien einer Aktivierungsfunktion.
Dieses Kriterium ist erfüllt, falls der Funktionsgraph von
Der Hochpunkt wird mit Hilfe des GTRs bestimmt.
2nd  trace (calc)
trace (calc)  4: maximum
4: maximum
F5 (G-Solv)  F2: MAX
F2: MAX
Daraus folgt, dass die Steigung des Funktionengraphen in der Intervallmitte maximal ist und dieses Kriterium erfüllt die Funktion
Berechne mit Hilfe des GTRs die folgenden Integrale:
2nd  trace (calc)
trace (calc)  7:
7: 
F5 (G-Solv)  F6
F6  F3:
F3: 
Daraus folgt, dass die Funktion
c)
Wert von  bestimmen, für den der Graph von
bestimmen, für den der Graph von  genau zwei Nullstellen hat:
genau zwei Nullstellen hat:
erste Nullstelle:
Für den Graph von existieren genau zwei Nullstellen, wenn
existieren genau zwei Nullstellen, wenn  gilt, das heißt
gilt, das heißt  .
.
Für den Wert hat der Graph von
hat der Graph von  genau zwei Nullstellen (
genau zwei Nullstellen ( und
und  ).
).
Wert von bestimmen, für den
bestimmen, für den  eine Nullstelle ist:
eine Nullstelle ist:
Hierfür ist zu lösen.
Alternativ kann obige Gleichung auch mit dem GTR gelöst werden (Schnittpunkt zweier Geraden).
Für den Wert
zu lösen.
Alternativ kann obige Gleichung auch mit dem GTR gelöst werden (Schnittpunkt zweier Geraden).
Für den Wert  besitzt der Graph von
besitzt der Graph von  bei
bei  eine Nullstelle.
eine Nullstelle.
Wert von bestimmen, für den eine der drei Nullstellen genau in der Mitte zwischen den beiden anderen liegt:
bestimmen, für den eine der drei Nullstellen genau in der Mitte zwischen den beiden anderen liegt:
Zu beobachten ist, dass
 die untere Nullstelle,
die untere Nullstelle,
 die mittlere Nullstelle und
die mittlere Nullstelle und
 die obere Nullstelle ist.
Daraus folgt, dass
die obere Nullstelle ist.
Daraus folgt, dass  ist, sodass die Nullstelle
ist, sodass die Nullstelle  genau in der Mitte zwischen den anderen beiden Nullstellen liegt.
Hierfür ist
genau in der Mitte zwischen den anderen beiden Nullstellen liegt.
Hierfür ist  zu lösen.
Alternativ kann obige Gleichung auch mit dem GTR gelöst werden (Schnittpunkt zweier Geraden).
Für den Wert
zu lösen.
Alternativ kann obige Gleichung auch mit dem GTR gelöst werden (Schnittpunkt zweier Geraden).
Für den Wert  liegt eine der drei Nullstellen genau in der Mitte zwischen den anderen beiden Nullstellen.
liegt eine der drei Nullstellen genau in der Mitte zwischen den anderen beiden Nullstellen.
Der Graph der Funktion besitzt dann seine Nullstellen bei
besitzt dann seine Nullstellen bei  ,
,  und
und  .
.
Wert von bestimmen, sodass die Tangente an den Graphen von
bestimmen, sodass die Tangente an den Graphen von  im Wendepunkt die x-Achse unter einem Winkel von
im Wendepunkt die x-Achse unter einem Winkel von  schneidet:
schneidet:
![\(\begin{array}[t]{rll}
f_a](https://mathjax.schullv.de/b41629caa4c7a19f28421719c51db00eafd14a133f8544dc9907e061d56d2afd?color=5a5a5a) Gesucht wird ein Wert für
Gesucht wird ein Wert für  , sodass die Steigung der Tangente an den Graphen von
, sodass die Steigung der Tangente an den Graphen von  im Wendepunkt
im Wendepunkt  beträgt.
beträgt.
Gesucht wird ein Wert für , sodass die Steigung der Tangente an den Graphen von
, sodass die Steigung der Tangente an den Graphen von  im Wendepunkt
im Wendepunkt  beträgt.
beträgt.
Für schneidet die Tangente an den Graphen von
schneidet die Tangente an den Graphen von  im Wendepunkt die x-Achse unter einem Winkel von
im Wendepunkt die x-Achse unter einem Winkel von  .
.
erste Nullstelle:
Für den Graph von
Für den Wert
Wert von
Hierfür ist
Wert von
Zu beobachten ist, dass
Der Graph der Funktion
Wert von
Gesucht wird ein Wert für
Für
 Aufgabe 1B a) Graph.png)