Aufgabe 3C

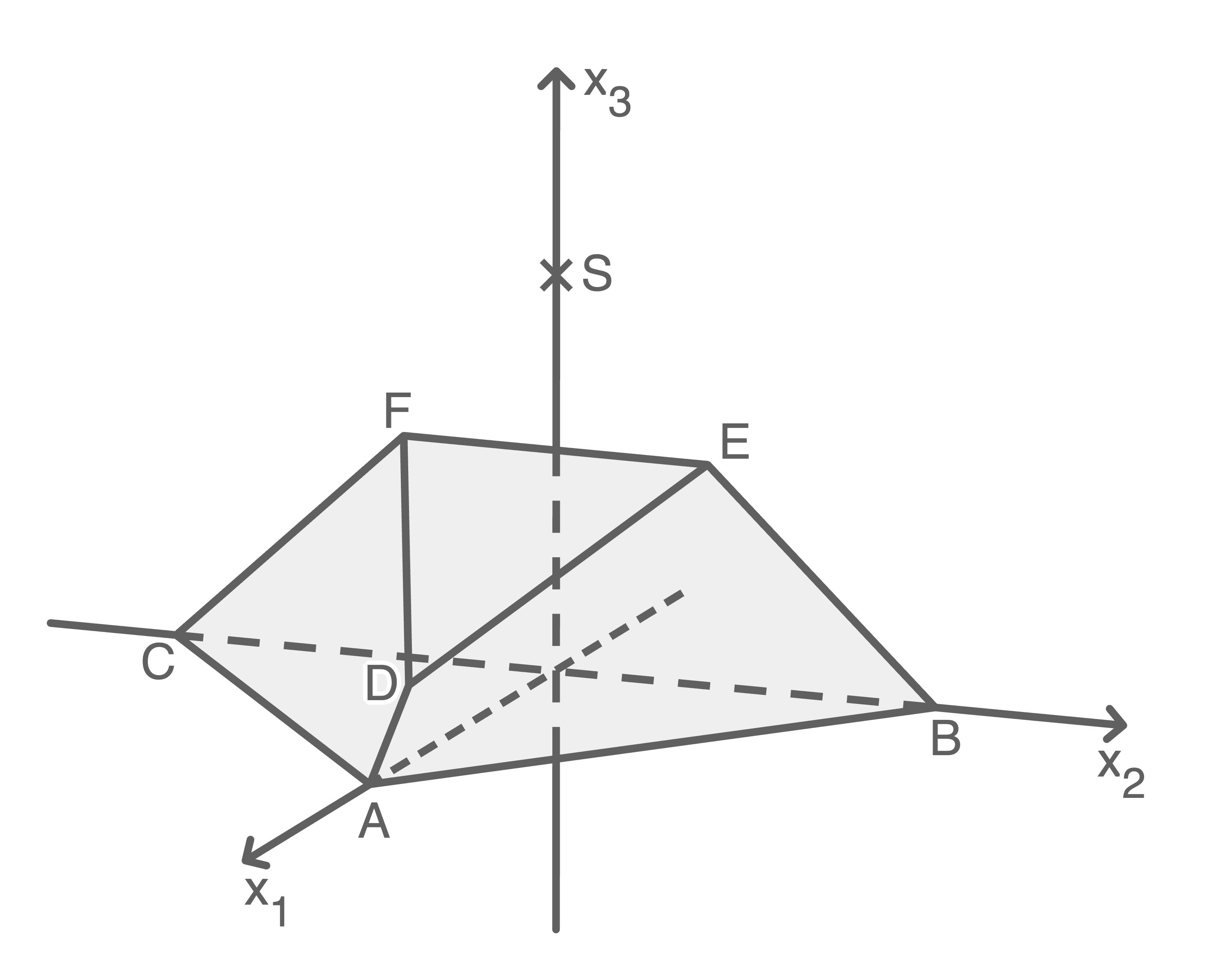
Die Abbildung zeigt den Körper $A B C D E F$ mit $A(10\mid 0\mid 0)$ , $B(0\mid7,5\mid 0),$ $C(0\mid-7,5\mid 0),$ $D(8\mid0\mid 1),$ $E(0\mid3\mid 3)$ und $F(0\mid-3\mid 3).$

Das Dreieck $A B C$ wird als Grundfläche und das Dreieck $D E F$ als Deckfläche des Körpers bezeichnet. Die Deckfläche liegt in der Ebene $L.$

Koerper Deckflaeche Dreieck Niedersachsen Mathe Abi

Zeige, dass das Dreieck $A B C$ gleichschenklig ist.

Berechne den Innenwinkel des Dreiecks $A B C$ im Eckpunkt $A.$

Begründe, dass die Kante $\overline{E F}$ parallel zur Grundfläche liegt.

(7 BE)

Der Körper $A B C D E F$ kann zu einer Pyramide mit der Grundfläche $A B C$ und der Spitze $S$ ergänzt werden, wobei $D, E$ und $F$ auf den Kanten der Pyramide liegen.

Begründe, dass $S$ in der $x_2 x_3$ -Ebene liegt.

Berechne die Koordinaten von $S.$

$\big[$ Zur Kontrolle: $S(0\mid 0\mid 5) \big]$

(5 BE)

$S$ ist auch Spitze einer Pyramide mit der Grundfläche $D E F.$ Die untenstehende Abbildung zeigt in der $x_1 x_3$ -Ebene die Punkte $D$ und $S$ sowie den Mittelpunkt $M$ der Kante $\overline{E F}.$

Begründe, dass der Abstand von $S$ zur Ebene $L$ kleiner als 2 ist, und veranschauliche deine Begründung durch geeignete Eintragungen in der untenstehenden Abbildung.

Eintragungen Skizze Pyramide Niedersachsen Mathe Abi

(4 BE)

Für $t \in[0 ; 1]$ besitzen die Punkte $D_t$ der Strecke $\overline{D S}$ die $x_1$ -Koordinate $8-8 t.$

$A_{E F S}$ ist der Flächeninhalt des Dreiecks $EFS.$

Begründe, dass das Volumen der Pyramide $E F S D_t$ mit dem Term $\dfrac{1}{3} \cdot A_{E F S} \cdot(8-8 t)$ berechnet werden kann.

Beschreibe ein Vorgehen zur Berechnung des Volumens des Körpers $A B C D_t E F.$

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Gleichschenkligkeit zeigen

Ein Dreieck ist genau dann gleichschenklig, wenn zwei Seiten genau gleich lang sind.

Es gilt:

$\left|\overrightarrow{AB}\right|=\left| \pmatrix{-10\\7,5\\0} \right| = 12,5$

$\left|\overrightarrow{AC}\right|=\left| \pmatrix{-10\\-7,5\\0} \right| = 12,5$

Mit $|\overrightarrow{AB}|=|\overrightarrow{AC}|$ folgt also, dass das Dreieck $ABC$ gleichschenklig ist.

Innenwinkel berechnen

Rechnung anzeigen

$\alpha \approx 74^\circ$

Parallelität begründen

Die Grundfläche liegt in der $x_1 x_2$ -Ebene.

Da die Punkte $E$ und $F$ die gleiche $x_3$ -Koordinate haben, liegt die Strecke $\overline{EF}$ parallel zur $x_1x_2$ -Ebene.

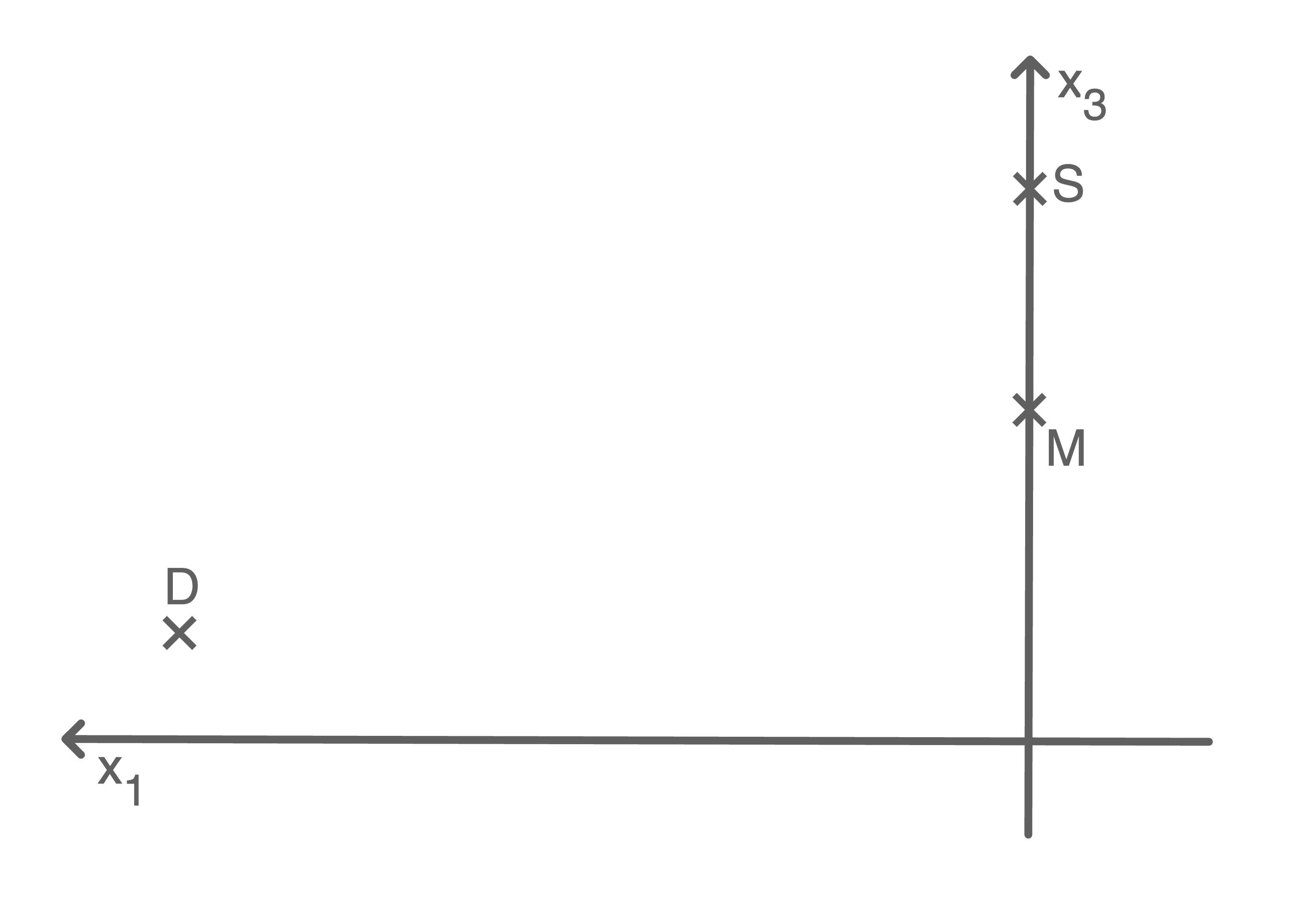
Lage begründen

Die Punkte $B, C, E$ und $F$ haben die $x_1$ -Koordinate 0.

Da die Punkte $B$ und $C$ Eckpunkte der Grundfläche sind und die Punkte $E$ und $F$ auf den Kanten der Pyramide liegen, folgt, dass $S$ ebenso die $x_1$ -Koordinate 0 besitzen muss und somit in der $x_2x_3$ -Ebene liegt.

Koordinaten berechnen

Gleichung einer Geraden aufstellen, die die Kante $\overline{AD}$ enthält:

$\begin{array}[t]{rll} g: \overrightarrow{x}&=& \overrightarrow{OA}+t\cdot \overrightarrow{AD} \\[5pt] &=& \pmatrix{10\\0\\0} +t\cdot \pmatrix{-2\\0\\1} \end{array}$

Da $S$ die $x_1$ Koordinate 0 besitzt, gilt:

$\pmatrix{0\\x_2\\x_3} = \pmatrix{10\\0\\0} +t\cdot \pmatrix{-2\\0\\1}$

Aus der ersten Zeile folgt:

$\begin{array}[t]{rll} 0&=& 10-2t &\quad \scriptsize \mid\; -10 \\[5pt] -10&=& -2t &\quad \scriptsize \mid\; :(-2) \\[5pt] 5 &=& t \end{array}$

Einsetzen von $t=5$ in die Geradengleichung liefert nun:

$\begin{array}[t]{rll} \overrightarrow{OS}&=& \pmatrix{10\\0\\0} +5\cdot \pmatrix{-2\\0\\1} & \\[5pt] &=& \pmatrix{0\\0\\5} \end{array}$

Die Koordinaten von $S$ sind somit gegeben durch $S(0\mid 0\mid 5).$

$L$ ist nicht parallel zur $x_1 x_2$ -Ebene.

Der Abstand von $S$ zu $L$ ist folglich kleiner als der Abstand von $S$ zu $M.$

Da der Abstand von $S$ zu $M$ genau 2 beträgt, folgt, dass der Abstand von $S$ zu $L$ kleiner als 2 ist.

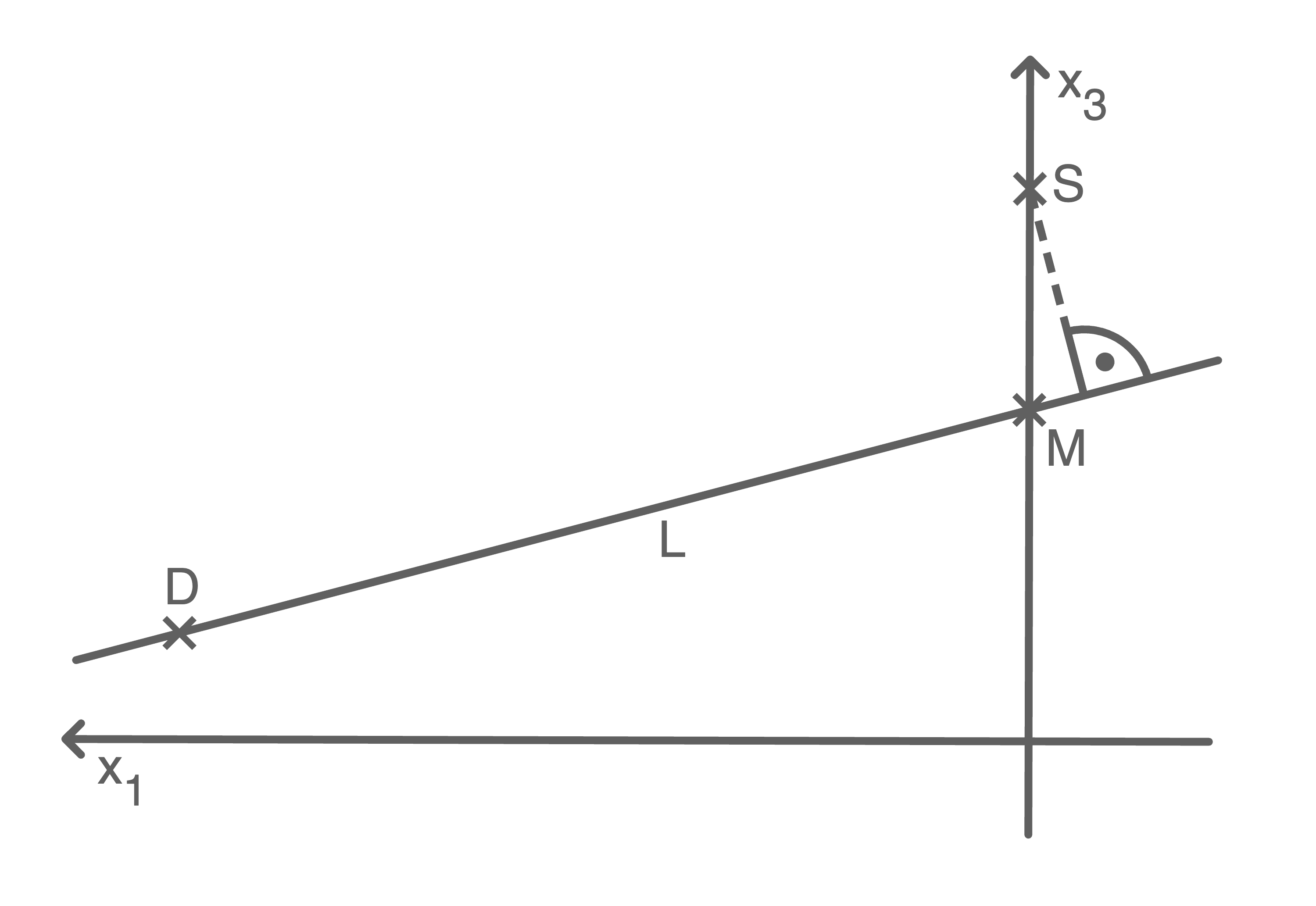
Skizze Abstand Ebene L Niedersachsen Mathe Abi 2023

Begründung

Das Dreieck $E F S$ stellt die Grundfläche der Pyramide dar.

Die Höhe der Pyramide ist gegeben durch den Abstand der Grundfläche zu der Spitze der Pyramide $D_t.$
Da die Grundfläche in der $x_2 x_3$ -Ebene liegt, entspricht der Abstand der $x_1$ -Koordinate von $D_t.$

Vorgehen beschreiben

Das Volumen des Körpers $A B C D_t E F$ kann berechnet werden, indem das Volumen der Pyramide $E F S D_t$ vom Volumen der Pyramide $A B C S$ subtrahiert wird.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?