Aufgabe 2B

Die Abbildung 1 zeigt das Netz eines Würfels.

Der Würfel wird 30-mal geworfen.

Die Zufallsgröße $X$ gibt an, wie oft die Zahl „4“ erzielt wird.

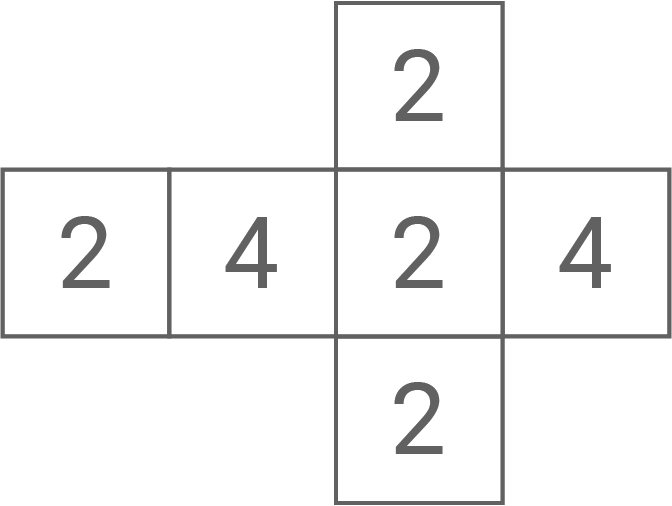
Abbildung 1

Begründe, dass $X$ binomialverteilt mit dem Parameter $p=\dfrac{1}{3}$ ist.

(3 BE)

Ermittle die Wahrscheinlichkeit dafür, dass die Zahl „4" häufiger erzielt wird als die Zahl „2“.

(3 BE)

Bestimme das kleinstmögliche zum Erwartungswert symmetrische Intervall, in dem die Anzahl der Würfe, in denen eine „4" erzielt wird, mit einer Wahrscheinlichkeit von mindestens $80 \,\%$ liegt.

(3 BE)

Gib im Sachzusammenhang ein Ereignis an, dessen Wahrscheinlichkeit mit dem Term $\pmatrix{29\\8}\cdot \left(\dfrac{1}{3}\right)^8\cdot \left(\dfrac{2}{3}\right)^{21}\cdot \dfrac{1}{3}$ berechnet werden kann.

(2 BE)

Bei einem Spiel mit diesem Würfel werfen zwei Personen abwechselnd. Das Spiel ist beendet, wenn eine Person eine andere Zahl würfelt als die andere Person direkt vorher.

Es gewinnt die Person, die in ihrem letzten Wurf die größere Zahl hat.

Eine der beiden Personen beginnt das Spiel.

Berechne die Wahrscheinlichkeit dafür, dass diese Person verliert und der Würfel insgesamt höchstens viermal geworfen wird.

(5 BE)

Die Abbildung 2 zeigt das Netz eines weiteren Würfels.

Der Würfel wird 7500-mal geworfen. Bei den ersten 1500 Würfen wird 285-mal die Zahl „6“ erzielt.

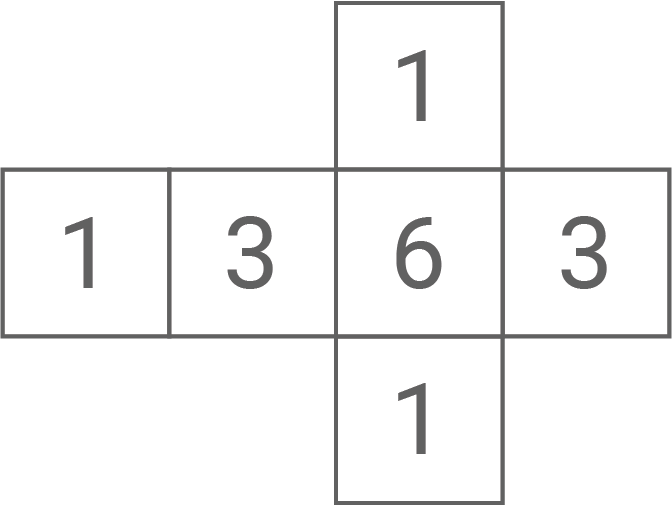
Abbildung 2

Ermittle die Wahrscheinlichkeit dafür, dass bei höchstens $17 \,\%$ der insgesamt 7500 Würfe die Zahl „6“ erzielt wird.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Da immer der gleiche Würfel geworfen wird und die Versuche unabhängig voneinander sind, bleibt die Wahrscheinlichkeit $p$ , eine „4“ zu erzielen, stets konstant.

Durch das 30-fache Würfeln ist eine feste Anzahl an Versuchen $n$ gegeben, bei denen jeweils zwei Ergebnisse - „Es wird eine „4“ erzielt“ und „Es wird keine „4“ erzielt“ - unterschieden werden.

Somit sind alle Bedingungen für eine Binomialverteilung erfüllt.

Da $X$ angibt, wie oft die Zahl „4“ erzielt wird, und zwei der sechs Würfelflächen mit einer „4“ beschriftet sind, folgt der Parameter $p$ mit $p=\dfrac{2}{6}=\dfrac{1}{3}.$

$X$ kann als binomialverteilt mit den Parametern $p=\dfrac{1}{3}$ und $n=30$ angenommen werden.

Die Zahl „4“ muss mindestens 16-mal fallen, sodass sie häufiger als die Zahl „2“ erzielt wird.

Es gilt:

$\begin{array}[t]{rll} P(X\geq 16)&=& 1-P(X \leq 15)& \quad \scriptsize \mid GTR \\[5pt] &\approx& 1- 0,981& \\[5pt] &=& 0,019 \end{array}$

Mit einer Wahrscheinlichkeit von etwa $1,9\,\%$ wird somit die Zahl „4“ häufiger erzielt als die Zahl „2“.

Erwartungswert $\mu$ berechnen:

$\mu=n\cdot p =30\cdot \dfrac{1}{3}=10$

Es soll gelten:

$P(\mu -c \leq X \leq \mu +c) \geq 0,8$

Systematisches Ausprobieren mit dem GTR liefert:

$c=2: \; P(8 \leq X \leq 12) \approx 67 \,\%$

$c=3: \; P(7 \leq X \leq 13) \approx 83 \,\%$

Das kleinstmögliche Intervall, das die geforderte Bedingung erfüllt, ist somit gegeben durch $[7 ; 13].$

Beim 30. Wurf wird zum neunten Mal die Zahl „4“ erzielt.

Hinweis: Es kann auch ein anderer als der letzte Wurf gesondert betrachtet werden.

Die Person, die das Spiel beginnt, verliert das Spiel mit höchstens vier Würfen, wenn abwechselnd folgende Zahlen gewürfelt werden:

$(2,4), (2,2,2,4), (4,4,2)$

Die Wahrscheinlichkeiten hierfür betragen:

$\begin{array}[t]{rll} P(2,4)&=& \dfrac{2}{3}\cdot \dfrac{1}{3} & \\[5pt] &=& \dfrac{2}{9} \end{array}$

$\begin{array}[t]{rll} P(2,2,2,4)&=& \left(\dfrac{2}{3}\right)^3\cdot \dfrac{1}{3} & \\[5pt] &=& \dfrac{8}{81} \end{array}$

$\begin{array}[t]{rll} P(4,4,2)&=& \left(\dfrac{1}{3}\right)^2\cdot \dfrac{2}{3} & \\[5pt] &=& \dfrac{2}{27} \end{array}$

Insgesamt gilt also:

$\begin{array}[t]{rll} P(\text{Spieler 1 verliert})&=& \dfrac{2}{9}+\dfrac{8}{81}+\dfrac{2}{27}&\\[5pt] &\approx & 0,395 \end{array}$

Die Person, die das Spiel beginnt, verliert folglich mit einer Wahrscheinlichkeit von $39,5\,\%$ nach höchstens vier Würfen.

Es gilt:

$0,17\cdot 7500=1275$

Da bei den ersten 1500 Würfen bereits 285-mal die Zahl „6“ erzielt wurde, folgt, dass von den weiteren 6000 Würfen bei höchstens $1275-285=990$ Würfen eine „6“ erzielt werden soll.

$Y$ beschreibt die Anzahl der Würfe, bei denen die Zahl „6“ erzielt wird, und kann als binomialverteilt mit den Parametern $p=\dfrac{1}{6}$ und $n=6000$ angenommen werden.

Die Wahrscheinlichkeit, dass bei höchstens 990 Würfen die Zahl „6“ erzielt wird, folgt also mit:

$P(Y\leq 990) \approx 0,37$

Mit einer Wahrscheinlichkeit von etwa $37\,\%$ wird somit bei höchstens $17 \,\%$ der 7500 Würfe die Zahl „6“ erzielt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?