Pflichtteil 1

Aufgabe P1

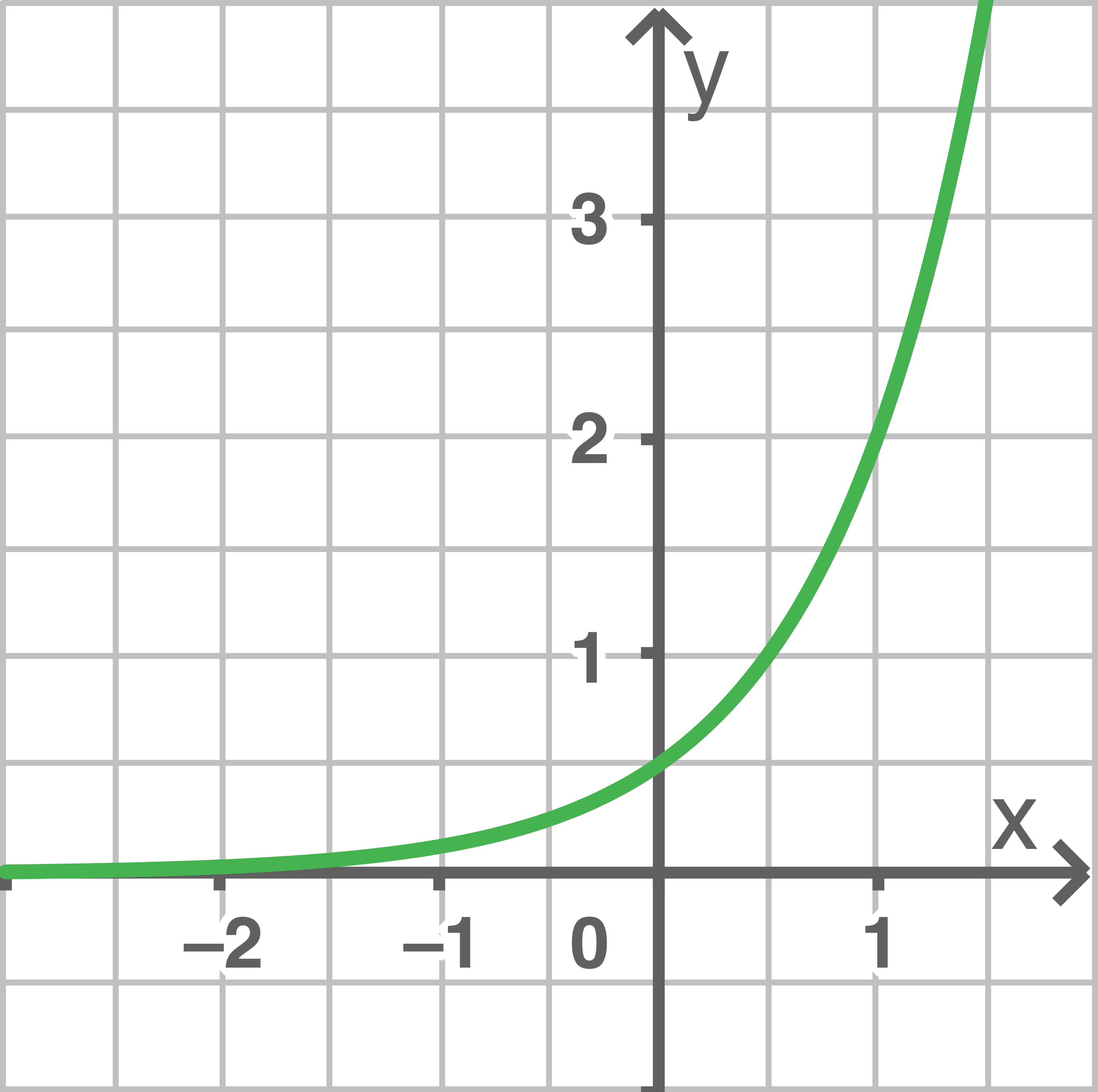
Die Abbildung zeigt den Graphen der Funktion $f$ mit $f(x)=a \cdot b^{x}$ mit $a>0$ und $b>0$ . Bestimme die passenden Werte von $a$ und $b$ .

ni abi gk gtr cas 2022 pflichtteil 1 abbildung 1

(3 BE)

Der Graph der in $\mathbb{R}$ definierten Funktion $g$ mit $g(x)=3^{x}$ wird um 2 in negative $x$ -Richtung verschoben.
Zeige, dass der dadurch entstehende Graph auch durch eine Streckung des Graphen von $g$ in $y$ -Richtung erzeugt werden kann.

(2 BE)

Aufgabe P2

Eine ganzrationale Funktion $f$ hat die Nullstellen $1,$ $2$ und $-3.$
Gib eine Funktionsgleichung für $f$ an.

(2 BE)

Für eine Funktion $h$ gilt: $h^{\prime}(x)=x^{2}-2 x-24$
Bestimme die Extremstellen des Graphen von $h.$

(3 BE)

Aufgabe P3

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=x^{2}.$
Bestimme diejenige reelle Zahl $m$ mit $m\lt 0,$ für die der Graph von $f$ und die Gerade mit der Gleichung $y=m \cdot x$ eine Fläche mit dem Inhalt $36$ einschließen.

(5 BE)

Aufgabe P4

Gegeben sind die Punkte $A(0\mid 0\mid 0),$ $B(8\mid 6\mid 0)$ und $C(4\mid 3\mid z),$ wobei $z$ eine positive reelle Zahl ist.

Zeige, dass es sich bei dem Dreieck $A B C$ um ein gleichschenkliges Dreieck mit der Basis $\overline{A B}$ handelt.

(2 BE)

Das Dreieck $A B C$ hat den Flächeninhalt $35 .$ Bestimme den Wert von $z$ .

(3 BE)

Aufgabe P5

Gegeben sind die Punkte $P(2\mid0\mid 1)$ und $Q(2\mid4\mid9)$ sowie die parallelen Geraden
$g: \vec{x}=\overrightarrow{O P}+s \cdot\left(\begin{array}{c}3 \\ -1 \\ 2\end{array}\right)$ und $h: \vec{x}=\overrightarrow{O Q}+t \cdot\left(\begin{array}{c}3 \\ -1 \\ 2\end{array}\right)$ mit $s, t \in \mathbb{R}.$

Zeige, dass $g$ und $h$ nicht identisch sind.

(2 BE)

Bestimme eine Gleichung der Gerade, die parallel zu $g$ und $h$ ist und die Strecke $\overline{P Q}$ im Punkt $T$ schneidet, wobei $3 \cdot|\overline{P T}|=|\overline{Q T}|$ ist.

(3 BE)