Aufgabe 3A
Ein Element eines Klettergartens ist eine ebene, viereckige Kletterwand. In einem Koordinatensystem können die Eckpunkte der Kletterwand durch die Punkte 
und 
beschrieben werden.
Die
-Ebene stellt den horizontalen Boden dar. Die Kletterwand liegt in einer Ebene, die senkrecht zur -Ebene steht. Eine Längeneinheit im Koordinatensystem entspricht 1 Meter (m) in der Wirklichkeit.
hohen Masten gespannt ist. Der Fußpunkt des ersten Masts wird durch 
dargestellt, der Fußpunkt des zweiten Masts durch 
Das Seil ist am ersten Mast in einer Höhe von 
befestigt, am zweiten Mast in einer Höhe von 
Es soll davon ausgegangen werden, dass das Seil geradlinig verläuft.
Die
a)
Weise nach, dass die Kletterwand die Form eines Parallelogramms hat, aber nicht rechteckig ist.
(4 BE)
b)
Auf der Kletterwand verläuft eine horizontale Linie, die den Punkt 
enthält. Diese Linie teilt die Wand in zwei Teile.
Begründe, dass der Flächeninhalt des unteren Teils größer ist als der des oberen Teils.
Ein anderes Element des Klettergartens ist ein Stahlseil, das zwischen zwei vertikal stehenden, Begründe, dass der Flächeninhalt des unteren Teils größer ist als der des oberen Teils.
(4 BE)
c)
Stelle die beiden Masten und das Seil in einem dreidimensionalen Koordinatensystem dar.
(3 BE)
d)
Bestimme die Neigung des Seils zwischen den beiden Masten in Prozent.
(4 BE)
e)
Über das bisher betrachtete Seil hinweg ist ein zweites Stahlseil gespannt. Dieses obere Seil verläuft entlang der Geraden 
mit 
Ein Punkt des oberen Seils liegt vertikal über einem Punkt des unteren Seils.
Ermittle den Abstand dieser beiden Punkte.
Ermittle den Abstand dieser beiden Punkte.
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Zu prüfen ist ob die gegenüberliegenden Seiten gleich lang und parallel sind.
Also sind gegenüberliegende Seiten parallel und gleich lang.
Überprüfen ob die Kletterwand rechteckig ist:
Also ist kein rechter Winkel im Eckpunkt 
.
b)
Eine gedachte gerade Linie zwischen den durch und 
dargestellten Eckpunkten der Kletterwand teilt diese in zwei Teile mit gleichem Flächeninhalt. Da die 
-Koordinate von größer ist als die von , verläuft die horizontale Linie oberhalb der gedachten Linie. Folglich ist der Flächeninhalt des unteren Teils größer als der des oberen Teils.
c)
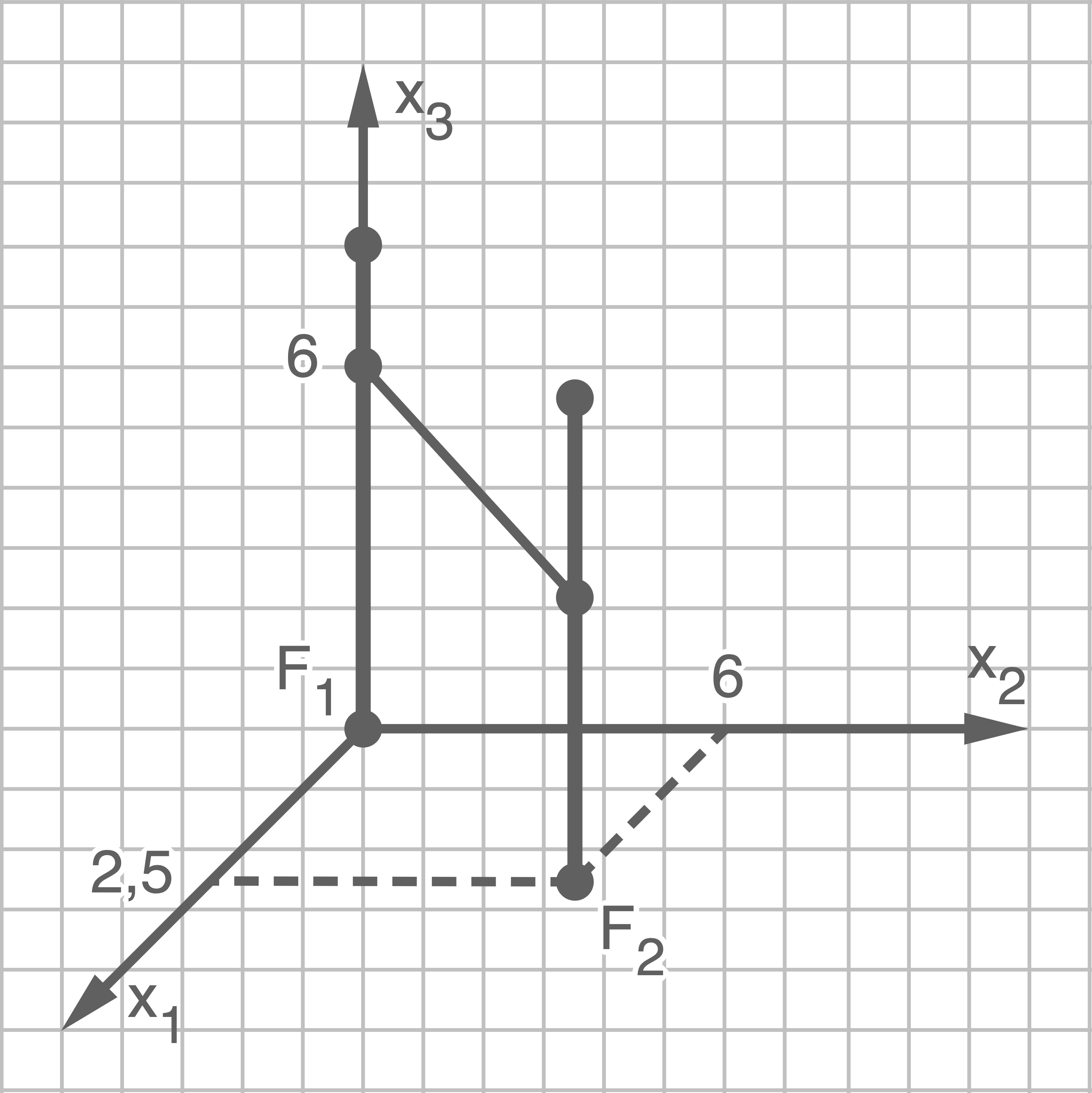
d)
Das Seil ist 
lang.
Mit den Befestigungshöhen und der Länge des Seils wird die Neigung bestimmt.
Die Neigung des Seils beträgt somit 
e)
Die Gerade, mit deren Hilfe sich das untere Seil beschreiben lässt, kann durch die Gleichung 
mit 
dargestellt werden.
Da die beiden beschriebenen Punkte die gleiche 
-Koordinate haben, gilt 
, daraus folgt 
Der untere Punkt liegt also in einer Höhe von 
Das obere Seil verläuft horizontal in einer Höhe von 
, der gesuchte Abstand beträgt also 
.