Wahlaufgaben 2
Aufgabe R1
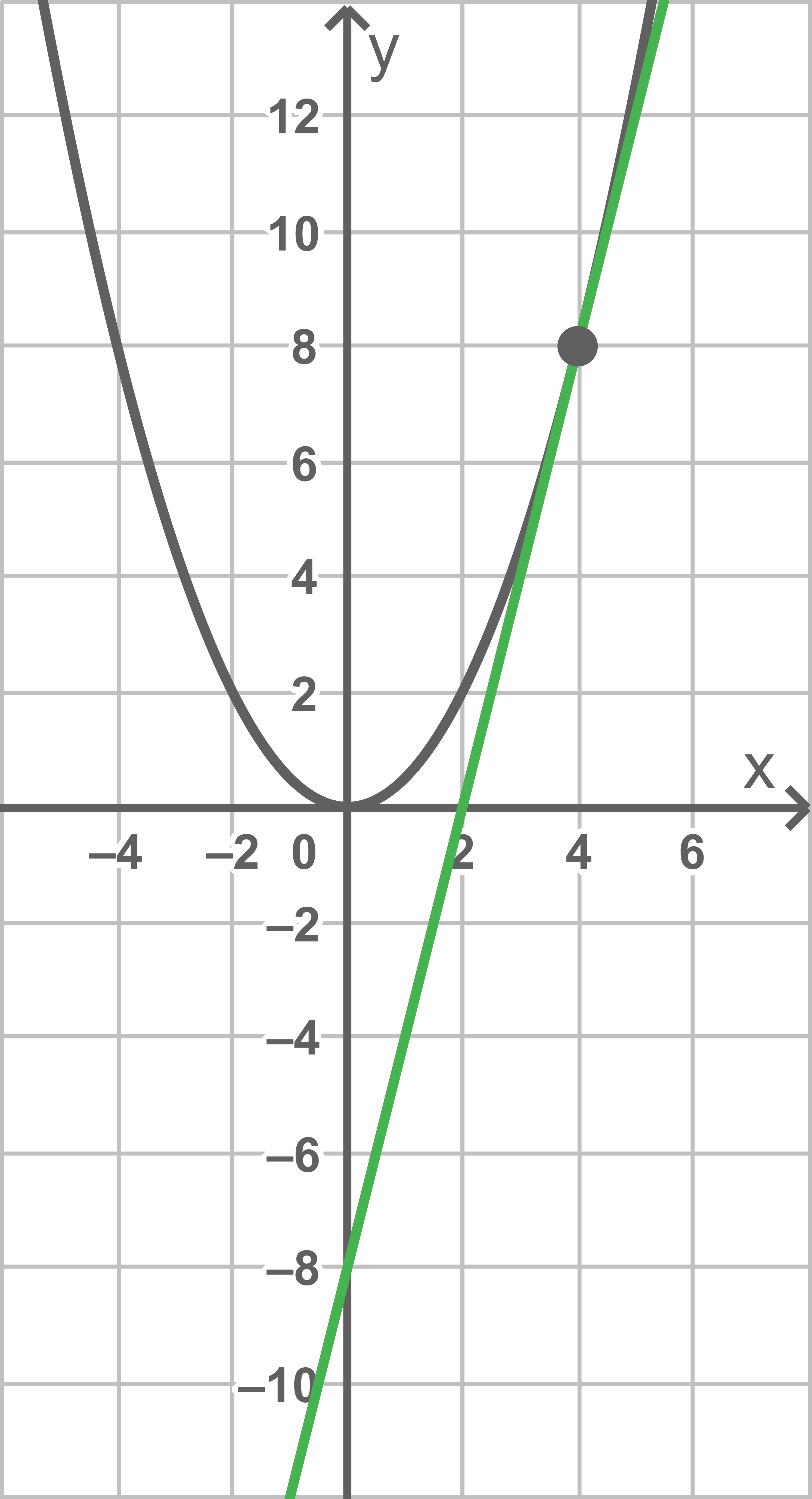
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  Die Abbildung zeigt den Graphen von
Die Abbildung zeigt den Graphen von  sowie die Tangente
sowie die Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt  .
.

a)
Gib anhand der Abbildung eine Gleichung der Tangente  an.
an.
(1 BE)
b)
Weise nach, dass für jeden Wert  die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt  die
die  -Achse im Punkt
-Achse im Punkt  schneidet.
schneidet.
(4 BE)
Aufgabe R2
In einem Betrieb werden Geräte hergestellt, von denen jedes mit einer Wahrscheinlichkeit von
a)
Zeige, dass die Wahrscheinlichkeit dafür, dass ein Gerät fehlerfrei ist und als fehlerfrei eingestuft wird,  beträgt.
beträgt.
(2 BE)
b)
Formuliere eine Aussage im Sachzusammenhang, die sich in Verbindung mit der Gleichung  aus der folgenden Ungleichung ergibt:
aus der folgenden Ungleichung ergibt:

(3 BE)
Aufgabe R3
Betrachtet wird das Quadrat, das folgende Eigenschaften besitzt:- Das Quadrat liegt in der
-Ebene.
- Ein Eckpunkt liegt im Koordinatenursprung.
- Der Schnittpunkt der Diagonalen des Quadrats liegt auf der Geraden
mit
, und auf der Geraden
mit
.
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung R1
a)
Die Tangente  gegeben durch die Gleichung
gegeben durch die Gleichung  hat eine positive Steigung, einen
hat eine positive Steigung, einen  -Achsenabschnitt von
-Achsenabschnitt von  und schneidet die
und schneidet die  -Achse bei
-Achse bei  Für die Steigung
Für die Steigung  folgt somit:
folgt somit:
 Somit ergibt sich die Gleichung
Somit ergibt sich die Gleichung 
b)
Die allgemeine Gleichung der Tangente ist gegeben durch  Für die Ableitung von
Für die Ableitung von  gilt:
gilt:
 Somit folgt
Somit folgt  und
und  Einsetzen der Koordinaten des Punktes
Einsetzen der Koordinaten des Punktes  an dem die Tangente den Graphen berührt, in die Gleichung der Tangente liefert somit:
an dem die Tangente den Graphen berührt, in die Gleichung der Tangente liefert somit:
![\(\begin{array}[t]{rll}
f(x)&=& u\cdot x + n &\quad \scriptsize \; \bigg \vert\, \; \left(u\mid \frac{1}{2}u^2\right) \\[5pt]
\dfrac{1}{2}u^2&=& u\cdot u + n &\quad \scriptsize \; \bigg \vert\, \;-u^2 \\[5pt]
-\dfrac{1}{2}u^2&=& n
\end{array}\)](https://mathjax.schullv.de/549df2afb21f53dcf073a2558c53d662a711129584a4df7e688378369f0d5db1?color=5a5a5a) Somit gilt
Somit gilt  und die Tangente schneidet die
und die Tangente schneidet die  -Achse damit im Punkt
-Achse damit im Punkt 
Lösung R2
a)
Aus der Aufgabenstellung folgt:
Wahrscheinlichkeit, dass ein Gerät fehlerfrei ist:  Wahrscheinlichkeit, dass ein fehlerfreies Gerät als fehlerfrei eingestuft wird:
Wahrscheinlichkeit, dass ein fehlerfreies Gerät als fehlerfrei eingestuft wird: 
b)
Die erste Gleichung beschreibt die Gesamtwahrscheinlichkeit, dass ein Gerät als fehlerfrei eingestuft wird, unabhängig davon, ob es tatsächlich fehlerfrei ist oder nicht.
Die zweite Gleichung beschreibt somit die Wahrscheinlichkeit, dass in einer Stichprobe von 100 Geräten mindestens 90 Geräte als fehlerfrei erkannt werden.
„Da ein kleiner Anteil fehlerhafter Geräte ebenfalls als fehlerfrei eingestuft wird, ist es wahrscheinlicher, dass mindestens  der Geräte aus der Stichprobe von 100 Geräten als fehlerfrei erkannt werden, als dass weniger als die erwarteten
der Geräte aus der Stichprobe von 100 Geräten als fehlerfrei erkannt werden, als dass weniger als die erwarteten  der Geräte als fehlerhaft eingestuft werden.“
Alternative Lösung:
"Mit einer Wahrscheinlichkeit von über
der Geräte als fehlerhaft eingestuft werden.“
Alternative Lösung:
"Mit einer Wahrscheinlichkeit von über  werden in einer Stichprobe von 100 Geräten mindestens 90 Geräte als fehlerfrei erkannt werden, da ein kleiner Anteil fehlerhafter Geräte ebenfalls als fehlerfrei eingestuft wird."
werden in einer Stichprobe von 100 Geräten mindestens 90 Geräte als fehlerfrei erkannt werden, da ein kleiner Anteil fehlerhafter Geräte ebenfalls als fehlerfrei eingestuft wird."