Aufgabe 1B
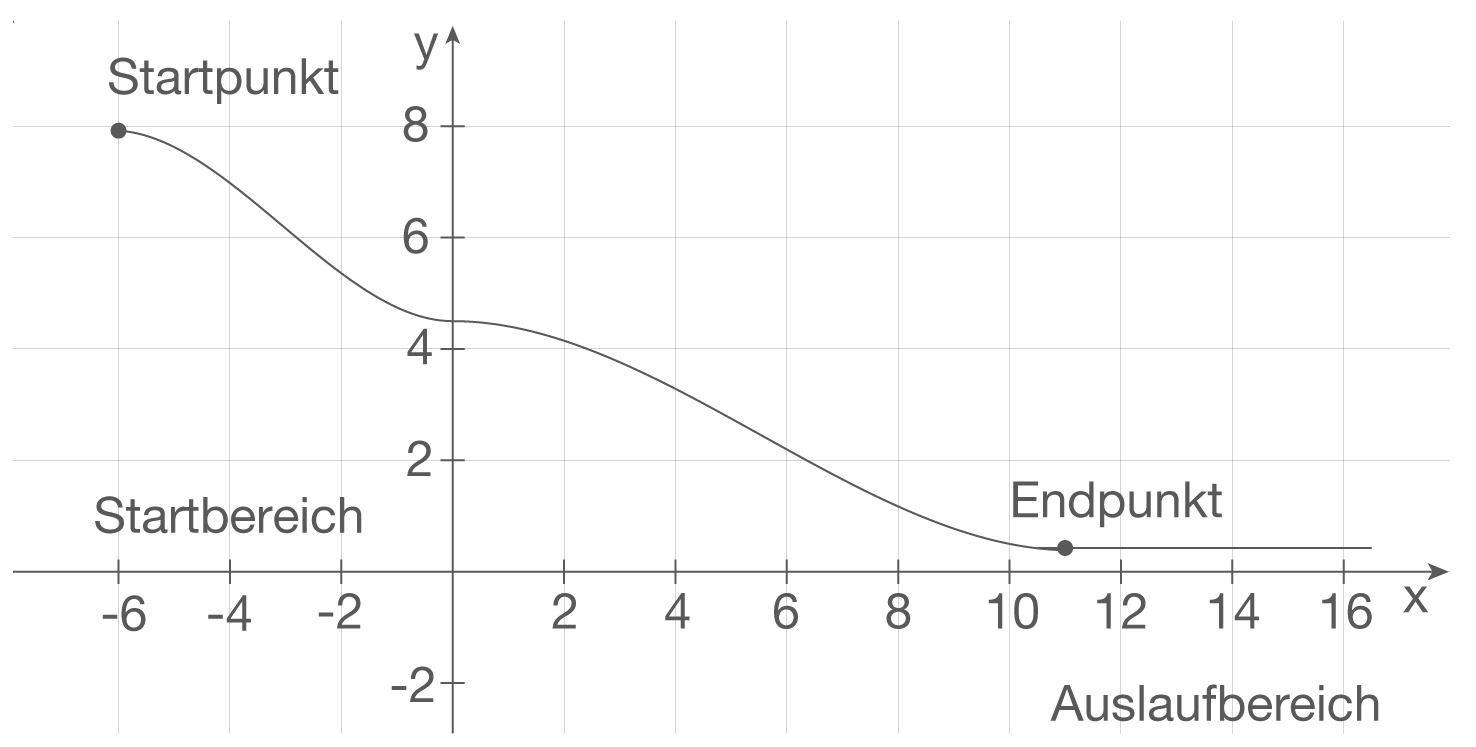
Die nebenstehende Abbildung stellt einen Entwurf für das Profil einer Wasserrutsche dar. Dabei wird für den Startbereich für  die Funktion
die Funktion  mit
mit
 und für
und für  die Funktion
die Funktion  mit
mit
 verwendet;
verwendet;  in Metern,
in Metern,  und
und  Höhe über dem Boden in Metern.
Höhe über dem Boden in Metern.
Der waagerechte Boden ist durch die -Achse gegeben.
-Achse gegeben.
Der waagerechte Boden ist durch die
a) Bestimmen Sie die Höhe der Rutsche am Startpunkt, die durchschnittliche Steigung im Startbereich und die betragsmäßig größte Steigung im Startbereich.
Weisen Sie nach, dass der Übergang zwischen der Modellierung mit und
und  sprung- und knickfrei ist.
sprung- und knickfrei ist.
Bestimmen Sie die Stelle, an der die Rutsche enden muss, damit sie knickfrei in einen waagerechten Auslaufbereich übergeht.
Weisen Sie nach, dass der Übergang zwischen der Modellierung mit
Bestimmen Sie die Stelle, an der die Rutsche enden muss, damit sie knickfrei in einen waagerechten Auslaufbereich übergeht.
(15P)
b) Rutscht der Badegast schnell genug, so berührt er nach dem Startbereich die Rutsche nicht mehr und fliegt ein Stück durch die Luft. Seine Flugbahn lässt sich vereinfacht beschreiben durch eine Funktion  mit
mit  ;
; 


 in Metern,
in Metern,  Höhe über dem Boden in Metern.
Höhe über dem Boden in Metern.
Bestimmen Sie so, dass der Badegast im Punkt
so, dass der Badegast im Punkt  wieder auf die Rutsche trifft.
wieder auf die Rutsche trifft.
 betragsmäßig um mehr als 0,1 von der Steigung der Rutsche an dieser Stelle unterscheidet.
betragsmäßig um mehr als 0,1 von der Steigung der Rutsche an dieser Stelle unterscheidet.
Bestimmen Sie
(Zur Kontrolle:  )
)
Untersuchen Sie, ob sich die Steigung seiner Flugbahn am Auftreffpunkt
(7P)
c) Die Seitenflächen der Rutsche sollen für  bis zum Boden verkleidet werden.
bis zum Boden verkleidet werden.
Berechnen Sie den Flächeninhalt einer der zu verkleidenden Seitenflächen.
einer der zu verkleidenden Seitenflächen.
Jede Seitenfläche soll in zwei Teilflächen zerlegt werden, die mit verschiedenen Materialien verkleidet werden.
Durch den Term (1)
 kann für
kann für 



 der Flächeninhalt einer Teilfläche berechnet werden.
der Flächeninhalt einer Teilfläche berechnet werden.
Erläutern Sie die diesem Term zugrundeliegende Zerlegung auch mithilfe einer Skizze in der Abbildung 1 der Anlage für einen geeigneten Wert .
.
Eine andere Zerlegung der Seitenfläche ergibt sich aus der Gleichung (2)
 .
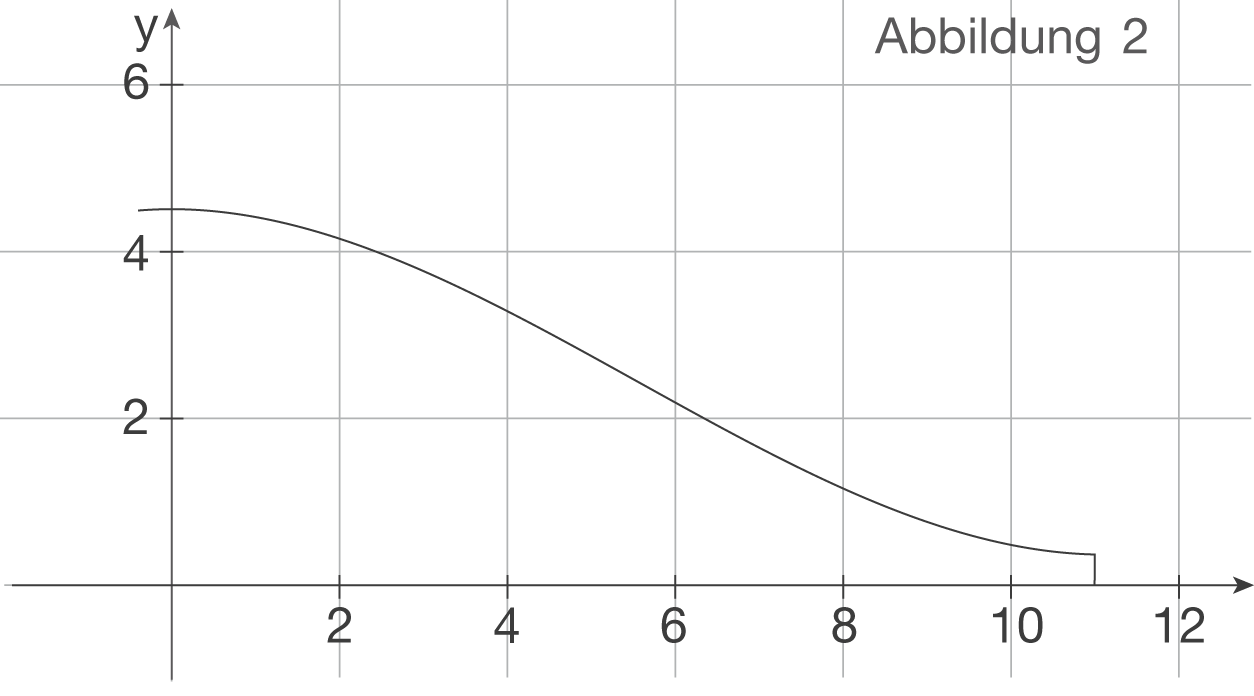
Erläutern Sie die dieser Gleichung zugrundeliegende Zerlegung auch mithilfe einer Skizze in der Abbildung 2 der Anlage.
.
Erläutern Sie die dieser Gleichung zugrundeliegende Zerlegung auch mithilfe einer Skizze in der Abbildung 2 der Anlage.
Berechnen Sie den Flächeninhalt
Jede Seitenfläche soll in zwei Teilflächen zerlegt werden, die mit verschiedenen Materialien verkleidet werden.
Durch den Term (1)
Erläutern Sie die diesem Term zugrundeliegende Zerlegung auch mithilfe einer Skizze in der Abbildung 1 der Anlage für einen geeigneten Wert
Eine andere Zerlegung der Seitenfläche ergibt sich aus der Gleichung (2)
(12P)
(34P)
Material
Anlage: Abbildungen zu Teilaufgabe c)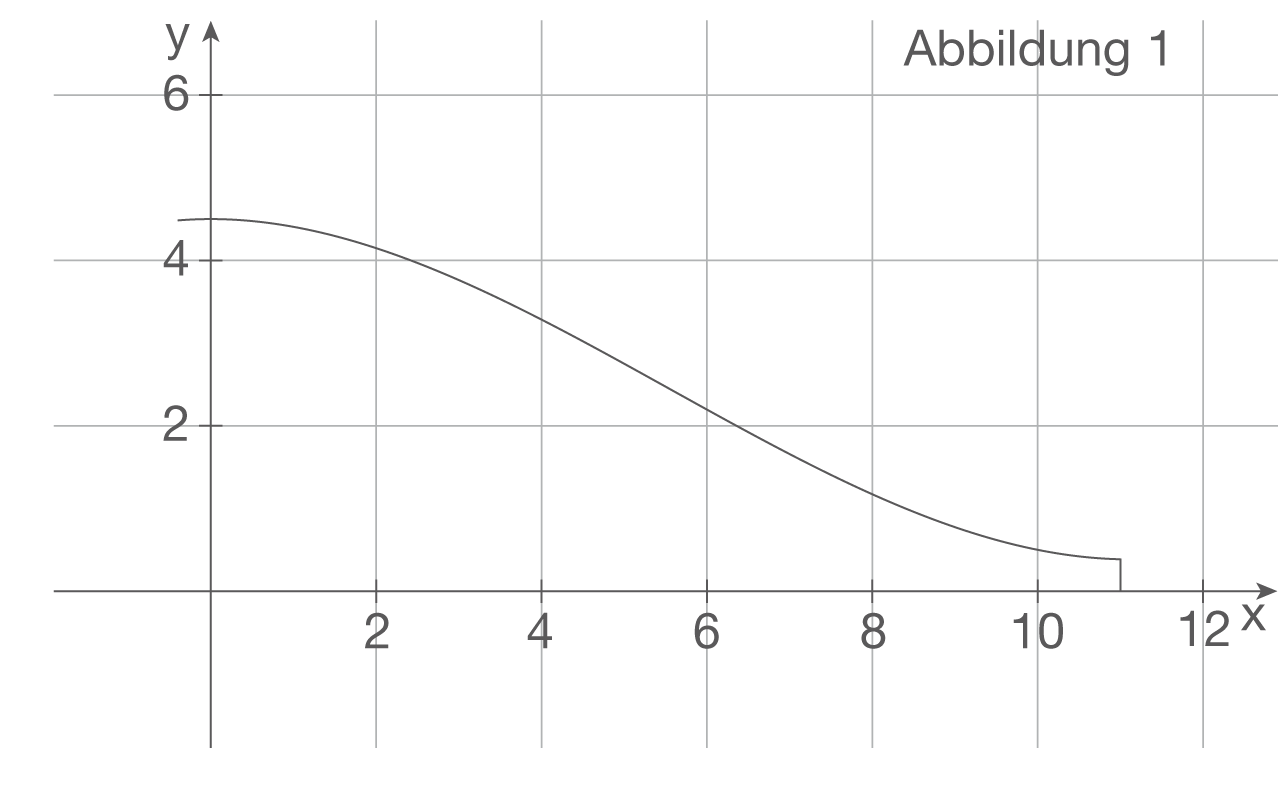
Für den Verlauf einer Rutsche werden für  die Funktion
die Funktion  mit
mit  und für
und für  die Funktion
die Funktion  mit
mit  verwendet;
verwendet;  in Metern,
in Metern,  und
und  Höhe über dem Boden in Metern. Der waagerechte Boden ist durch die
Höhe über dem Boden in Metern. Der waagerechte Boden ist durch die  -Achse gegeben.
-Achse gegeben.
a)  Höhe der Rutsche am Startpunkt
Du sollst die Höhe der Rutsche am Startpunkt bestimmen. Dafür berechnest du
Höhe der Rutsche am Startpunkt
Du sollst die Höhe der Rutsche am Startpunkt bestimmen. Dafür berechnest du  , da die Funktion
, da die Funktion  den Startbereich der Rutsche modelliert und der Startpunkt bei
den Startbereich der Rutsche modelliert und der Startpunkt bei  liegt.
liegt.
 Die Höhe im Startpunkt der Rutsche beträgt
Die Höhe im Startpunkt der Rutsche beträgt  .
.
 Durchschnittliche Steigung im Startbereich
Um die durchschnittliche Steigung im Startbereich zu berechnen, benötigst du die mittlere Änderungsrate:
Durchschnittliche Steigung im Startbereich
Um die durchschnittliche Steigung im Startbereich zu berechnen, benötigst du die mittlere Änderungsrate:
 Der Startbereich beginnt bei
Der Startbereich beginnt bei  und endet bei
und endet bei  . Berechne also mit diesen Werten und der Formel für die mittlere Änderungsrate die gesuchte durchschnittliche Steigung:
. Berechne also mit diesen Werten und der Formel für die mittlere Änderungsrate die gesuchte durchschnittliche Steigung:
![\(\begin{array}{rll}
\Delta m&=&\dfrac{f(0) - f(-6)}{0 - (-6)} \\[5pt]
&=&\dfrac{4,5 - 7,92}{0 +6} \\[5pt]
&=&\dfrac{-3,42}{6} \\[5pt]
&=& -0,57 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/b3fa078f3869c2a205013abbb97c8d45393689a7450d951f125406f2b3e18ab3?color=5a5a5a) Die durchschnittliche Steigung im Startbereich beträgt somit
Die durchschnittliche Steigung im Startbereich beträgt somit 
 Betragsmäßig größte Steigung im Startbereich
Außerdem sollst du die betragsmäßig größte Steigung im Startbereich berechnen. Die Ableitung der Funktion
Betragsmäßig größte Steigung im Startbereich
Außerdem sollst du die betragsmäßig größte Steigung im Startbereich berechnen. Die Ableitung der Funktion  beschreibt die Steigung im Startbereich. Da
beschreibt die Steigung im Startbereich. Da  auf dem Bereich
auf dem Bereich  monoton fällt (Steigung negativ), ist die betragsmäßig größte Steigung das Minimum der Ableitung von
monoton fällt (Steigung negativ), ist die betragsmäßig größte Steigung das Minimum der Ableitung von  . Berechne also zunächst die ersten 3 Ableitungen von
. Berechne also zunächst die ersten 3 Ableitungen von  :
:
![\(\begin{array}{rll}
f(x)&=&0,03\cdot x^3 + 0,275 \cdot x^2 + 4,5\\[5pt]
f‘(x)&=&0,09\cdot x^2 + 0,55 \cdot x\\[5pt]
f‘‘(x)&=&0,18\cdot x + 0,55\\[5pt]
f‘‘‘(x)&=&0,18\\[5pt]
\end{array}\)](https://mathjax.schullv.de/9d4538b7f93a38a142ddf258a178b4ecc9905d5c136499a832cb2d6432cee44d?color=5a5a5a) Um das Minimum der 1. Ableitung zu bestimmen, musst du die Nullstelle der 2. Ableitung berechnen:
Um das Minimum der 1. Ableitung zu bestimmen, musst du die Nullstelle der 2. Ableitung berechnen:
![\(\begin{array}{rll}
f‘‘(x)&=&0\\[5pt]
0&=&0,18\cdot x + 0,55&\scriptsize \mid\; -0,55\\[5pt]
-0,55&=&0,18 \cdot x&\scriptsize \mid\; :0,18\\[5pt]
x &=& -3,056
\end{array}\)](https://mathjax.schullv.de/2e33cee57d99dce9684f1465f7ed4f3e958697a7be1050b120147bf5ad51213f?color=5a5a5a) Die Nullstelle der 2. Ableitung ist gegeben durch
Die Nullstelle der 2. Ableitung ist gegeben durch  . Es handelt sich tatsächlich um ein Minimum, da die 3. Ableitung an der Stelle
. Es handelt sich tatsächlich um ein Minimum, da die 3. Ableitung an der Stelle  positiv ist:
positiv ist:
 Um die betragsmäßig größte Steigung zu berechnen, setze nun
Um die betragsmäßig größte Steigung zu berechnen, setze nun  in die 1. Ableitung ein:
in die 1. Ableitung ein:
 Die betragsmäßig größte Steigung ist somit gegeben durch
Die betragsmäßig größte Steigung ist somit gegeben durch  .
.
 Übergang zwischen
Übergang zwischen  und
und  Du sollst nachweisen, dass der Übergang zwischen der Modellierung mit
Du sollst nachweisen, dass der Übergang zwischen der Modellierung mit  und
und  sprung- und knickfrei ist. Dafür müssen zwei Bedingungen erfüllt sein:
sprung- und knickfrei ist. Dafür müssen zwei Bedingungen erfüllt sein:
 hast du bereits berechnet. Berechne also noch die Ableitung von
hast du bereits berechnet. Berechne also noch die Ableitung von  .
.
 Überprüfe nun die beiden Bedingungen.
Überprüfe nun die beiden Bedingungen.
 Da beide Bedingungen erfüllt sind, verläuft der Übergang zwischen der Modellierung von
Da beide Bedingungen erfüllt sind, verläuft der Übergang zwischen der Modellierung von  und
und  sprung- und knickfrei.
sprung- und knickfrei.
 Knickfreier Übergang in Auslaufbereich der Rutsche
Du sollst die Stelle berechnen, an der die Rutsche enden muss, damit sie knickfrei in einen waagerechten Auslaufbereich übergeht. Das heißt die Steigung muss übereinstimmen. Eine waagrechte Strecke hat eine Steigung von
Knickfreier Übergang in Auslaufbereich der Rutsche
Du sollst die Stelle berechnen, an der die Rutsche enden muss, damit sie knickfrei in einen waagerechten Auslaufbereich übergeht. Das heißt die Steigung muss übereinstimmen. Eine waagrechte Strecke hat eine Steigung von  , somit muss auch die Funktion
, somit muss auch die Funktion  eine Steigung von
eine Steigung von  haben. Berechne also
haben. Berechne also  , um die gesuchte Übergangsstelle zu berechnen:
, um die gesuchte Übergangsstelle zu berechnen:
![\(\begin{array}{rll}
0&=&g‘(x)& \\
0&=&0,018\cdot x^2 - 0,2\cdot x&\scriptsize (x \text{ ausklammern}) \\[5pt]
0&=&(0,018\cdot x - 0,2)\cdot x&\scriptsize (x_1 = 0) \\[5pt]
0&=&0,018\cdot x - 0,2&\scriptsize \mid\; +0,2\\[5pt]
0,2&=&0,018\cdot x&\scriptsize \mid\; :0,018\\[5pt]
x_2&=&11,11&
\end{array}\)](https://mathjax.schullv.de/a438fea3ab3fc001daff4d9761eb51dbf2534d83837da3c54ea9cd2eefe2303d?color=5a5a5a) Die Stelle, an der die Rutsche knickfrei in einen waagrechten Auslaufbereich übergeht, ist gegeben durch
Die Stelle, an der die Rutsche knickfrei in einen waagrechten Auslaufbereich übergeht, ist gegeben durch  .
.
(Vermeidung des Sprungs)
(Vermeidung des Knicks)
b)  Funktion der Flugbahn berechnen
Rutscht der Badegast schnell genug, so berührt er nach dem Startbereich die Rutsche nicht mehr und fliegt ein Stück durch die Luft. Seine Flugbahn lässt sich vereinfacht beschreiben durch eine Funktion
Funktion der Flugbahn berechnen
Rutscht der Badegast schnell genug, so berührt er nach dem Startbereich die Rutsche nicht mehr und fliegt ein Stück durch die Luft. Seine Flugbahn lässt sich vereinfacht beschreiben durch eine Funktion  mit
mit  ;
; 
 ;
; 
 in Metern,
in Metern,  Höhe über dem Boden in Metern.
Höhe über dem Boden in Metern.
Du sollst so berechnen, dass der Badegast im Punkt
so berechnen, dass der Badegast im Punkt  wieder auf die Rutsche trifft. Der Badegast trifft also auf die Funktion
wieder auf die Rutsche trifft. Der Badegast trifft also auf die Funktion  . Der Graph der Funktion
. Der Graph der Funktion  und der Graph der Funktion
und der Graph der Funktion  müssen dann an der Stelle
müssen dann an der Stelle  , an der der Badegast wieder auf die Rutsche trifft, die gleiche Höhe haben. Es gilt also:
, an der der Badegast wieder auf die Rutsche trifft, die gleiche Höhe haben. Es gilt also:
 Der Punkt
Der Punkt  hat dann folgende Form
hat dann folgende Form  .
.
Durch Einsetzen des Punktes in
in  kannst du den Parameter
kannst du den Parameter  berechnen:
berechnen:
![\(\begin{array}{rll}
p(5)&=&a\cdot 5^2 + 4,5&\\[5pt]
2,75&=&a\cdot 25 + 4,5&\scriptsize \mid\; -4,5\\[5pt]
-1,75&=&a\cdot 25 &\scriptsize \mid\; :25\\[5pt]
a&=&-0,07 &\scriptsize \mid\; :25\\[5pt]
\end{array}\)](https://mathjax.schullv.de/b1a30250cfa73bba6d959abb39c172a8dae58ce9562b851db73b304ba4fd54a6?color=5a5a5a) Die Flugbahn des Badegasts wird modelliert durch
Die Flugbahn des Badegasts wird modelliert durch  .
.
 Vergleich der Steigungen von Flugbahn und Rutsche im Auftreffpunkt
Du sollst untersuchen, ob sich die Steigung der Flugbahn des Badegasts am Auftreffpunkt
Vergleich der Steigungen von Flugbahn und Rutsche im Auftreffpunkt
Du sollst untersuchen, ob sich die Steigung der Flugbahn des Badegasts am Auftreffpunkt  betragsmäßig um mehr als 0,1 von der Steigung der Rutsche an dieser Stelle unterscheidet. Berechne dafür zunächst die Ableitung von
betragsmäßig um mehr als 0,1 von der Steigung der Rutsche an dieser Stelle unterscheidet. Berechne dafür zunächst die Ableitung von  , die Ableitung von
, die Ableitung von  hast du bereits etwas früher in dieser Aufgabe berechnet.
hast du bereits etwas früher in dieser Aufgabe berechnet.
 Berechne nun die Steigung an der Stelle
Berechne nun die Steigung an der Stelle  für beide Funktionen:
für beide Funktionen:
 Berechne nun die Steigungsdifferenz:
Berechne nun die Steigungsdifferenz:
 Der Steigungsunterschied ist größer als 0,1.
Der Steigungsunterschied ist größer als 0,1.
Du sollst
Durch Einsetzen des Punktes
c)  Flächeninhalt der Seitenfläche berechnen
Die Seitenflächen der Rutsche sollen für
Flächeninhalt der Seitenfläche berechnen
Die Seitenflächen der Rutsche sollen für  bis zum Boden verkleidet werden. Du sollst nun den Flächeninhalt
bis zum Boden verkleidet werden. Du sollst nun den Flächeninhalt  einer der zu verkleidenden Seitenflächen berechnen. Es ist also der Wert des folgenden Integrals gesucht:
einer der zu verkleidenden Seitenflächen berechnen. Es ist also der Wert des folgenden Integrals gesucht:
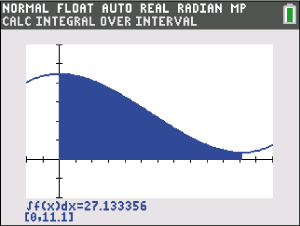
 Das Integral kannst du mithilfe deines Graphiktaschenrechners lösen. Zeichne dazu den Graphen der Funktion
Das Integral kannst du mithilfe deines Graphiktaschenrechners lösen. Zeichne dazu den Graphen der Funktion  und nutze die Integralfunktion aus dem CALC-Menü.
und nutze die Integralfunktion aus dem CALC-Menü.
 Alternativ
Alternativ
Du kannst das Integral jedoch auch von Hand berechnen:![\(\begin{array}{rll}
\displaystyle\int_{0}^{11,1} g(x) \mathrm{dx}&=&\displaystyle\int_{0}^{11,1} (0,006\cdot x^3 - 0,1\cdot x^2 +4,5) \mathrm{dx}&\\[5pt]
&=& \left[0,0015\cdot x^4 - \frac{1}{30}\cdot x^3 +4,5\cdot x\right]_0^{11,1}&\\[5pt]
&=& 0,0015\cdot 11,1^4 - \frac{1}{30}\cdot 11,1^3 +4,5\cdot 11,1 - (0,0015\cdot 0^4 - \frac{1}{30}\cdot 0^3 +4,5\cdot 0)&\\[5pt]
&=& 22,7711 - 45,5877 +49,95 - 0&\\[5pt]
&=& 27,13&
\end{array}\)](https://mathjax.schullv.de/c85ec59c03a993360df01d0a619047e77c41cb62c8c85509c7f8bba146cbe269?color=5a5a5a) Der gesuchte Flächeninhalt beträgt
Der gesuchte Flächeninhalt beträgt  .
.
 Seitenfläche zerlegen
Jede Seitenfläche soll in zwei Teilflächen zerlegt werden, die mit verschiedenen Materialien verkleidet werden.
Seitenfläche zerlegen
Jede Seitenfläche soll in zwei Teilflächen zerlegt werden, die mit verschiedenen Materialien verkleidet werden.
Durch den Term kann für
kann für  der Flächeninhalt einer Teilfläche berechnet werden.
Du sollst nun die diesem Term zugrundeliegende Zerlegung erläutern, dazu sollst du auch mithilfe einer Skizze in der Abbildung 1 der Anlage für einen geeigneten Wert
der Flächeninhalt einer Teilfläche berechnet werden.
Du sollst nun die diesem Term zugrundeliegende Zerlegung erläutern, dazu sollst du auch mithilfe einer Skizze in der Abbildung 1 der Anlage für einen geeigneten Wert  arbeiten.
arbeiten.
Die Fläche wird durch eine horizontale Strecke, die durch den Punkt verläuft, zerlegt. Die untere Teilfläche besteht dann aus einem Rechteck mit den Kantenlängen
verläuft, zerlegt. Die untere Teilfläche besteht dann aus einem Rechteck mit den Kantenlängen  und
und  und der Fläche unterhalb der Rutsche, also der Fläche unter
und der Fläche unterhalb der Rutsche, also der Fläche unter  für
für  . Die Skizze sieht beispielsweise folgendermaßen aus:
. Die Skizze sieht beispielsweise folgendermaßen aus:
 Eine andere Zerlegung der Seitenfläche ergibt sich aus der Gleichung
Eine andere Zerlegung der Seitenfläche ergibt sich aus der Gleichung
 .
Du sollst die dieser Gleichung zugrundeliegende Zerlegung auch mithilfe einer Skizze in der Abbildung 2 erläutern. Mit dieser Gleichung wird eine Stelle
.
Du sollst die dieser Gleichung zugrundeliegende Zerlegung auch mithilfe einer Skizze in der Abbildung 2 erläutern. Mit dieser Gleichung wird eine Stelle  bestimmt, sodass eine Ursprungsgerade durch den Punkt
bestimmt, sodass eine Ursprungsgerade durch den Punkt  existiert, die die Seitenfläche in zwei gleich große Teile teilt. Eine solche Gerade sollst du dann noch in Abbildung 2 einzeichnen:
existiert, die die Seitenfläche in zwei gleich große Teile teilt. Eine solche Gerade sollst du dann noch in Abbildung 2 einzeichnen:


Du kannst das Integral jedoch auch von Hand berechnen:
Durch den Term
Die Fläche wird durch eine horizontale Strecke, die durch den Punkt


Für den Verlauf einer Rutsche werden für  die Funktion
die Funktion  mit
mit  und für
und für  die Funktion
die Funktion  mit
mit  verwendet;
verwendet;  in Metern,
in Metern,  und
und  Höhe über dem Boden in Metern. Der waagerechte Boden ist durch die
Höhe über dem Boden in Metern. Der waagerechte Boden ist durch die  -Achse gegeben.
-Achse gegeben.
a)  Höhe der Rutsche am Startpunkt
Du sollst die Höhe der Rutsche am Startpunkt bestimmen. Dafür berechnest du
Höhe der Rutsche am Startpunkt
Du sollst die Höhe der Rutsche am Startpunkt bestimmen. Dafür berechnest du  , da die Funktion
, da die Funktion  den Startbereich der Rutsche modelliert und der Startpunkt bei
den Startbereich der Rutsche modelliert und der Startpunkt bei  liegt.
liegt.
 Die Höhe im Startpunkt der Rutsche beträgt
Die Höhe im Startpunkt der Rutsche beträgt  .
.
 Durchschnittliche Steigung im Startbereich
Um die durchschnittliche Steigung im Startbereich zu berechnen, benötigst du die mittlere Änderungsrate:
Durchschnittliche Steigung im Startbereich
Um die durchschnittliche Steigung im Startbereich zu berechnen, benötigst du die mittlere Änderungsrate:
 Der Startbereich beginnt bei
Der Startbereich beginnt bei  und endet bei
und endet bei  . Berechne also mit diesen Werten und der Formel für die mittlere Änderungsrate die gesuchte durchschnittliche Steigung:
. Berechne also mit diesen Werten und der Formel für die mittlere Änderungsrate die gesuchte durchschnittliche Steigung:
![\(\begin{array}{rll}
\Delta m&=&\dfrac{f(0) - f(-6)}{0 - (-6)} \\[5pt]
&=&\dfrac{4,5 - 7,92}{0 +6} \\[5pt]
&=&\dfrac{-3,42}{6} \\[5pt]
&=& -0,57 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/b3fa078f3869c2a205013abbb97c8d45393689a7450d951f125406f2b3e18ab3?color=5a5a5a) Die durchschnittliche Steigung im Startbereich beträgt somit
Die durchschnittliche Steigung im Startbereich beträgt somit 
 Betragsmäßig größte Steigung im Startbereich
Außerdem sollst du die betragsmäßig größte Steigung im Startbereich berechnen. Die Ableitung der Funktion
Betragsmäßig größte Steigung im Startbereich
Außerdem sollst du die betragsmäßig größte Steigung im Startbereich berechnen. Die Ableitung der Funktion  beschreibt die Steigung im Startbereich. Da
beschreibt die Steigung im Startbereich. Da  auf dem Bereich
auf dem Bereich  monoton fällt (Steigung negativ), ist die betragsmäßig größte Steigung das Minimum der Ableitung von
monoton fällt (Steigung negativ), ist die betragsmäßig größte Steigung das Minimum der Ableitung von  . Berechne also zunächst die ersten 3 Ableitungen von
. Berechne also zunächst die ersten 3 Ableitungen von  :
:
![\(\begin{array}{rll}
f(x)&=&0,03\cdot x^3 + 0,275 \cdot x^2 + 4,5\\[5pt]
f‘(x)&=&0,09\cdot x^2 + 0,55 \cdot x\\[5pt]
f‘‘(x)&=&0,18\cdot x + 0,55\\[5pt]
f‘‘‘(x)&=&0,18\\[5pt]
\end{array}\)](https://mathjax.schullv.de/9d4538b7f93a38a142ddf258a178b4ecc9905d5c136499a832cb2d6432cee44d?color=5a5a5a) Um das Minimum der 1. Ableitung zu bestimmen, musst du die Nullstelle der 2. Ableitung berechnen:
Um das Minimum der 1. Ableitung zu bestimmen, musst du die Nullstelle der 2. Ableitung berechnen:
![\(\begin{array}{rll}
f‘‘(x)&=&0\\[5pt]
0&=&0,18\cdot x + 0,55&\scriptsize \mid\; -0,55\\[5pt]
-0,55&=&0,18 \cdot x&\scriptsize \mid\; :0,18\\[5pt]
x &=& -3,056
\end{array}\)](https://mathjax.schullv.de/2e33cee57d99dce9684f1465f7ed4f3e958697a7be1050b120147bf5ad51213f?color=5a5a5a) Die Nullstelle der 2. Ableitung ist gegeben durch
Die Nullstelle der 2. Ableitung ist gegeben durch  . Es handelt sich tatsächlich um ein Minimum, da die 3. Ableitung an der Stelle
. Es handelt sich tatsächlich um ein Minimum, da die 3. Ableitung an der Stelle  positiv ist:
positiv ist:
 Um die betragsmäßig größte Steigung zu berechnen, setze nun
Um die betragsmäßig größte Steigung zu berechnen, setze nun  in die 1. Ableitung ein:
in die 1. Ableitung ein:
 Die betragsmäßig größte Steigung ist somit gegeben durch
Die betragsmäßig größte Steigung ist somit gegeben durch  .
.
 Übergang zwischen
Übergang zwischen  und
und  Du sollst nachweisen, dass der Übergang zwischen der Modellierung mit
Du sollst nachweisen, dass der Übergang zwischen der Modellierung mit  und
und  sprung- und knickfrei ist. Dafür müssen zwei Bedingungen erfüllt sein:
sprung- und knickfrei ist. Dafür müssen zwei Bedingungen erfüllt sein:
 hast du bereits berechnet. Berechne also noch die Ableitung von
hast du bereits berechnet. Berechne also noch die Ableitung von  .
.
 Überprüfe nun die beiden Bedingungen.
Überprüfe nun die beiden Bedingungen.
 Da beide Bedingungen erfüllt sind, verläuft der Übergang zwischen der Modellierung von
Da beide Bedingungen erfüllt sind, verläuft der Übergang zwischen der Modellierung von  und
und  sprung- und knickfrei.
sprung- und knickfrei.
 Knickfreier Übergang in Auslaufbereich der Rutsche
Du sollst die Stelle berechnen, an der die Rutsche enden muss, damit sie knickfrei in einen waagerechten Auslaufbereich übergeht. Das heißt die Steigung muss übereinstimmen. Eine waagrechte Strecke hat eine Steigung von
Knickfreier Übergang in Auslaufbereich der Rutsche
Du sollst die Stelle berechnen, an der die Rutsche enden muss, damit sie knickfrei in einen waagerechten Auslaufbereich übergeht. Das heißt die Steigung muss übereinstimmen. Eine waagrechte Strecke hat eine Steigung von  , somit muss auch die Funktion
, somit muss auch die Funktion  eine Steigung von
eine Steigung von  haben. Berechne also
haben. Berechne also  , um die gesuchte Übergangsstelle zu berechnen:
, um die gesuchte Übergangsstelle zu berechnen:
![\(\begin{array}{rll}
0&=&g‘(x)& \\
0&=&0,018\cdot x^2 - 0,2\cdot x&\scriptsize (x \text{ ausklammern}) \\[5pt]
0&=&(0,018\cdot x - 0,2)\cdot x&\scriptsize (x_1 = 0) \\[5pt]
0&=&0,018\cdot x - 0,2&\scriptsize \mid\; +0,2\\[5pt]
0,2&=&0,018\cdot x&\scriptsize \mid\; :0,018\\[5pt]
x_2&=&11,11&
\end{array}\)](https://mathjax.schullv.de/a438fea3ab3fc001daff4d9761eb51dbf2534d83837da3c54ea9cd2eefe2303d?color=5a5a5a) Die Stelle, an der die Rutsche knickfrei in einen waagrechten Auslaufbereich übergeht, ist gegeben durch
Die Stelle, an der die Rutsche knickfrei in einen waagrechten Auslaufbereich übergeht, ist gegeben durch  .
.
(Vermeidung des Sprungs)
(Vermeidung des Knicks)
b)  Funktion der Flugbahn berechnen
Rutscht der Badegast schnell genug, so berührt er nach dem Startbereich die Rutsche nicht mehr und fliegt ein Stück durch die Luft. Seine Flugbahn lässt sich vereinfacht beschreiben durch eine Funktion
Funktion der Flugbahn berechnen
Rutscht der Badegast schnell genug, so berührt er nach dem Startbereich die Rutsche nicht mehr und fliegt ein Stück durch die Luft. Seine Flugbahn lässt sich vereinfacht beschreiben durch eine Funktion  mit
mit  ;
; 
 ;
; 
 in Metern,
in Metern,  Höhe über dem Boden in Metern.
Höhe über dem Boden in Metern.
Du sollst so berechnen, dass der Badegast im Punkt
so berechnen, dass der Badegast im Punkt  wieder auf die Rutsche trifft. Der Badegast trifft also auf die Funktion
wieder auf die Rutsche trifft. Der Badegast trifft also auf die Funktion  . Der Graph der Funktion
. Der Graph der Funktion  und der Graph der Funktion
und der Graph der Funktion  müssen dann an der Stelle
müssen dann an der Stelle  , an der der Badegast wieder auf die Rutsche trifft, die gleiche Höhe haben. Es gilt also:
, an der der Badegast wieder auf die Rutsche trifft, die gleiche Höhe haben. Es gilt also:
 Der Punkt
Der Punkt  hat dann folgende Form
hat dann folgende Form  .
.
Durch Einsetzen des Punktes in
in  kannst du den Parameter
kannst du den Parameter  berechnen:
berechnen:
![\(\begin{array}{rll}
p(5)&=&a\cdot 5^2 + 4,5&\\[5pt]
2,75&=&a\cdot 25 + 4,5&\scriptsize \mid\; -4,5\\[5pt]
-1,75&=&a\cdot 25 &\scriptsize \mid\; :25\\[5pt]
a&=&-0,07 &\scriptsize \mid\; :25\\[5pt]
\end{array}\)](https://mathjax.schullv.de/b1a30250cfa73bba6d959abb39c172a8dae58ce9562b851db73b304ba4fd54a6?color=5a5a5a) Die Flugbahn des Badegasts wird modelliert durch
Die Flugbahn des Badegasts wird modelliert durch  .
.
 Vergleich der Steigungen von Flugbahn und Rutsche im Auftreffpunkt
Du sollst untersuchen, ob sich die Steigung der Flugbahn des Badegasts am Auftreffpunkt
Vergleich der Steigungen von Flugbahn und Rutsche im Auftreffpunkt
Du sollst untersuchen, ob sich die Steigung der Flugbahn des Badegasts am Auftreffpunkt  betragsmäßig um mehr als 0,1 von der Steigung der Rutsche an dieser Stelle unterscheidet. Berechne dafür zunächst die Ableitung von
betragsmäßig um mehr als 0,1 von der Steigung der Rutsche an dieser Stelle unterscheidet. Berechne dafür zunächst die Ableitung von  , die Ableitung von
, die Ableitung von  hast du bereits etwas früher in dieser Aufgabe berechnet.
hast du bereits etwas früher in dieser Aufgabe berechnet.
 Berechne nun die Steigung an der Stelle
Berechne nun die Steigung an der Stelle  für beide Funktionen:
für beide Funktionen:
 Berechne nun die Steigungsdifferenz:
Berechne nun die Steigungsdifferenz:
 Der Steigungsunterschied ist größer als 0,1.
Der Steigungsunterschied ist größer als 0,1.
Du sollst
Durch Einsetzen des Punktes
c)  Flächeninhalt der Seitenfläche berechnen
Die Seitenflächen der Rutsche sollen für
Flächeninhalt der Seitenfläche berechnen
Die Seitenflächen der Rutsche sollen für  bis zum Boden verkleidet werden. Du sollst nun den Flächeninhalt
bis zum Boden verkleidet werden. Du sollst nun den Flächeninhalt  einer der zu verkleidenden Seitenflächen berechnen. Es ist also der Wert des folgenden Integrals gesucht:
einer der zu verkleidenden Seitenflächen berechnen. Es ist also der Wert des folgenden Integrals gesucht:
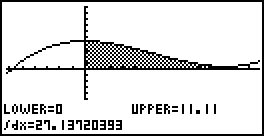
 Das Integral kannst du mithilfe deines Graphiktaschenrechners lösen. Zeichne dazu den Graphen der Funktion
Das Integral kannst du mithilfe deines Graphiktaschenrechners lösen. Zeichne dazu den Graphen der Funktion  und nutze die Integralfunktion aus dem G-Solv-Menü.
und nutze die Integralfunktion aus dem G-Solv-Menü.
 Alternativ
Alternativ
Du kannst das Integral jedoch auch von Hand berechnen:![\(\begin{array}{rll}
\displaystyle\int_{0}^{11,1} g(x) \mathrm{dx}&=&\displaystyle\int_{0}^{11,1} (0,006\cdot x^3 - 0,1\cdot x^2 +4,5) \mathrm{dx}&\\[5pt]
&=& \left[0,0015\cdot x^4 - \frac{1}{30}\cdot x^3 +4,5\cdot x\right]_0^{11,1}&\\[5pt]
&=& 0,0015\cdot 11,1^4 - \frac{1}{30}\cdot 11,1^3 +4,5\cdot 11,1 - (0,0015\cdot 0^4 - \frac{1}{30}\cdot 0^3 +4,5\cdot 0)&\\[5pt]
&=& 22,7711 - 45,5877 +49,95 - 0&\\[5pt]
&=& 27,13&
\end{array}\)](https://mathjax.schullv.de/c85ec59c03a993360df01d0a619047e77c41cb62c8c85509c7f8bba146cbe269?color=5a5a5a) Der gesuchte Flächeninhalt beträgt
Der gesuchte Flächeninhalt beträgt  .
.
 Seitenfläche zerlegen
Jede Seitenfläche soll in zwei Teilflächen zerlegt werden, die mit verschiedenen Materialien verkleidet werden.
Seitenfläche zerlegen
Jede Seitenfläche soll in zwei Teilflächen zerlegt werden, die mit verschiedenen Materialien verkleidet werden.
Durch den Term kann für
kann für  der Flächeninhalt einer Teilfläche berechnet werden.
Du sollst nun die diesem Term zugrundeliegende Zerlegung erläutern, dazu sollst du auch mithilfe einer Skizze in der Abbildung 1 der Anlage für einen geeigneten Wert
der Flächeninhalt einer Teilfläche berechnet werden.
Du sollst nun die diesem Term zugrundeliegende Zerlegung erläutern, dazu sollst du auch mithilfe einer Skizze in der Abbildung 1 der Anlage für einen geeigneten Wert  arbeiten.
arbeiten.
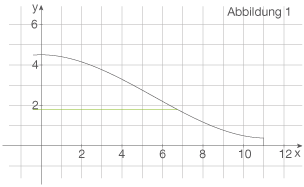
Die Fläche wird durch eine horizontale Strecke, die durch den Punkt verläuft, zerlegt. Die untere Teilfläche besteht dann aus einem Rechteck mit den Kantenlängen
verläuft, zerlegt. Die untere Teilfläche besteht dann aus einem Rechteck mit den Kantenlängen  und
und  und der Fläche unterhalb der Rutsche, also der Fläche unter
und der Fläche unterhalb der Rutsche, also der Fläche unter  für
für  . Die Skizze sieht beispielsweise folgendermaßen aus:
. Die Skizze sieht beispielsweise folgendermaßen aus:
 Eine andere Zerlegung der Seitenfläche ergibt sich aus der Gleichung
Eine andere Zerlegung der Seitenfläche ergibt sich aus der Gleichung
 .
Du sollst die dieser Gleichung zugrundeliegende Zerlegung auch mithilfe einer Skizze in der Abbildung 2 erläutern. Mit dieser Gleichung wird eine Stelle
.
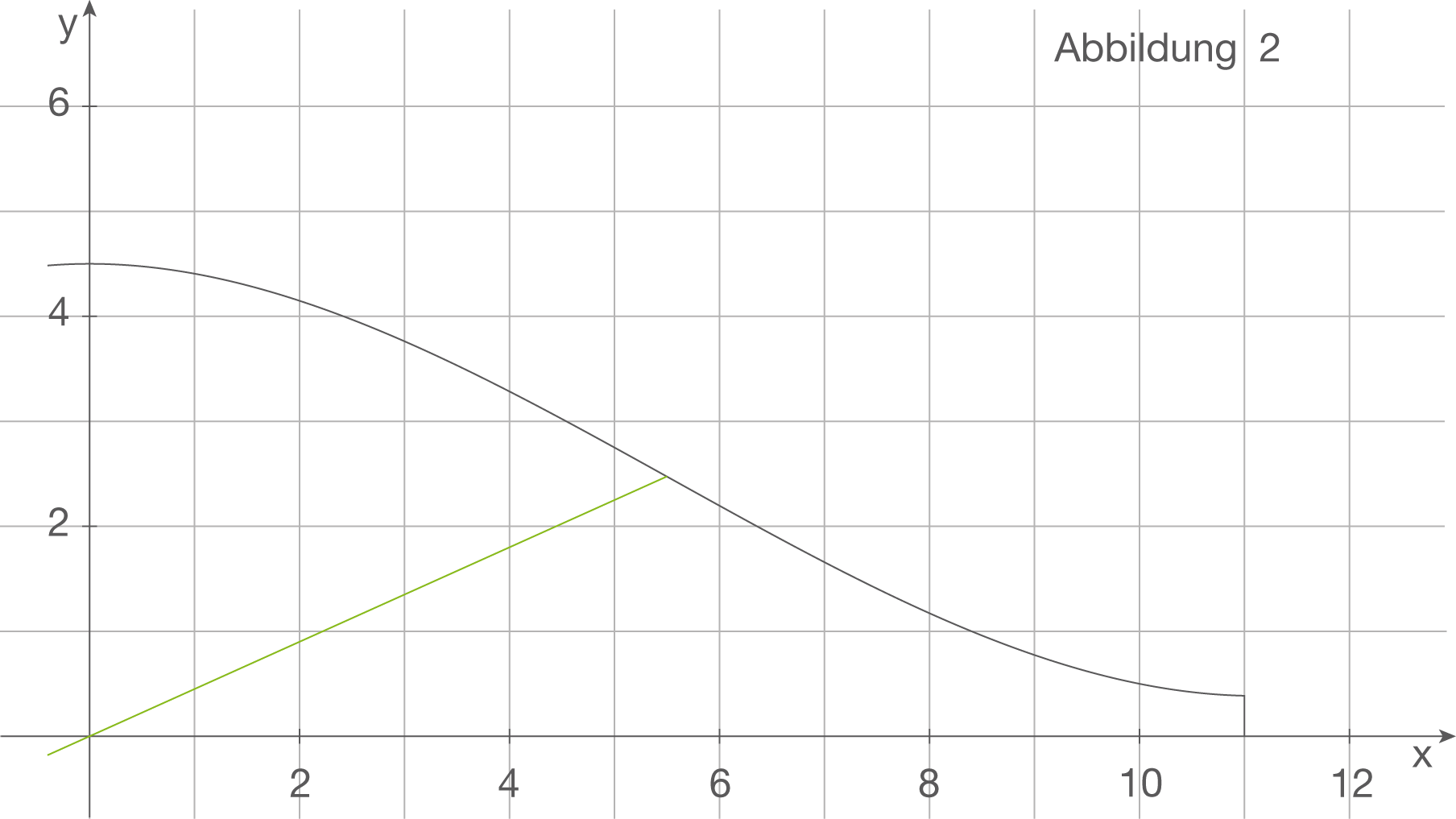
Du sollst die dieser Gleichung zugrundeliegende Zerlegung auch mithilfe einer Skizze in der Abbildung 2 erläutern. Mit dieser Gleichung wird eine Stelle  bestimmt, sodass eine Ursprungsgerade durch den Punkt
bestimmt, sodass eine Ursprungsgerade durch den Punkt  existiert, die die Seitenfläche in zwei gleich große Teile teilt. Eine solche Gerade sollst du dann noch in Abbildung 2 einzeichnen:
existiert, die die Seitenfläche in zwei gleich große Teile teilt. Eine solche Gerade sollst du dann noch in Abbildung 2 einzeichnen:
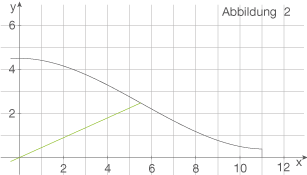

Du kannst das Integral jedoch auch von Hand berechnen:
Durch den Term
Die Fläche wird durch eine horizontale Strecke, die durch den Punkt

