Aufgabe 3B

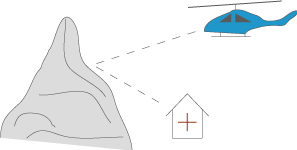
Illustration eines Berges mit drei blauen Hubschraubern, die zu einem roten Kreuz auf einem Haus fliegen.

Eine Gruppe Bergsteiger gerät am Berg in Not und funkt nach Hilfe.
In einem passenden Koordinatensystem befindet sich die Bergwacht im Ursprung $O(0\mid0\mid0)$ .
Ein Hubschrauber befindet sich im Punkt $H(-4\mid6\mid1)$ . Alle Koordinaten haben die Einheit km.

a) Der Notruf der Bergsteiger wird von der Bergwacht aus der Richtung $\vec{u}=\begin{pmatrix}1\\-3\\2\end{pmatrix}$ aufgenommen.

Der Hubschrauber nimmt den Notruf aus der Richtung $\vec{v}=\begin{pmatrix}2\\-4\\1\end{pmatrix}$ auf.
Berechnen Sie die Koordinaten des Punktes $N$ , in dem sich die Bergsteigergruppe aufhält.

(Zur Kontrolle: $N(2\mid-6\mid4)$ )

Der Hubschrauber fliegt sofort zum Aufenthaltsort der Bergsteigergruppe. Vereinfachend wird angenommen, dass seine Geschwindigkeit konstant $250\frac{\text{km}}{\text{h}}$ beträgt.

Berechnen Sie seine Flugzeit bis zum Eintreffen im Punkt $N$ in Minuten.

(9P)

b) Der Hubschrauber nimmt die Bergsteigergruppe auf und fliegt vom Aufenthaltsort in Punkt $N$ zur Bergwacht. Dabei fliegt er vom Punkt $N$ aus zunächst zum Punkt $P(1,5\mid-6\mid3)$ und von dort aus weiter mit dem Kurs $\vec{k}=\begin{pmatrix}-0,5\\2\\-1\end{pmatrix}$ .
Zeigen Sie, dass der Hubschrauber die Bergwacht erreicht.

Berechnen Sie den Neigungswinkel der Flugbahn, auf der der Hubschrauber die Bergwacht anfliegt.

(Hinweis: Der Neigungswinkel ist der Winkel gegen die Horizontale.)

(8P)

(17P)

In einem passenden Koordinatensystem befindet sich die Bergwacht im Ursprung $O(0\mid0\mid0)$ . Ein Hubschrauber befindet sich im Punkt $H(-4\mid6\mid1)$ . Alle Koordinaten haben die Einheit km.

a) $\blacktriangleright$ Koordinaten des Punktes $\boldsymbol{N}$ , in dem sich die Bergsteigergruppe befindet

Der Notruf der Bergsteiger wird von der Bergwacht aus der Richtung $\vec{u}=\begin{pmatrix}1\\-3\\2\end{pmatrix}$ aufgenommen. Der Hubschrauber nimmt den Notruf aus der Richtung $\vec{v}=\begin{pmatrix}2\\-4\\1\end{pmatrix}$ auf.
Du sollst die Koordinaten des Punktes $N$ , in dem sich die Bergsteigergruppe aufhält, berechnen. Lege dafür eine Gerade durch den Ort der Bergwacht und eine zweite Gerade durch den Aufenthaltsort des Hubschraubers. Die Richtungsvektoren der Geraden sind dir in der Aufgabenstellung gegeben:

Bergwacht: $\vec{x} = O + s\cdot \vec{u} = \begin{pmatrix}0\\0\\0\end{pmatrix} + s\cdot \begin{pmatrix}1\\-3\\2\end{pmatrix} = s\cdot \begin{pmatrix}1\\-3\\2\end{pmatrix}$

Hubschrauber: $\vec{x} = H + t\cdot \vec{v} = \begin{pmatrix}-4\\6\\1\end{pmatrix} + t\cdot \begin{pmatrix}2\\-4\\1\end{pmatrix}$

Um den Aufenthaltsort der Bergsteigergruppe zu bestimmen, musst du den Schnittpunkt der beiden Geraden berechnen.

$\begin{array}{rll} s\cdot \begin{pmatrix}1\\-3\\2\end{pmatrix}&=&\begin{pmatrix}-4\\6\\1\end{pmatrix} + t\cdot \begin{pmatrix}2\\-4\\1\end{pmatrix}&\scriptsize \mid - t\cdot \begin{pmatrix}2\\-4\\1\end{pmatrix}\\ s\cdot \begin{pmatrix}1\\-3\\2\end{pmatrix} - t\cdot \begin{pmatrix}2\\-4\\1\end{pmatrix}&=&\begin{pmatrix}-4\\6\\1\end{pmatrix} & \end{array}$

Daraus ergibt sich folgendes lineares Geichungssystem:

$\begin{array}{l@{\qquad}*{3}{rc}r@{\qquad}l} (1)&-4&=&s&-&2t&&\\ (2)&6&=&-3s&+&4t&&&\\ (3)&1&=&2s&-&t&&&\mid \scriptsize{Rechne: }2\cdot(1)+(2)\\ \end{array}$

$\begin{array}{l@{\qquad}*{3}{rc}r@{\qquad}l} (1)&-4&=&s&-&2t&&\\ (2)&-2&=&-s&&&&&\\ (3)&1&=&2s&-&t&&& \end{array}$

Aus Gleichung (2) folgt $s = 2$ . Durch Einsetzen in (3) ergibt sich:

$\begin{array}{rll} 1&=&2 \cdot 2 - t&\\ 1&=&4 - t&\scriptsize \mid -4 \\ -3&=&- t&\scriptsize \mid :(-1)\\ t&=&3& \end{array}$

Somit gilt $t = 3$ . Das Einsetzen von $s$ oder $t$ in die jeweilige Geradengleichung liefert dann den Schnittpunkt der Geraden. Setze also $s$ in die Geradengleichung der Bergwacht ein:

$N = 2\cdot \begin{pmatrix}1\\-3\\2\end{pmatrix} = \begin{pmatrix}2\\-6\\4\end{pmatrix}$

Der Punkt $N(2\mid -6\mid 4)$ gibt den Aufenthaltsort der Bergsteigergruppe an.

$\blacktriangleright$ Flugzeit berechnen

Du sollst seine Flugzeit bis zum Eintreffen im Punkt $N$ in Minuten berechnen. Vereinfachend wird angenommen, dass seine Geschwindigkeit konstant $250\frac{\text{km}}{\text{h}}$ beträgt.

Berechne dafür zuerst du Länge der Strecke $\overline{HN}$ :

$\mid \overline{HN} \mid = \left|\begin{pmatrix}6\\-12\\3\end{pmatrix}\right| = \sqrt{36 + 144 + 9} = \sqrt{189} = 13,75$ km

Die Entfernung vom Hubschrauber zur Bergsteigergruppe beträgt 13,75 km.
Die Zeit bis der Hubschrauber eintrifft kannst du mithilfe der angegebenen Geschwindigkeit berechnen:

$\dfrac{13,75 \text{km}}{250 \frac{\text{km}}{\text{h}}} = 0,055 \text{h}$

Rechne die Stundenangabe jetzt noch in Minuten um, indem du das Ergebnis mit 60 multiplizierst:

$t = 0,055 \cdot 60 = 3,3$ min

Der Hubschrauber braucht also $3,3$ Minuten um zum Ort der Bergsteiger zu gelangen.

b) $\blacktriangleright$ Beweise die Aussage

Der Hubschrauber nimmt die Bergsteigergruppe auf und fliegt vom Aufenthaltsort in Punkt $N$ zur Bergwacht. Dabei fliegt er vom Punkt $N$ aus zunächst zum Punkt $P(1,5\mid-6\mid3)$ und von dort aus weiter mit dem Kurs

$\vec{k}=\begin{pmatrix}-0,5\\2\\-1\end{pmatrix}$ .

Du sollst zeigen, dass der Hubschrauber die Bergwacht erreicht. Stelle dafür eine Gerade durch den Punkt $P$ mit Richtungsvektor $\vec{k}$ auf:

$g: \vec{x} = \overline{OP} + r\cdot \vec{k} = \begin{pmatrix}1,5 \\ -6 \\ 3\end{pmatrix} + r\cdot \begin{pmatrix}-0,5\\2\\-1\end{pmatrix}$

Damit der Hubschrauber die Bergwacht erreicht, muss die Gerade der Flugbahn durch den Punkt $O$ verlaufen. Mache also eine Punktprobe mit $O$ :

$\begin{pmatrix}0\\0\\0\end{pmatrix}= \begin{pmatrix}1,5 \\ -6 \\ 3\end{pmatrix} + r\cdot \begin{pmatrix}-0,5\\2\\-1\end{pmatrix}$

Du erhältst folgende Gleichungen:

$\begin{array}{l@{\qquad}*{3}{rc}r@{\qquad}l} (1)&0&=&1,5&-&0,5r&&\\ (2)&0&=&-6&+&2r&&\\ (3)&0&=&3&-&r&& \end{array}$

Durch Umstellen der Gleichung (3) erhältst du $r=3$ . Du musst nun noch überprüfen ob dieses $r$ auch die anderen Gleichungen erfüllt:

$\begin{array}{l@{\qquad}*{3}{rc}r@{\qquad}l} (1)&0&=&1,5&-&0,5\cdot 3&&\\ (2)&0&=&-6&+&2\cdot 3&& \end{array}$

Da alle Gleichungen erfüllt sind, liegt $O$ auf der Geraden. Der Hubschrauber erreicht die Bergwacht.

$\blacktriangleright$ Neigungswinkel der Flugbahn berechnen

Berechnen Sie den Neigungswinkel $\alpha$ der Flugbahn $g$ , auf der der Hubschrauber die Bergwacht anfliegt. Der Neigungswinkel ist der Winkel gegen die Horizontale, also gegen die $x_1-x_2$ -Ebene. Den Winkel zwischen Vektor und Ebene berechnest du mit folgender Formel:

$\alpha = \arcsin\left(\dfrac{\mid \vec{u} \cdot \vec{n}\mid}{\mid \vec{u}\mid \cdot \mid \vec{n}\mid}\right)$

wobei $\vec{n}$ der Normalenvektor der Ebene ist.
Ein Normalenvektor auf die $x_1-x_2$ -Ebene ist gegeben durch $\vec{n} = \begin{pmatrix}0\\0\\1\end{pmatrix}$ , der Vektor ist gegeben durch $\vec{u} = \begin{pmatrix}1,5\\-6\\3\end{pmatrix}$ . Jetzt kannst du den Winkel $\alpha$ berechnen:

$\mid \vec{u} \cdot \vec{n}\mid = \left|\begin{pmatrix}0\\0\\1\end{pmatrix}\cdot \begin{pmatrix}1,5\\-6\\3\end{pmatrix}\right| = 3$
$\mid \vec{u} \mid = \left|\begin{pmatrix}1,5\\-6\\3\end{pmatrix}\right| = \sqrt{1,5^2 + (-6)^2 + 3^2} = \sqrt{2,25 + 36 + 9} = \sqrt{47,25}$
$\mid \vec{n} \mid = \left|\begin{pmatrix}0\\0\\1\end{pmatrix}\right| = \sqrt{0^2 + 0^2 + 1^2} = 1$

$\alpha = \arcsin \left(\dfrac{3}{\sqrt{47,25} \cdot 1}\right) = \arcsin (0.4364) = 25,9\;^{\circ}$

Der Neigungswinkel beträgt $25,9 ^{\circ}$ .