Analysis

Gegeben sind die Punkte $T_1(-2\mid2),$ $T_2(2\mid2)$ und $H(0\mid4).$

1.1

Bestimme einen Funktionsterm der Polynomfunktion vom Grad $4,$ deren Schaubild $K$ die folgenden drei Eigenschaften hat:

$K$ ist symmetrisch zur $y$ -Achse.
$K$ schneidet die $y$ -Achse im Punkt $H.$
$K$ hat einen Extrempunkt in $T_1.$

1.2

Gegeben ist die Funktion $f$ mit

$f(x)=\dfrac{1}{8}x^4-x^2+4;$ $-3\leq x\leq 3.$

Das Schaubild von $f$ ist $K_f$ (siehe Abbildung).

bw abi berufliches gymnasium technisch teil 2 aufgabe 1 abbildung 1 funktion f

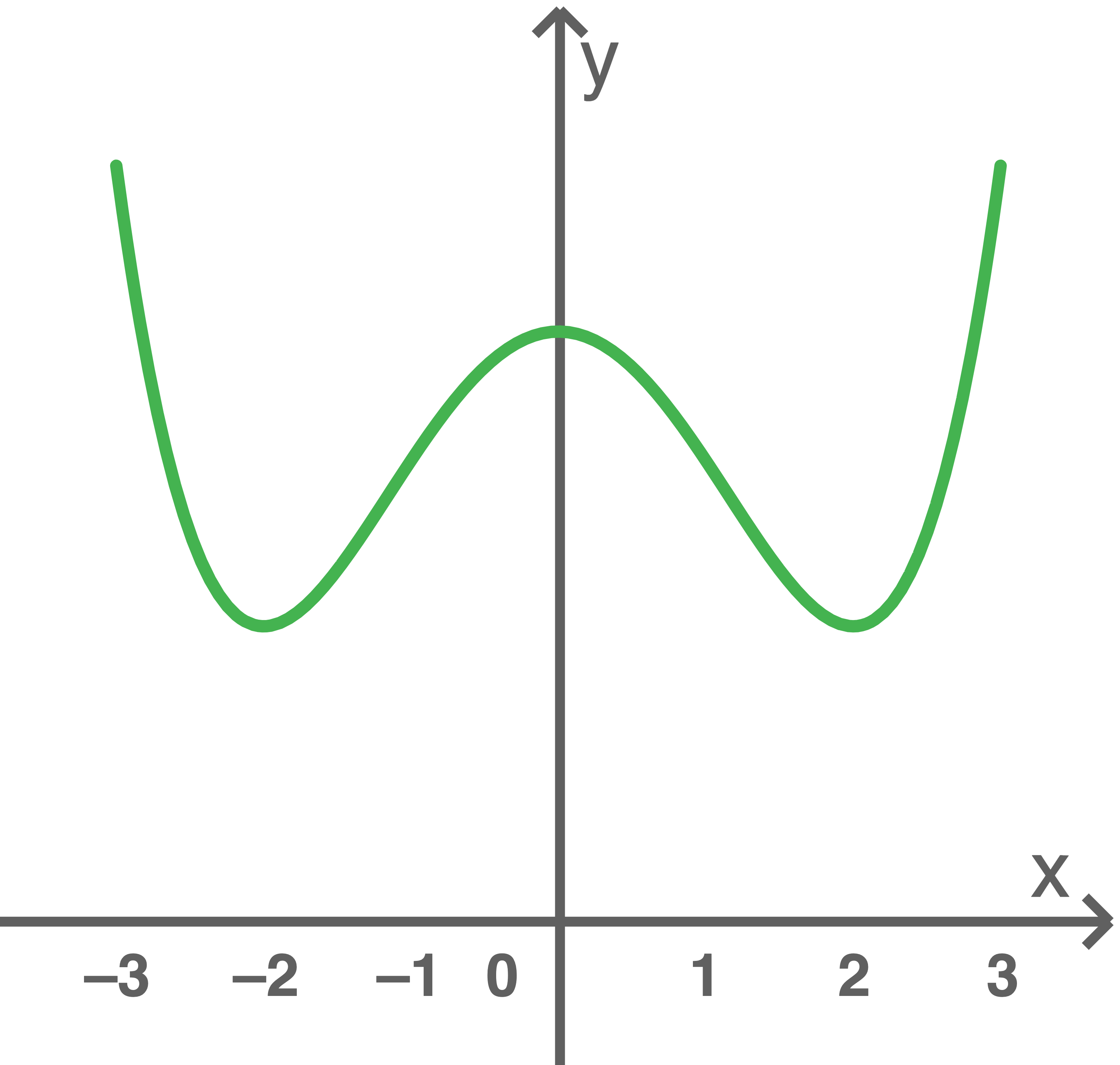
1.2.1

Die Funktionsgleichung von $f$ lässt sich in der Form

$f(x)=a(x+b)^2(x+c)^2+2$

darstellen. Gib passende Werte für $a,$ $b$ und $c$ an.

1.2.2

Eine nach unten geöffnete Parabel, die $H$ als Scheitelpunkt hat, schneidet $K_f$ in einem Punkt $S(x_0\mid f(x_0))$ mit $x_0\gt0.$ Begründe, dass $x_0\lt2\sqrt{2}$ gilt.

1.2.3

Ermittle den größten Wert der ersten Ableitung von $f$ für $-3\leq x\leq3.$

1.3

Das Schaubild der Funktion $g$ mit $g(x)=\cos(u\cdot x)+v;$ $-3\leq x\leq 3,$ hat nur die drei Extrempunkte $T_1,$ $H$ und $T_2.$

1.3.1

Bestimme die Werte von $u$ und $v.$

1.3.2

Skizziere das Schaubild der Stammfunktion $G$ von $g$ mit $G(-3)=0.$
Begründe, dass die folgenden beiden Aussagen wahr sind:

(1)

Jede Stammfunktion von $g$ besitzt eine Umkehrfunktion.

(2)

Der Definitionsbereich einer solchen Umkehrfunktion ist ein Intervall der Länge $\displaystyle\int_{-3}^{3}g(x)\;\mathrm dx.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Da die Polynomfunktion von $K$ den Grad 4 hat und $K$ symmetrisch zur $y$ -Achse sein soll, hat der zugehörige Funktionsterm folgende Form:

$f(x) = a\cdot x^4 + b\cdot x^2 + c$

Da $K$ die $y$ -Achse im Punkt $H(0\mid 4)$ schneidet, folgt der $y$ -Achsenabschnitt $c = 4.$

Aus den Koordinaten von $T_1$ ergibt sich folgende Gleichung:

Rechenweg anzeigen

$\text{(I)}\quad 8a + 2b + 2=1$

Da $T_1$ ein Extrempunkt von $K$ sein soll, muss das notwendige Kriterium für Extrempunkte erfüllt sein. Es gilt also $\(f$

Für die erste Ableitung gilt $\(f$

$\(\begin{array}[t]{rll} f$

Die Gleichung kann nach $b$ umgestellt werden:

$\begin{array}[t]{rll} -32a -4b &=& 0 &\quad \scriptsize \mid\; :(-4) \\[5pt] 8a + b &=& 0 &\quad \scriptsize \mid\; -8a \\[5pt] b &=& -8a \end{array}$

Einsetzen in $\text{(I)}:$

Rechenweg anzeigen

$a= \frac{1}{8}$

Für $b$ ergibt sich: $b= -8\cdot \frac{1}{8} = -1.$

Das Schaubild $K$ von $f$ mit folgendem Funktionsterm erfüllt alle drei Eigenschaften:

$f(x)= \frac{1}{8}\cdot x^4 -x^2 +4$

1.2.1

Durch quadratische Ergänzung und Anwenden der 2. und 3. binomischen Formeln lässt sich der Funktionsterm wie folgt umschreiben:

Rechenweg anzeigen

$f(x)$ $=\frac{1}{8}\cdot (x +2)^2\cdot (x-2)^2 + 2$

Passende Werte sind also $a= \frac{1}{8},$ $b= 2$ und $c=-2.$

1.2.2

Da die Parabel nach unten geöffnet ist und $H$ ihr Scheitelpunkt ist, ist $H$ der höchste Punkt der Parabel.
Die $y$ -Koordinate des Schnittpunkts $S$ mit $K_f$ muss daher kleiner als die $y$ -Koordinate des Scheitelpunkts, also kleiner als $4$ sein. Also gilt:

Rechenweg anzeigen

$\begin{array}[t]{rll} f(x_0) &\lt & 4 \\[5pt] ...& &\\[5pt] \left| x_0\right| &\lt & 2 \sqrt{2} \\[5pt] \end{array}$

Also gilt insbesondere $x_0 \lt 2\sqrt{2}.$

1.2.3

Für die erste Ableitung von $f$ gilt:

$\(f$

1. Schritt: Notwendiges Kriterium für Extremstellen anwenden

Wegen des notwendigen Kriteriums für Extremstellen muss eine Extremstelle $x_E$ von $\(f$ die Gleichung $\(f$ erfüllen.

Es gilt $\(f$

Gleichsetzen ergibt:

$\(\begin{array}[t]{rll} f$

2. Schritt: Größten Wert der Ableitung bestimmen

Einsetzen der Intervallränder $-3$ und $3$ sowie der möglichen Extremstellen $-\frac{2}{\sqrt{3}}$ und $\frac{2}{\sqrt{3}}:$

Rechenweg anzeigen

$\(\begin{array}[t]{rll} f$

Der größte Wert der ersten Ableitung von $f$ für $-3\leq x\leq 3$ beträgt $7,5.$

1.3.1

Da die $y$ -Koordinate von $T_1$ und $T_2$ kleiner als die von $H$ ist, müssen $T_1$ und $T_2$ Tiefpunkte und $H$ ein Hochpunkt sein.
Bei $g$ handelt es sich um eine trigonometrische Funktion. Die Periodenlänge ergibt sich aus dem Abstand der beiden Tiefpunkte zu $p = 4.$
Mit der Periodenlänge lässt sich $u$ bestimmen:

$u = \frac{2\pi}{4} = \frac{1}{2}\pi$

Mit dem Wert von $v$ kann das Schaubild von $g$ soweit entlang der $y$ -Achse verschoben werden, dass die $y$ -Koordinaten der Hoch und Tiefpunkte stimmen.
Für $v=0$ wäre die $y$ -Koordinate des Hochpunkts $y=1.$ Das Schaubild muss also um drei Einheiten verschoben werden. Also ist $v=3.$

1.3.2

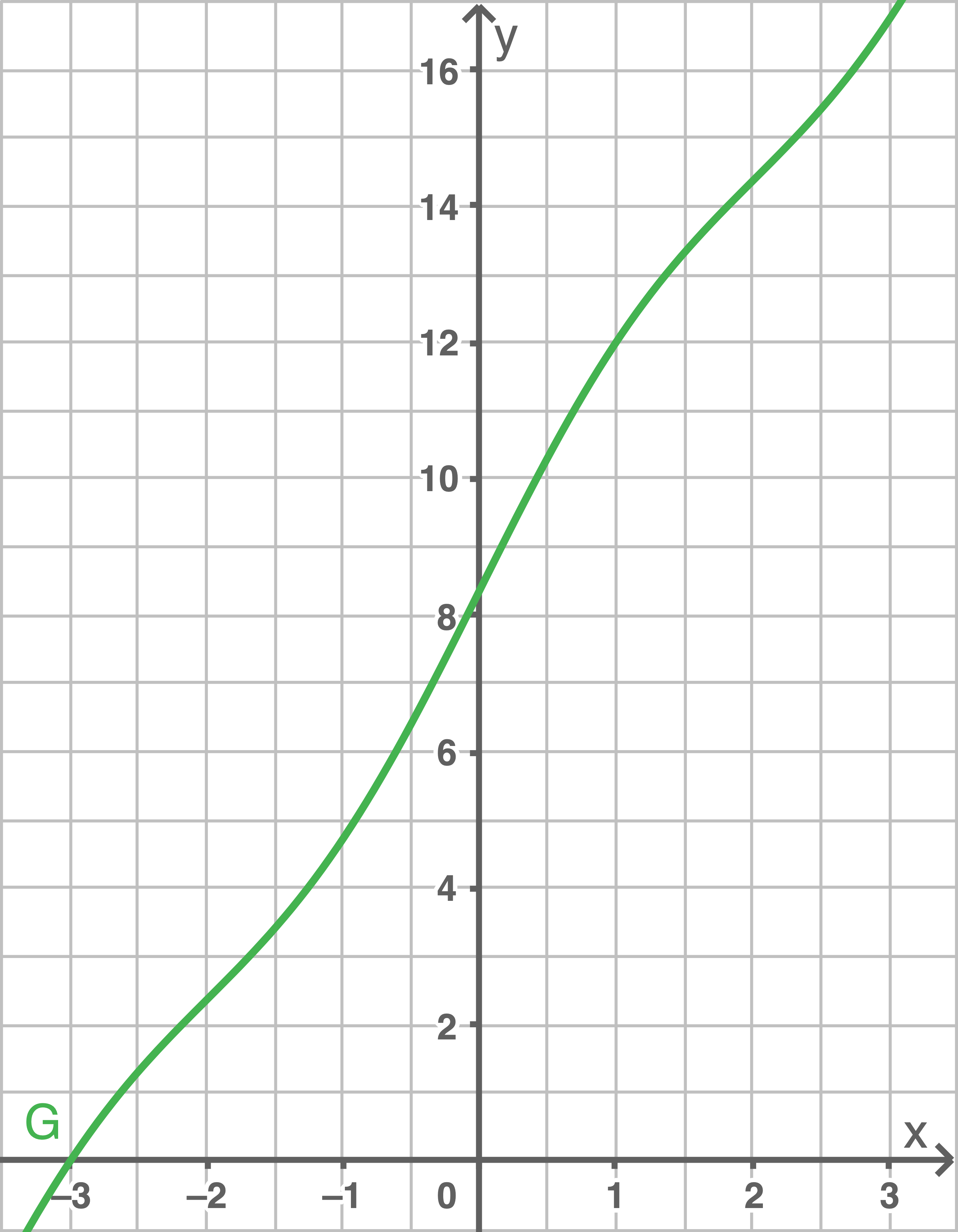
Stammfunktion - Baden-Württemberg Abi berufliches Gymnasium 2022 Mathe

Aussagen begründen

(1)

$G(x)$ gibt den Flächeninhalt zwischen dem Graphen von $g$ und der $x$ -Achse im Intervall von $-3$ bis $x$ an.
Da das Schaubild von $g$ vollständig oberhalb der $x$ -Achse verläuft nimmt dieser Flächeninhalt mit größerwerdendem $x$ zu. $G$ ist also streng monoton steigend.
Da die Schaubilder aller Stammfunktionen von $g$ durch Verschiebung entlang der $y$ -Achse aus dem von $G$ hervorgehen, sind daher alle Stammfunktionen von $g$ streng monoton steigend und besitzen somit jeweils eine Umkehrfunktion.

(2)

Der Definitionsbereich der Umkehrfunktion entspricht dem Wertebereich der eigentlichen Funktion.
Wie in (1) beschrieben, gibt $G(x)$ den Flächeninhalt zwischen dem Graphen von $g$ und der $x$ -Achse im Intervall von $-3$ bis $x$ an.
Der kleinste Funktionswert von $G$ ist also $G(-3)=0.$ Der größte Funktionswert wird wegen der Monotonie am Ende des Definitionsbereichs angenommen:

$G(3)= \displaystyle\int_{-3}^{3}g(x)\;\mathrm dx.$
Der Wertebereich von $G$ ist also $\left[0;\displaystyle\int_{-3}^{3}g(x)\;\mathrm dx\right]$ und die Länge des Wertebereichs dementsprechend $\displaystyle\int_{-3}^{3}g(x)\;\mathrm dx.$

Wie in (1) beschrieben, entsteht das Schaubild jeder Stammfunktion von $g$ durch Verschiebung des Schaubildes von $G.$ Die Wertebereiche weisen also dieselbe Länge auf, wodurch der Wertebereich jeder Stammfunktion von $g$ die Länge $\displaystyle\int_{-3}^{3}g(x)\;\mathrm dx$ hat und damit auch der Definitionsbereich der zugehörigen Umkehrfunktion.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?