Stochastik 1

Bei einem Festival können Teilnehmer zwischen zwei verschiedenen Veranstaltungen wählen. Erfahrungsgemäß besuchen $36\,\%$ aller Teilnehmer die Beachparty, während alle anderen zum Rockkonzert gehen.
Die Tickets für das Festival kann man entweder online oder an der Abendkasse kaufen. Langjährige Erfahrungswerte zeigen, dass die Teilnehmer der Beachparty zu $70\,\%$ ihr Ticket online erwerben. Außerdem weiß man, dass insgesamt $26,8\,\%$ aller Teilnehmer ihr Ticket an der Abendkasse kaufen.

1.1

Berechne jeweils die Wahrscheinlichkeit für folgende Ereignisse.

$E_1$ : Von $5$ zufällig ausgewählten Teilnehmern besuchen alle die Beachparty.

$E_2$ : Von $30$ zufällig ausgewählten Teilnehmern gehen mindestens $20$ zur Beachparty.

$E_3$ : Von $1000$ Teilnehmern des Festivals besuchen mindestens $380$ , jedoch höchstens $390$ Leute die Beachparty.

1.2

Berechne die Wahrscheinlichkeit, dass ein Teilnehmer das Rockkonzert besucht und sein Ticket online erwirbt.

Ein Teilnehmer hat sein Ticket online erworben.
Berechne die Wahrscheinlichkeit, dass er dann Teilnehmer der Beachparty ist.

1.3

Für die Beachparty im Sommer $2020$ stehen $1500$ Tickets zur Verfügung.
Mit einer Wahrscheinlichkeit von mindestens $99\,\%$ sollen alle der am Festival Interessierten, die zur Beachparty gehen möchten, tatsächlich ein Ticket für die Beachparty erhalten. Ein Schüler behauptet, dass somit die Anzahl $n$ aller am Festival Interessierten unter $3980$ liegen muss.

Überprüfe diese Behauptung und ermittle den maximalen Wert für $n$ .

1.1

Die Zufallsgröße $X$ beschreibt die Anzahl der Teilnehmer, die zur Beachparty gehen.

Bei $E_1$ ist $X$ binomialverteilt mit $n=5$ und $p=0,36$ .

$\begin{array}[t]{rll} P(E_1)&=&P(X=5) \\[5pt] &=&0,36^5 \\[5pt] &\approx&0,006 \\[5pt] &\approx&0,6 \,\% \end{array}$

Bei $E_2$ ist $X$ binomialverteilt mit $n=30$ und $p=0,36$ .

$\begin{array}[t]{rll} P(E_2)&=&P(X\geq20)\\[5pt] &=&1-P(X\leq19) \\[5pt] &\approx&1-0,9994\\[5pt] &\approx&0,0006 \\[5pt] &\approx&0,06\,\% \end{array}$

Bei $E_3$ ist $X$ binomialverteilt mit $n=1000$ und $p=0,36$ .

$\begin{array}[t]{rll} P(E_3)&=&P(380\leq X\leq390) \\[5pt] &=&P(X\leq390)-P(X\leq379) \\[5pt] &\approx&0,9773-0,9002 \\[5pt] &\approx&0,0771 \\[5pt] &\approx&7,71\,\% \end{array}$

1.2

$B:$ Beachparty
$R:$ Rockkonzert

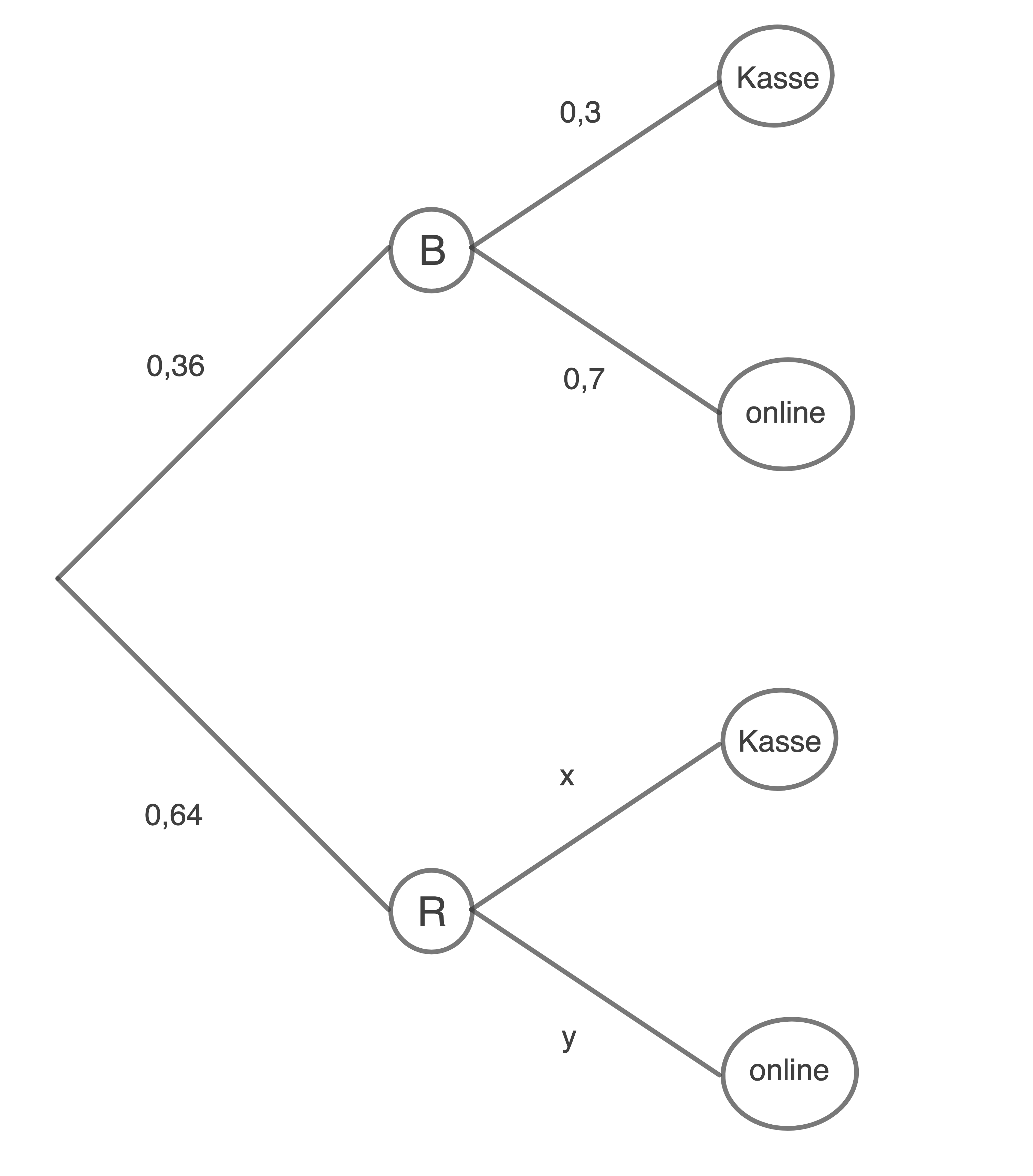
Diagramm mit Entscheidungsbaum und Wahrscheinlichkeiten für Kasse und Online-Zahlungen.

$P($ Ticket Kasse $)=0,268$

$\begin{array}[t]{rll} 0,268&=&0,36 \cdot 0,3+0,64 \cdot x \\[5pt] x&=&0,25 \end{array}$

$y=1-x=1-0,25=0,75$

$E_1:$ Ein Teilnehmer besucht das Rockkonzert und erwirbt sein Ticket online.

$P(E_1)=0,64 \cdot 0,75=0,48=48\,\%$

$E_2:$ Ein Teilnehmer, der sein Ticket online erworben hat besucht die Beachparty.

Bedingte Wahrscheinlichkeit:

$34,43\,\%$

Vollständige Lösung anzeigen

1.3

Die Zufallsgröße $X$ beschreibt die Anzahl der Teilnehmer, die zur Beachparty gehen.

$X$ ist binomialverteilt mit unbekanntem $n$ und $p=0,36$ .

Da $P(X\leq1500)\geq0,99$ gelten muss, kann man eine Tabelle erstellen, um den maximalen Wert für $n$ herauszufinden.

n	P(X)
3977	0,98827
3976	0,98864
3975	0,98899
3974	0,98934
3973	0,98968
3972	0,99001
3971	0,99032

Anhand der Tabelle sieht man, dass der maximale Wert $n=3972$ ist.

Da die maximale Teilnehmeranzahl $3972$ beträgt, liegt der Wert deutlich unter $3980$ und somit hat der Schüler Recht.
Der maximale Wert des Schülers kann auch noch kleiner gewählt werden.