Lineare Algebra

Aufgabe III 1.1

Die drei Punkte $P(-1 \mid 0 \mid -6),$ $Q(0 \mid -1 \mid 0)$ und $R(0 \mid 0 \mid -2)$ liegen in der Ebene $E.$ Die Gerade $g$ ist gegeben durch $g:\overrightarrow{x} = \pmatrix{-2 \\ 3 \\ 0} + s \cdot \pmatrix{3 \\ 0 \\ -4}; \;$ $s \in \mathbb{R}.$

Gib eine Gleichung der Ebene $E$ an.

(2 BE)

Ermittle den Spurpunkt der Ebene $E$ mit der $x_1$ -Achse.

(1 BE)

Gib die besondere Lage der Geraden $g$ im Koordinatensystem an und begründe deine Angabe.

(2 BE)

Berechne den Winkel, unter dem die Gerade $g$ die $x_1x_2$ -Ebene durchstößt.

(3 BE)

Gib die Koordinaten des Punktes $S$ an, in dem die Gerade $g$ die $x_1x_2$ -Ebene durchstößt.

Der Punkt $T(1 \mid 3 \mid -4)$ liegt in der Ebene $E.$ Der Punkt $U$ entsteht durch senkrechte Projektion des Punktes $T$ auf die $x_1x_2$ -Ebene.

Ermittle den Flächeninhalt des Dreiecks $STU.$

(3 BE)

Aufgabe III 1.2

Gegeben sind die Punkte $A(-1 \mid 7 \mid 6),$ $B(1 \mid 3 \mid 8),$ $C(-3 \mid -9 \mid -1)$ und $D(-5 \mid -5 \mid -3).$

Zeige, dass die Punkte $A, B, C$ und $D$ ein Parallelogramm, aber kein Rechteck bilden.

(4 BE)

$M$ ist der Mittelpunkt der Strecke $AB$ und $N$ ist der Mittelpunkt der Strecke $BC.$

Zeige, dass der Schnittpunkt der Strecken $DM$ und $AN$ die Strecke $DM$ im Verhältnis $4:1$ teilt.

(5 BE)

Aufgabe III 2

Im mittelamerikanischen Regenwald wird eine neu entdeckte Pyramide vermessen. Die Eckpunkte der Grundfläche sind $A(20 \mid 40 \mid 0),$ $B(-60 \mid 20 \mid 0),$ $C(-40 \mid -60 \mid 0)$ und $D(40 \mid -40 \mid 0)$ . Die Spitze der Pyramide befindet sich bei $S(-10 \mid -10 \mid 25).$ Alle Angaben sind in Metern.

Zeichne die Pyramide in ein Koordinatensystem.

(4 BE)

Weise nach, dass die Grundfläche der Pyramide ein Quadrat ist.

(3 BE)

Zeige, dass sich die Spitze der Pyramide senkrecht über dem Mittelpunkt des Quadrats befindet.

(2 BE)

Beschreibe Schritt für Schritt, wie man die Inhalte der vier Seitenflächen der Pyramide mit den angegebenen Informationen und den Erkenntnissen aus den Teilaufgaben b) und c) berechnen kann.
(Hinweis: Die Berechnung selbst ist nicht notwendig.)

(4 BE)

Vom Mittelpunkt der Kante $AB$ aus verläuft ein kleiner Schacht zur Kante $CS.$ Ein einziges Mal im Jahr scheint die Sonne durch diesen Schacht hindurch, d.h. die Sonnenstrahlen sind parallel zum Schacht. In diesem Fall haben die Strahlen die Richtung des Vektors $\overrightarrow{v}:$

$\overrightarrow{v} = \pmatrix{14 \\ 80 \\ -5}.$

Ermittle den Punkt auf der Kante $CS,$ an dem der Schacht aus der Pyramide austritt.

(4 BE)

Berechne den Steigungswinkel des Schachtes.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Aufgabe III 1.1

$\overrightarrow{PQ}=\pmatrix{0-(-1)\\-1-0\\0-(-6)}=\pmatrix{1\\-1\\6}$

$\overrightarrow{PR}=\pmatrix{0-(-1)\\0-0\\-2-(-6)}=\pmatrix{1\\0\\4}$

Damit ergibt sich die folgende Ebenengleichung:

$E:\overrightarrow{x}=\pmatrix{-1\\0\\-6}+s\cdot \pmatrix{1\\-1\\6}+t\cdot \pmatrix{1\\0\\4}$

Gesucht ist der Wert für $x_1,$ für den gilt:

$\pmatrix{x_1\\0\\0}=\pmatrix{-1\\0\\-6}+s\cdot \pmatrix{1\\-1\\6}+t\cdot \pmatrix{1\\0\\4}$

Es ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&x_1&=& -1+s+t &\quad \\ \text{II}\quad&0&=&-s &\quad \\ \text{III}\quad&0&=&-6+6s+4t &\quad \\ \end{array}$

Aus Gleichung $\text{II}$ folgt direkt $s=0.$ Einsetzen in Gleichung $\text{III}$ liefert:

$\begin{array}[t]{rll} 0&=&-6+4t &\quad \scriptsize \mid\;+6 \\[5pt] 6&=&4t &\quad \scriptsize \mid\;:4 \\[5pt] \dfrac{3}{2}&=&t \end{array}$

Einsetzen dieser beiden Werte in Gleichung $\text{I}$ ergibt nun:

$x_1=-1+0+\dfrac{3}{2}=\dfrac{1}{2}$

Der gesuchte Spurpunkt hat somit die Koordinaten $\left(\dfrac{1}{2}\,\bigg \vert \,0\,\bigg \vert \,0\right).$

Da der Richtungsvektor der Geraden $g$ die $x_2$ -Koordinate $0$ besitzt, besitzen alle Punkte auf $g$ die selbe $y$ -Koordinate. Damit verläuft die Gerade parallel zur $x_1x_3$ -Ebene.

Die $x_1 x_2$ -Ebene ist definiert durch $x_3=0$ . Der Normalenvektor dieser Ebene ist:

$\overrightarrow{n}=\pmatrix{0\\0\\1}$

Der Winkel $\alpha$ zwischen der Geraden $g$ und der Ebene wird wie folgt berechnet:

Rechenweg anzeigen

$\alpha\approx 53,13^\circ$

Koordianten von $\boldsymbol{S}$ angeben

Die $x_1x_2$ -Ebene ist definiert durch $x_3 = 0 .$ Einsetzen von $x_3 = 0$ in die Geradengleichung liefert:

$\begin{array}[t]{rll} 0+s\cdot (-4)&=& 0 \\[5pt] -4s&=& 0 &\quad \scriptsize \mid\; :(-4) \\[5pt] s&=& 0 \end{array}$

Einsetzen von $s = 0$ in die Geradengleichung:

$\overrightarrow{OS}=\pmatrix{-2\\3\\0}+0\cdot \pmatrix{3\\0\\-4}=\pmatrix{-2\\3\\0}$

Somit ist $S(-2 \mid 3 \mid 0)$ der Punkt, in dem die Gerade $g$ die $x_1x_2$ -Ebene durchstößt.

Flächeninhalt des Dreiecks ermitteln

Bei einer senkrechten Projektion auf die $x_1x_2$ -Ebene bleiben die $x_1$ - und $x_2$ -Koordinate gleich, während die $x_3$ -Koordinate Null wird. Damit gilt $U(1 \mid 3 \mid 0).$ Es folgt:

$\overrightarrow{ST} = \pmatrix{1 - (-2) \\ 3 - 3 \\ -4 - 0} = \pmatrix{ 3 \\ 0 \\ -4 }$

$\overrightarrow{SU} = \pmatrix{ 1 - (-2) \\ 3 - 3 \\ 0 - 0 } = \pmatrix{ 3 \\ 0 \\ 0}$

Berechnen des Kreuzprodukts:

$\overrightarrow{ST} \times \overrightarrow{SU} = \pmatrix{ 0 \cdot 0 - (-4) \cdot 0 \\ (-4) \cdot 3-3 \cdot 0\\ 3 \cdot 0 - 0 \cdot 3 } = \pmatrix{ 0 \\ -12 \\ 0}$

Somit gilt $|\overrightarrow{ST} \times \overrightarrow{SU}|= 12.$ Der Flächeninhalt $A$ des Dreiecks $STU$ lässt sich damit wie folgt berechnen:

$A = \dfrac{1}{2} \cdot |\overrightarrow{ST} \times \overrightarrow{SU}| = \dfrac{1}{2} \cdot 12 = 6.$

Der Flächeninhalt des Dreiecks beträgt $6$ Flächeneinheiten.

Aufgabe III 1.2

$\overrightarrow{A B}=\left(\begin{array}{c}1-(-1) \\ 3-7 \\ 8-6\end{array}\right)=\left(\begin{array}{c}2 \\ -4 \\ 2\end{array}\right)$

$\overrightarrow{C D}=\left(\begin{array}{c}-5-(-3) \\ -5-(-9) \\ -3-(-1)\end{array}\right)=\left(\begin{array}{c}-2 \\ 4 \\ -2\end{array}\right)$

Da $\overrightarrow{A B}=-\overrightarrow{C D}$ gilt, sind die Kanten $\overline{A B}$ und $\overline{C D}$ parallel.

$\overrightarrow{A D}=\left(\begin{array}{c}-5-(-1) \\ -5-7 \\ -3-6\end{array}\right)=\left(\begin{array}{c}-4 \\ -12 \\ -9\end{array}\right)$

$\overrightarrow{B C}=\left(\begin{array}{l}-3-1 \\ -9-3 \\ -1-8\end{array}\right)=\left(\begin{array}{c}-4 \\ -12 \\ -9\end{array}\right)$

Da $\overrightarrow{A D}=\overrightarrow{B C}$ gilt, sind die beiden anderen Kanten ebenfalls parallel. Da beide Paare von gegenüberliegenden Seiten parallel sind, bilden die Punkte somit ein Parallelogramm. Weiter gilt:

Rechenweg anzeigen

$\overrightarrow{A B} \circ \overrightarrow{A D} \neq 0$

Da in einem Rechteck alle Winkel rechte Winkel sein müssen, kann es sich folglich nicht um ein solches handeln.

Koordinaten der Mittelpunkte $M$ und $N$ berechnen:

$M\left(\dfrac{-1+1}{2}, \dfrac{7+3}{2}, \dfrac{6+8}{2}\right)$ $=M(0\mid 5\mid 7)$

$N\left(\dfrac{1+(-3)}{2}, \dfrac{3+(-9)}{2}, \dfrac{8+(-1)}{2}\right)$ $=N(-1\mid -3\mid 3,5)$

Parametergleichungen der Strecken $DM$ und $AN$ bestimmen:

Für $0\leq t\leq 1$ bzw. $0\leq s\leq 1$ werden die Strecken $DM$ bzw. $AN$ wie folgt dargestellt:

Rechenweg anzeigen

$\overrightarrow{OD}+t\cdot \overrightarrow{DM} = \left(\begin{array}{l}-5 \\ -5 \\ -3\end{array}\right)+t \cdot\left(\begin{array}{c}5 \\ 10 \\ 10\end{array}\right)$

Rechenweg anzeigen

$\overrightarrow{OA}+s\cdot \overrightarrow{AN} = \left(\begin{array}{c}-1 \\ 7 \\ 6\end{array}\right)+s \cdot\left(\begin{array}{c}0 \\ -10 \\ -2,5\end{array}\right)$

Um den Schnittpunkt zu berechnen, werden die beiden Parametergleichungen gleichgesetzt:

$\left(\begin{array}{l}-5 \\ -5 \\ -3\end{array}\right)+t \cdot\left(\begin{array}{c}5 \\ 10 \\ 10\end{array}\right)$ $=\left(\begin{array}{c}-1 \\ 7 \\ 6\end{array}\right)+s \cdot\left(\begin{array}{c}0 \\ -10 \\ -2,5\end{array}\right)$

Aus der ersten Zeile folgt:

$\begin{array}[t]{rll} -5+5t&=& -1+s\cdot 0 &\quad \scriptsize \mid\;+5 \\[5pt] 5t&=& 4 &\quad \scriptsize \mid\; :5 \\[5pt] t&=& \dfrac{4}{5} \end{array}$

Da $t=\frac{4}{5}$ ist, wird $D M$ in einem Verhältnis von 4 zu 1 geteilt, da $t$ den Anteil der Strecke $DM$ beschreibt, der zwischen $D$ und dem Schnittpunkt der beiden betrachteten Strecken liegt.

Aufgabe III 2

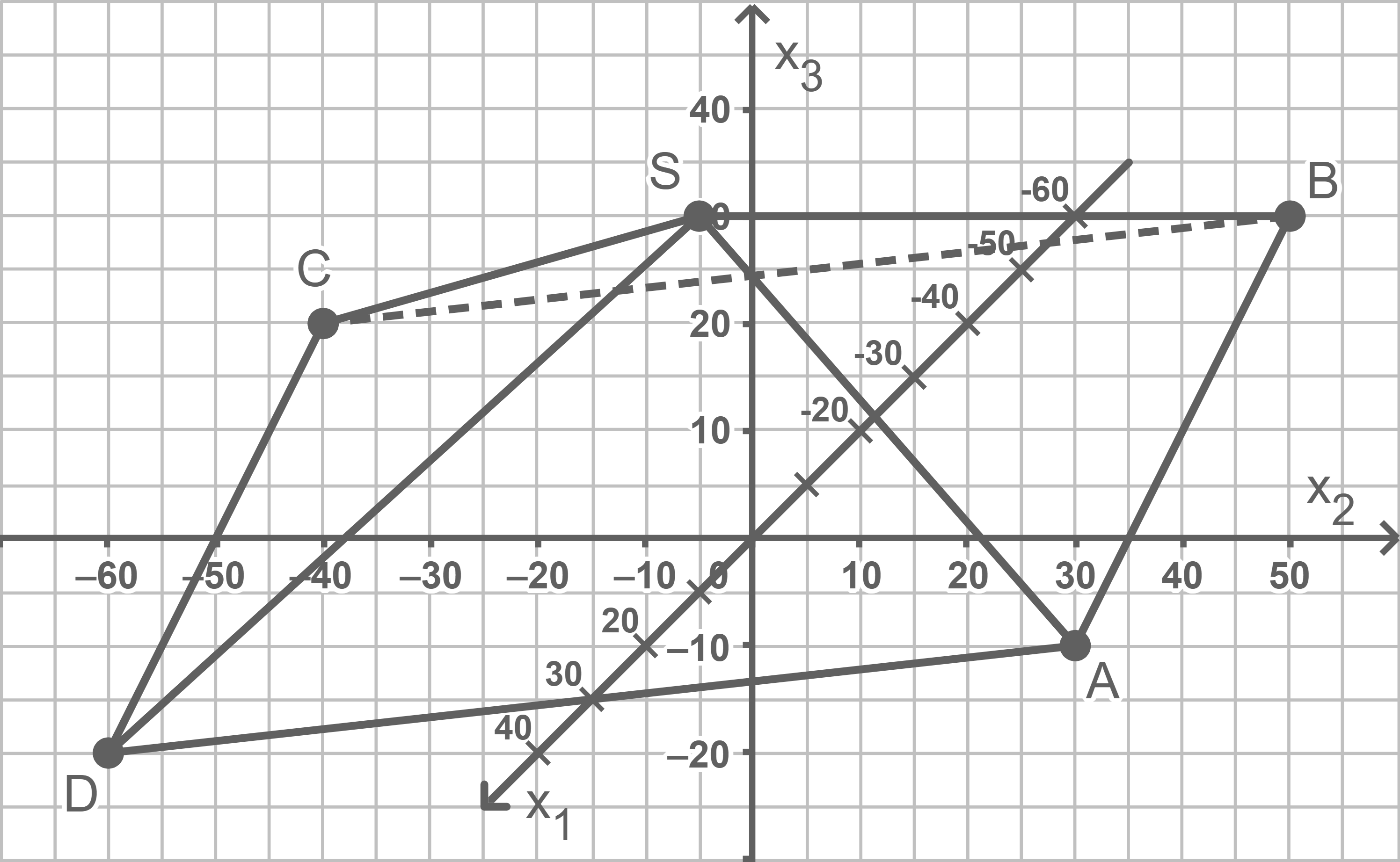
Graph mit Punkten A, B, C, D und S auf einem Koordinatensystem mit Achsen x1, x2 und x3.

$\overrightarrow{AB} = \pmatrix{-60 - 20 \\ 20 - 40 \\ 0 - 0} = \pmatrix{-80 \\ -20 \\ 0}$

$\overrightarrow{BC} = \pmatrix{-40 - (-60) \\ -60 - 20 \\ 0 - 0} = \pmatrix{20 \\ -80 \\ 0}$

$\overrightarrow{CD} = \pmatrix{40 - (-40) \\ -40 - (-60) \\ 0 - 0} = \pmatrix{80 \\ 20 \\ 0}$

$\overrightarrow{DA} = \pmatrix{20 - 40 \\ 40 - (-40) \\ 0 - 0} = \pmatrix{-20 \\ 80 \\ 0}$

Da $\overrightarrow{AB}=-\overrightarrow{CD}$ und $\overrightarrow{BC}=-\overrightarrow{DA}$ gilt, sind die gegenüberliegenden Seiten der Grundfläche parallel zueinander.

$|\overrightarrow{AB}| = \sqrt{(-80)^2 + (-20)^2 + 0^2}$ $=\sqrt{6800}$

$|\overrightarrow{BC}| = \sqrt{20^2 + (-80)^2 + 0^2}= \sqrt{6800}$

$|\overrightarrow{CD}| = \sqrt{80^2 + 20^2 + 0^2} = \sqrt{6800}$

$|\overrightarrow{DA}| = \sqrt{(-20)^2 + 80^2 + 0^2} = \sqrt{6800}$

Alle Seitenlängen der Grundfläche sind außerdem gleich lang.

$\overrightarrow{AB} \circ \overrightarrow{BC} = -80 \cdot 20 + (-20) \cdot (-80)$ $+ 0 \cdot 0 = 0$

Die Grundfläche hat somit einen rechten Winkel. Aufgrund der restlichen bereits gezeigten Eigenschaften müssen folglich alle Winkel $90^\circ$ betragen und die Grundfläche ist ein Quadrat.

Mittelpunkt des Quadrats berechnen:

$\begin{array}[t]{rll} \overrightarrow{OM}&=& \overrightarrow{OA}+\dfrac{1}{2}\cdot\overrightarrow{AC} \\[5pt] &=& \pmatrix{20\\40\\0}+\dfrac{1}{2}\cdot \pmatrix{-60\\-100\\0} \\[5pt] &=& \pmatrix{-10\\-10\\0} \end{array}$

Der Mittelpunkt des Quadrats hat also die Koordinaten $M(-10\mid -10\mid 0)$ und unterscheidet sich vom Punkt $S$ somit nur in der $x_3$ -Koordinate. Damit befindet sich die Spitze der Pyramide senkrecht über dem Mittelpunkt des Quadrats.

1. Schritt: Länge der Grundseiten der Seitenflächen berechnen

Die Länge der Grundseiten $g_S$ wurde bereits in Teilaufgabe b) berechnet. Da die Grundfläche quadratisch ist, sind die Grundseiten aller Seitenflächen gleich lang.

2. Schritt: Höhe der Seitenflächen berechnen

Da die Spitze der Pyramide senkrecht über dem Mittelpunkt des Quadrats ist, sind alle dreieckigen Seitenflächen gleich groß und haben die gleiche Höhe $h_S.$ Diese kann berechnet werden, indem der Betrag des Verbindungsvektors des Mittelpunkts einer der Grundseiten mit der Spitze der Pyramide berechnet wird.

3. Schritt: Flächeninhalt berechnen

Mit der Formel für den Flächeninhalt eines Dreiecks kann nun der Flächeninhalt aller Seitenflächen der Pyramide zusammen berechnet werden:

$A=4\cdot \dfrac{1}{2}\cdot g_s\cdot h_s$

Mittelpunkt der Kante $AB$ berechnen:

$M_{AB}\left(\dfrac{20+(-60)}{2}, \dfrac{40+20}{2}, \dfrac{0+0}{2}\right)$ $=M_{AB}(-20\mid 30\mid 0)$

Der Schacht verläuft durch den Punkt $M_{A B}$ in Richtung des Vektors $\vec{v}=\left(\begin{array}{c}14 \\ 80 \\ -5\end{array}\right)$ . Die Parametergleichung der Geraden, die den Schacht beschreibt, lautet somit:

$g:\overrightarrow{x}=\pmatrix{-20\\30\\0}+t\cdot \pmatrix{14\\80\\-5}$

Die Kante $CS$ lässt sich für $0\leq s\leq 1$ durch die folgende Parametergleichung beschreiben:

$\overrightarrow{OC}+s\cdot \overrightarrow{CS}=\pmatrix{-40\\-60\\0}+s\cdot \pmatrix{30\\50\\25}$

Gleichsetzen der beiden Ausdrücke liefert folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&-20+14t&=& -40+30s &\quad \\ \text{II}\quad&30+80t&=&-60+50s &\quad \\ \text{III}\quad&-5t&=&25s &\quad \\ \end{array}$

Dividieren von Gleichung $\text{III}$ durch $-5$ liefert direkt $t=-5s.$ Einsetzen in Gleichung $\text{I}$ ergibt:

Rechenweg anzeigen

$s = \dfrac{1}{5}$

Einsetzen in die Gleichung der Kante $CS$ liefert für den Schnittpunkt $P:$

$\overrightarrow{OP}=\pmatrix{-40\\-60\\0}+\dfrac{1}{5}\cdot \pmatrix{30\\50\\25}=\pmatrix{-34\\-50\\5}$

Der Punkt, an dem der Schacht aus der Pyramide austritt, hat somit die Koordinaten $P(-34\mid -50\mid 5).$

Der Richtungsvektor des Schachtes ist durch den Vektor $\overrightarrow{v}$ gegeben. Der Steigungswinkel $\alpha$ gegenüber der $x_1x_2$ -Ebene wird wie folgt berechnet:

$\begin{array}[t]{rll} \tan (\alpha)&=& \dfrac{|x_3|}{\sqrt{x_1^2+x_2^2}} \\[5pt] \tan (\alpha)&=& \dfrac{|-5|}{\sqrt{14^2+80^2}} \\[5pt] \tan (\alpha)&=& \dfrac{5}{\sqrt{6596}} \quad \scriptsize \mid\;\tan^{-1} \\[5pt] \alpha&\approx& 3,53^\circ \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?