Vektorgeometrie
1
Ein Architekt plant ein modernes Museum.
Im Modell hat das Museum eine rechteckige Grundfläche mit den Eckpunkten
, 
, 
, 
und ein Dach, das aus den vier
Eckpunkten
, 
, 
, 
gebildet wird.
Die von der Grundfläche zum Dach verlaufenden Kanten des Modells verbinden Punkte gleichen Buchstabens, z.B. ist
mit 
verbunden.
Eine Längeneinheit im Modell entspricht
Meter 
.
Im Modell hat das Museum eine rechteckige Grundfläche mit den Eckpunkten
Eckpunkten
Die von der Grundfläche zum Dach verlaufenden Kanten des Modells verbinden Punkte gleichen Buchstabens, z.B. ist
Eine Längeneinheit im Modell entspricht
1.1
Zeichne das Modell in ein geeignetes Koordinatensystem.
4
1.2
Die Vorderseite des Modells (d.h. der Schnitt mit der Ebene 
) bildet ein Trapez.
Diese Fläche soll zu
aus einem Spezialglas bestehen, das 
pro 
kostet.
Berechne die hierfür zu kalkulierenden Kosten.
Diese Fläche soll zu
3
1.3
Die Kante 
teilt das Dach in zwei dreieckige Flächen.
Bestimme den Winkel, den diese beiden Flächen im Innern des Modells bilden.
4
1.4
Im Punkt 
soll ein Laser installiert werden, der den Laserstrahl in Richtung 
geradlinig in den Himmel schickt.
Entsprechend soll im Punkt
ein weiterer Laser mit Laserstrahl in Richtung 
installiert werden.
Entsprechend soll im Punkt
1.4.1
Gib für jeden der beiden Laserstrahlen eine Gleichung der entsprechenden Geraden an.
2
1.4.2
Bestimme die Höhe über der Grundfläche, in der diese beiden Laserstrahlen genau 
voneinander entfernt sind.
2
1.1
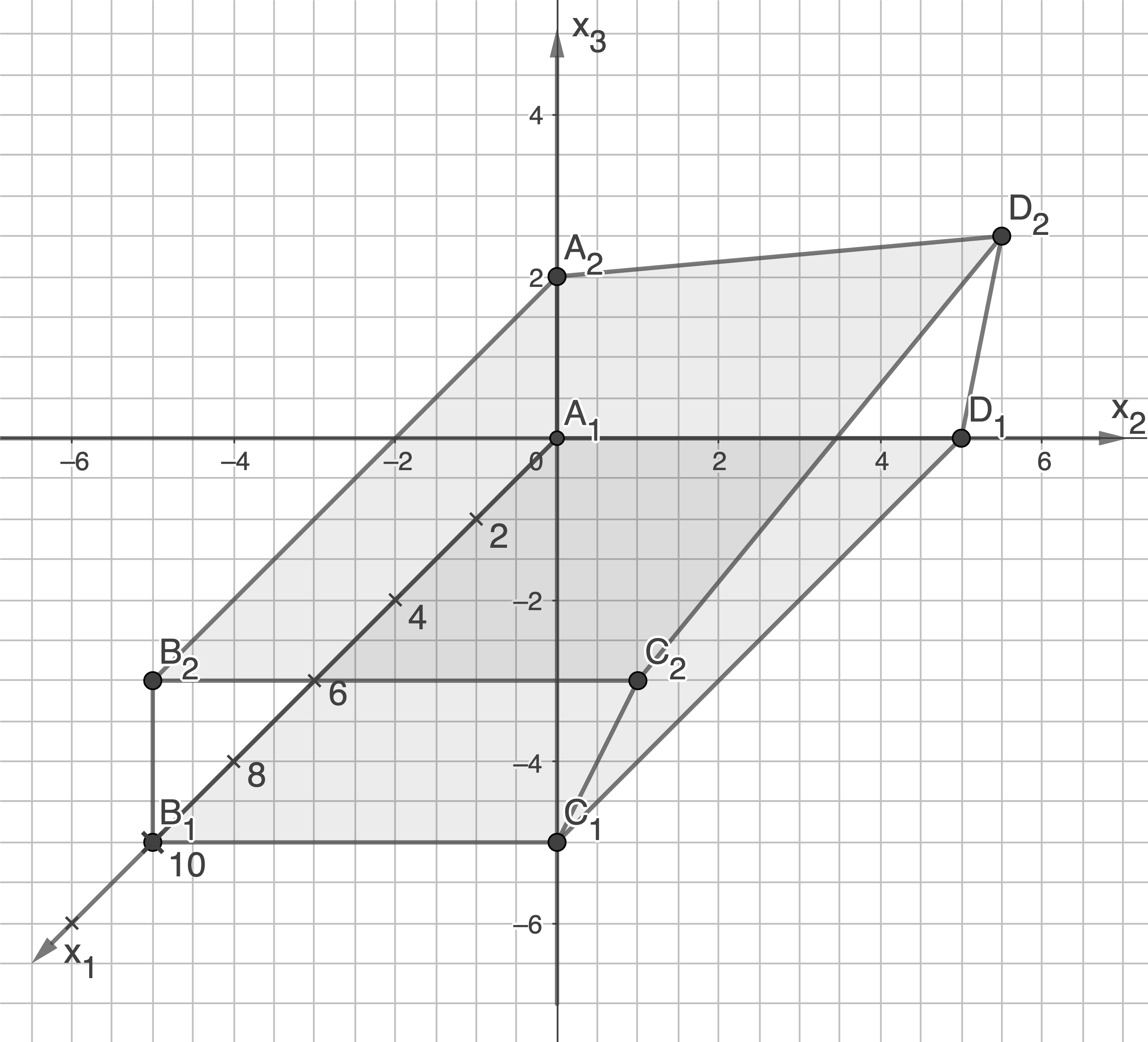
1.2
Flächeninhalt Trapez:
Länge der Strecke 
:
Länge der Strecke 
:
Länge der Strecke 
:
von 
:
Kosten:
Die Kosten für das Spezialglas betragen 
.
1.3
Ebenengleichung der 1. Fläche:
Normalenvektor: 
Ebenengleichung der 2. Fläche:
![\(\begin{array}[t]{rll}
E_2: \overrightarrow{x}&=&\overrightarrow{OA_2}+r \cdot \overrightarrow{A_2C_2}+s \cdot \overrightarrow{A_2D_2} \\[5pt]
&=&\pmatrix{0\\0\\2}+r \cdot \pmatrix{10\\6\\0}+s \cdot \pmatrix{0\\5,5\\0,5}
\end{array}\)](https://mathjax.schullv.de/266bb8b222270e82de9f2966971fa337500ebf088b9b8d8157915fd356a80052?color=5a5a5a)
Vektorprodukt:
Schnittwinkel:
![\(\begin{array}[t]{rll}
\cos(\alpha)&=&\dfrac{\mid\overrightarrow{n_{E_1}} \cdot \overrightarrow{n_{E_2}}\mid}{\mid\overrightarrow{n_{E_1}}\mid \cdot \mid\overrightarrow{n_{E_2}}\mid} \\[5pt]
&=&\dfrac{\left|\pmatrix{0\\0\\1} \cdot \pmatrix{3\\-5\\55}\right|}{\sqrt{1^2} \cdot \sqrt{3^2+(-5)^2+55^2}} \\[5pt]
&=&\dfrac{55}{1 \cdot \sqrt{3059}} \\[5pt]
\alpha&\approx&6^{\circ}
\end{array}\)](https://mathjax.schullv.de/087fb8a3e63f4fefe8e1237ba550e67508ef1b83abf030439f76320395453698?color=5a5a5a)
Winkel im Inneren des Models:
Die beiden Flächen bilden einen Winkel von 
im Inneren des Models.
1.4.1
Laserstrahl 1:
Laserstrahl 2:
1.4.2
Vollständige Lösung anzeigen