Anwendungsorientierte Analysis 3
4.1
Ein Hersteller plant ein Zelt, dessen Gerüst aus neun Stangen besteht. Vier Stangen haben jeweils die Länge zwei Meter und die Länge der restlichen fünf Stangen (in Meter) wird mit 
bezeichnet (siehe Abbildung). Aus praktischen Gründen soll 
gelten.
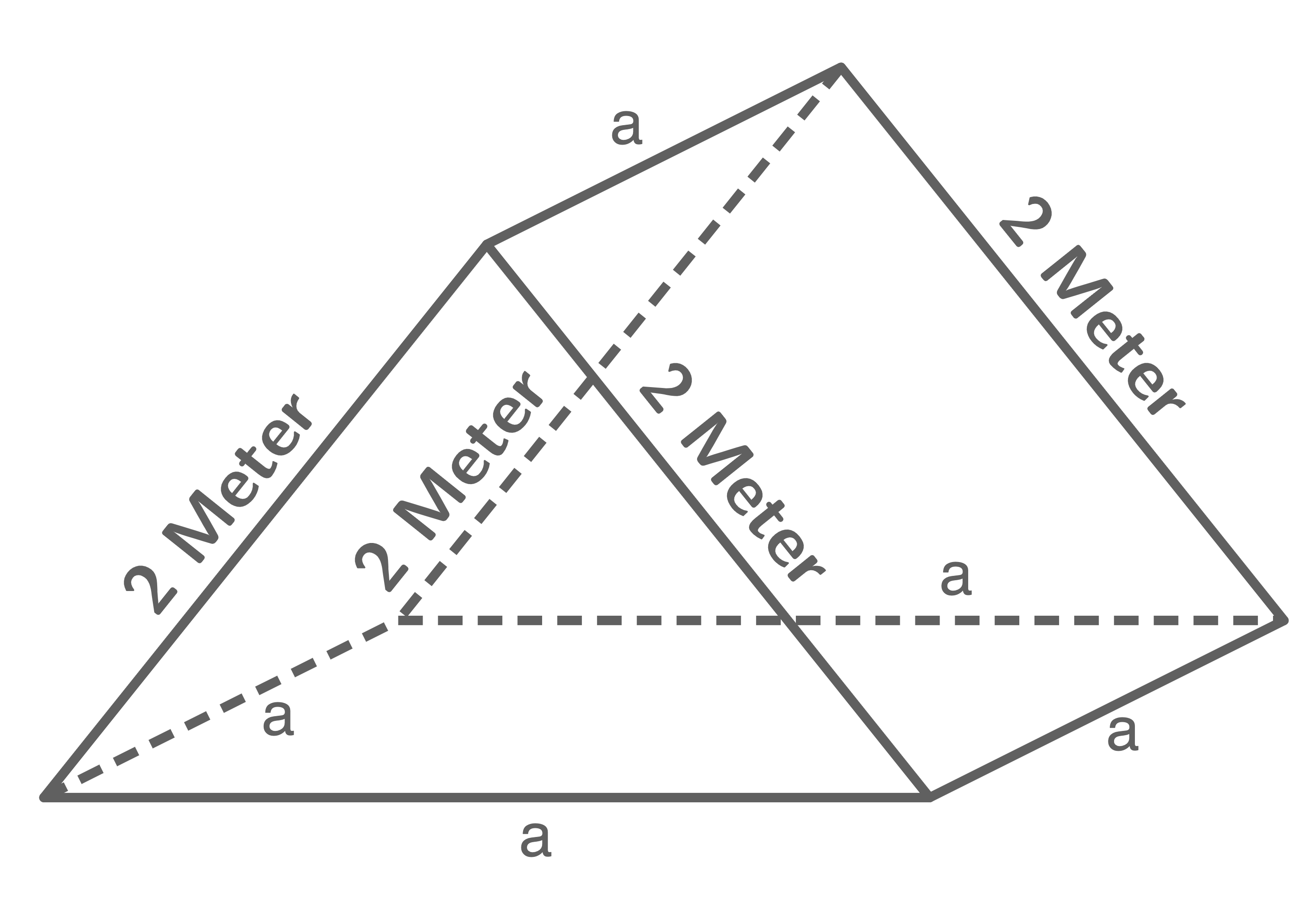
4.1.1
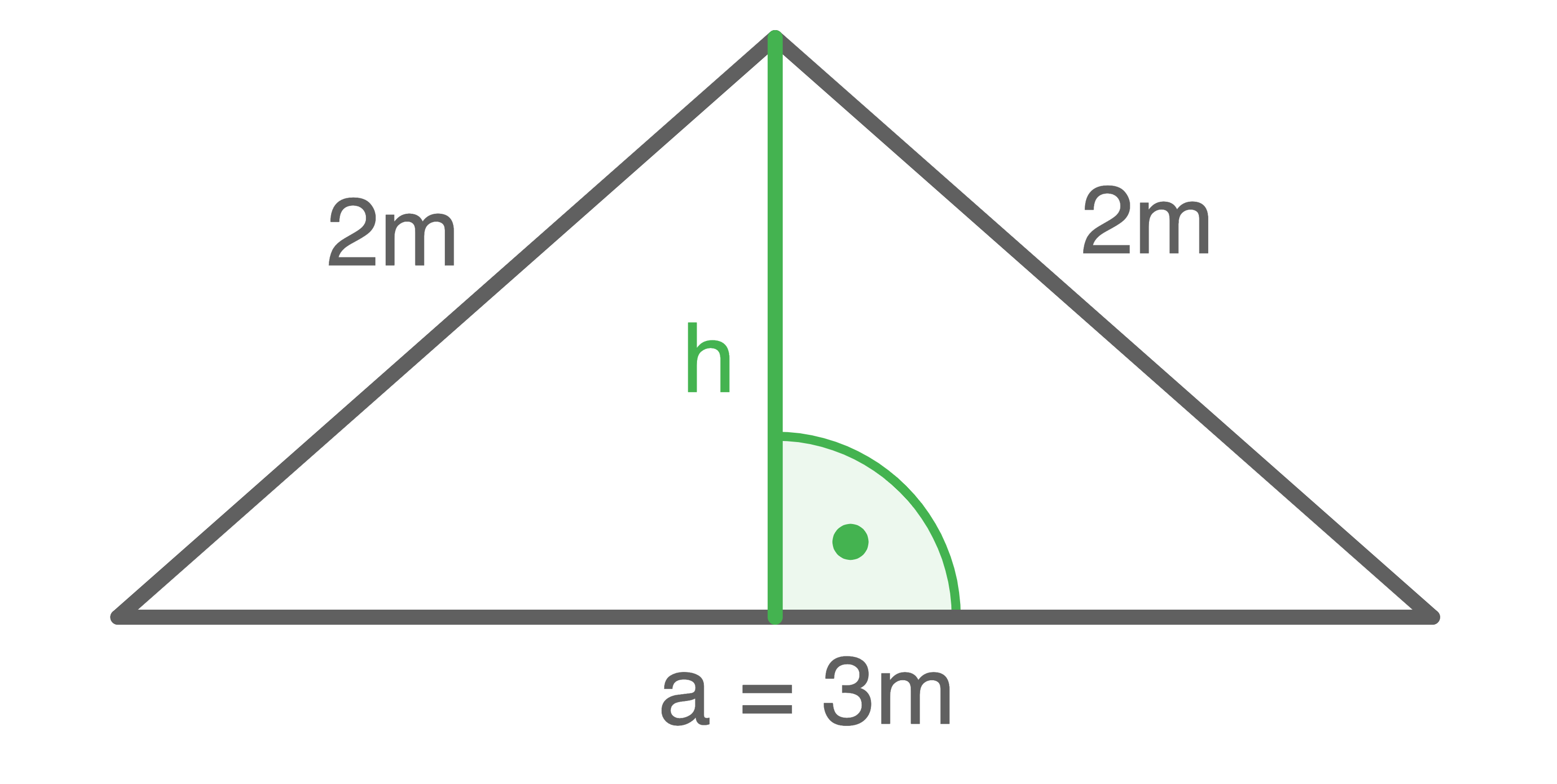
Berechne die Höhe des Zeltes für den Fall 
2
4.1.2
Die Funktion 
mit 
und 
beschreibt das Volumen des Zeltes in Abhängigkeit von 
nimmt an der gleichen Stelle wie 
den maximalen Wert an. Berechne den Wert von 
für den das Volumen des Zeltes maximal ist. Gib das maximale Volumen an.
5
4.2
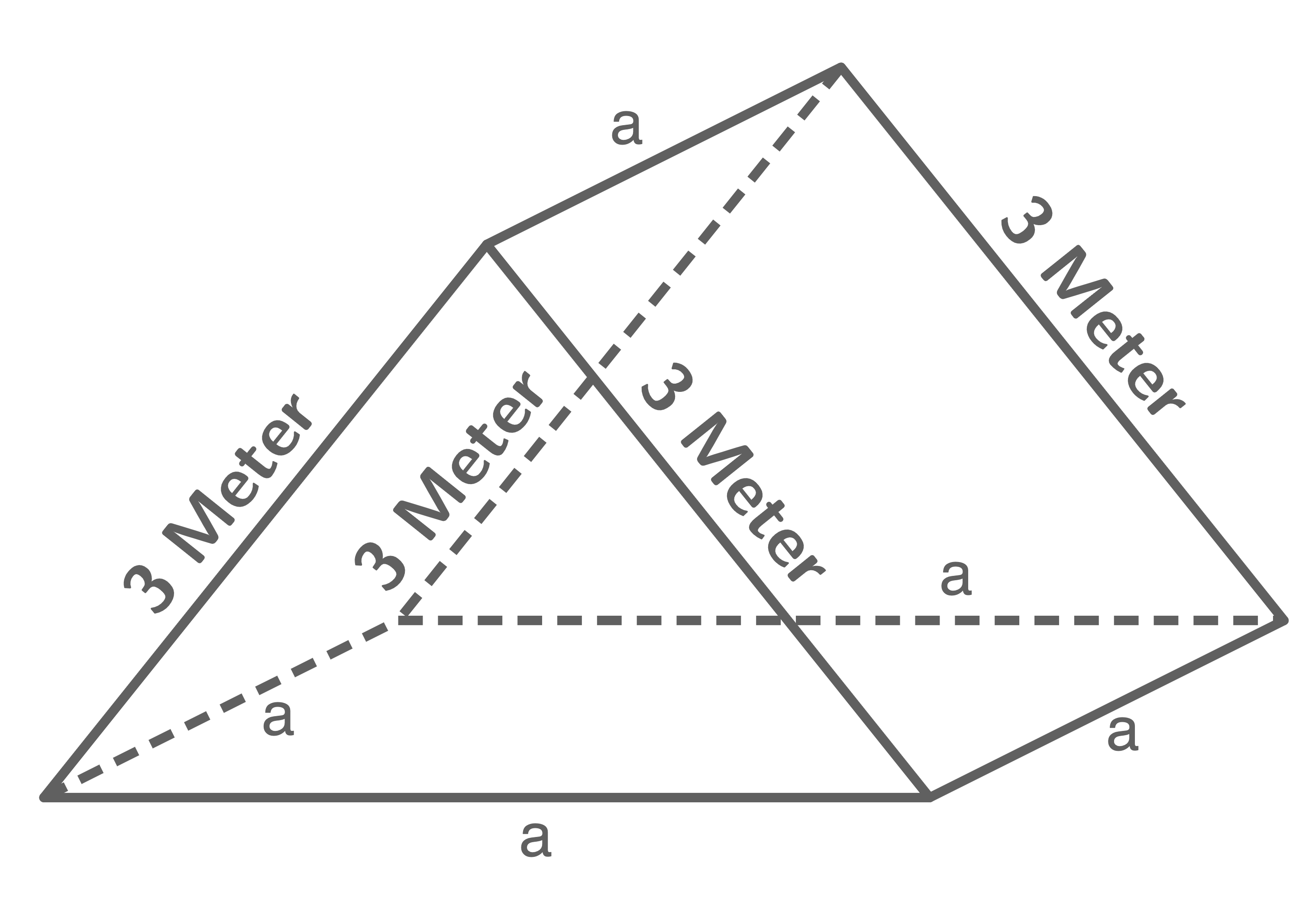
Für ein größeres Zelt werden die zwei Meter langen Stangen durch drei Meter lange Stangen ersetzt (siehe Abbildung).
Das Volumen dieses Zeltes kann durch den Term
berechnet werden.
Ermittle den Wert von
Das Volumen dieses Zeltes kann durch den Term
Ermittle den Wert von
3
10
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
4.1.1
4.1.2
Da an der gleichen Stelle wie den maximalen Wert annimmt, wird im Folgenden untersucht.
1. Schritt: Ableitungsfunktionen bestimmen
2. Schritt: Notwendiges Kriterium für Extremstellen anwenden
![\(\begin{array}[t]{rll}
E](https://mathjax.schullv.de/0be1d62705b5c2568a02bf82d4950a864123e9ddfe433b527ce9a6645bb7800f?color=5a5a5a)
Mit dem Satz vom Nullprodukt folgt, dass 
oder 
gelten muss, damit die Gleichung erfüllt ist. Also ist 
![\(\begin{array}[t]{rll}
4-\dfrac{3}{8}a^2 &=& 0 &\quad \scriptsize \mid\;+\frac{3}{8}a^2 \\[5pt]
4 &=& \dfrac{3}{8}a^2 &\quad \scriptsize \mid\; \cdot \frac{8}{3}\\[5pt]
\dfrac{32}{3} &=& a^2 &\quad \scriptsize \mid\; \sqrt{\;}\\[5pt]
\pm\sqrt{\dfrac{32}{3}} &=& a_{2,3}\\[5pt]
a_{2,3}&=& \pm\sqrt{\dfrac{32}{3}}
\end{array}\)](https://mathjax.schullv.de/7c36c375b2893e9ef2f996af8c5e0964ee4e3cabded552c75d653fdc92239053?color=5a5a5a)
Da negative Werte für und im Sachzusammenhang nicht relevant sind, wird im Folgenden 
weiterhin untersucht.
3. Schritt: Intervallränder vergleichen
Für 
nimmt und damit auch den maximalen Wert an.
Für 
ist das Volumen des Zeltes maximal. Das maximale Volumen beträgt ca. 
4.2
Das Zelt hat die Form eines Prismas mit dreieckiger Grundfläche 
und Höhe Daher gilt:
Die Höhe 
der Grundfläche kann in Abhängigkeit von wie in der ersten Aufgabe mit dem Satz des Pythagoras berechnet werden:
Für den Flächeninhalt der Grundfläche folgt damit:
![\(\begin{array}[t]{rll}
G &=& \dfrac{1}{2}\cdot a\cdot h \\[5pt]
&=& \dfrac{1}{2}\cdot a\cdot \sqrt{9 - \dfrac{1}{4}a^2} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/f3b1625efd703036cc5e9c1f86fd4295a058eb4ac95aec865c6dcb69a19dac85?color=5a5a5a)
Für das Volumen ergibt sich:
![\(\begin{array}[t]{rll}
V &=& G\cdot a \\[5pt]
&=& \dfrac{1}{2}\cdot a\cdot \sqrt{9 - \dfrac{1}{4}a^2} \cdot a \\[5pt]
&=& \dfrac{1}{2}\cdot a^2\cdot \sqrt{9 - \dfrac{1}{4}a^2} \\[5pt]
&=& \sqrt{\dfrac{1}{4}\cdot a^4\left(9 - \dfrac{1}{4}a^2\right)} \\[5pt]
&=& \sqrt{\dfrac{9}{4}\cdot a^4 - \dfrac{1}{16}a^6} \\[5pt]
\end{array}\)](https://mathjax.schullv.de/df014b8fec4d14c2d7a464ce4a1cd151d83cbe7753c6e3976ceeb41e16e07aae?color=5a5a5a)
Also ist 