Analysis
Aufgabe I 1.1
Gegeben ist die in
a)
Einer der drei Graphen entspricht 
Beurteile für jeden Graphen, ob es sich um handeln kann.
handeln kann.
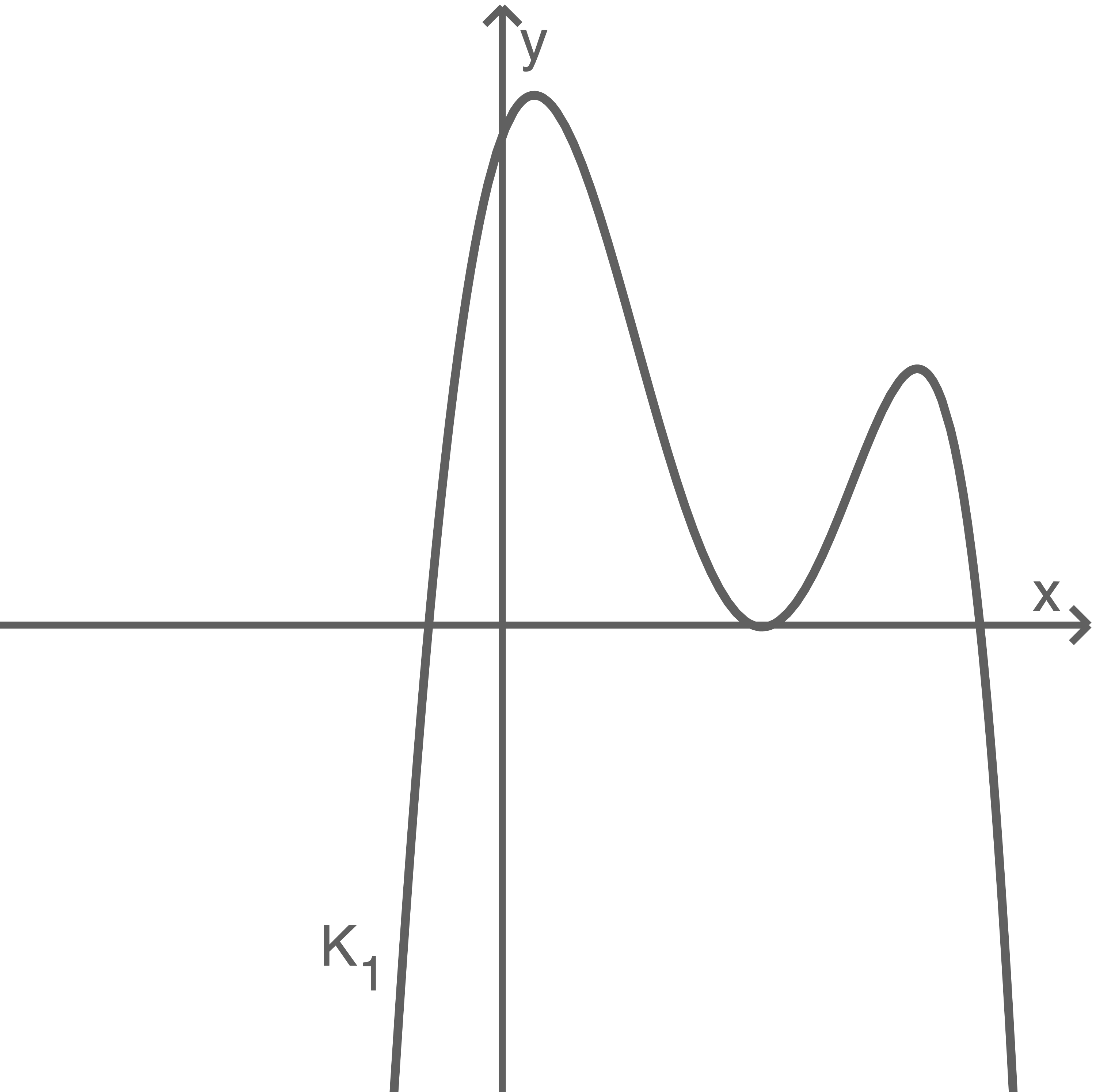
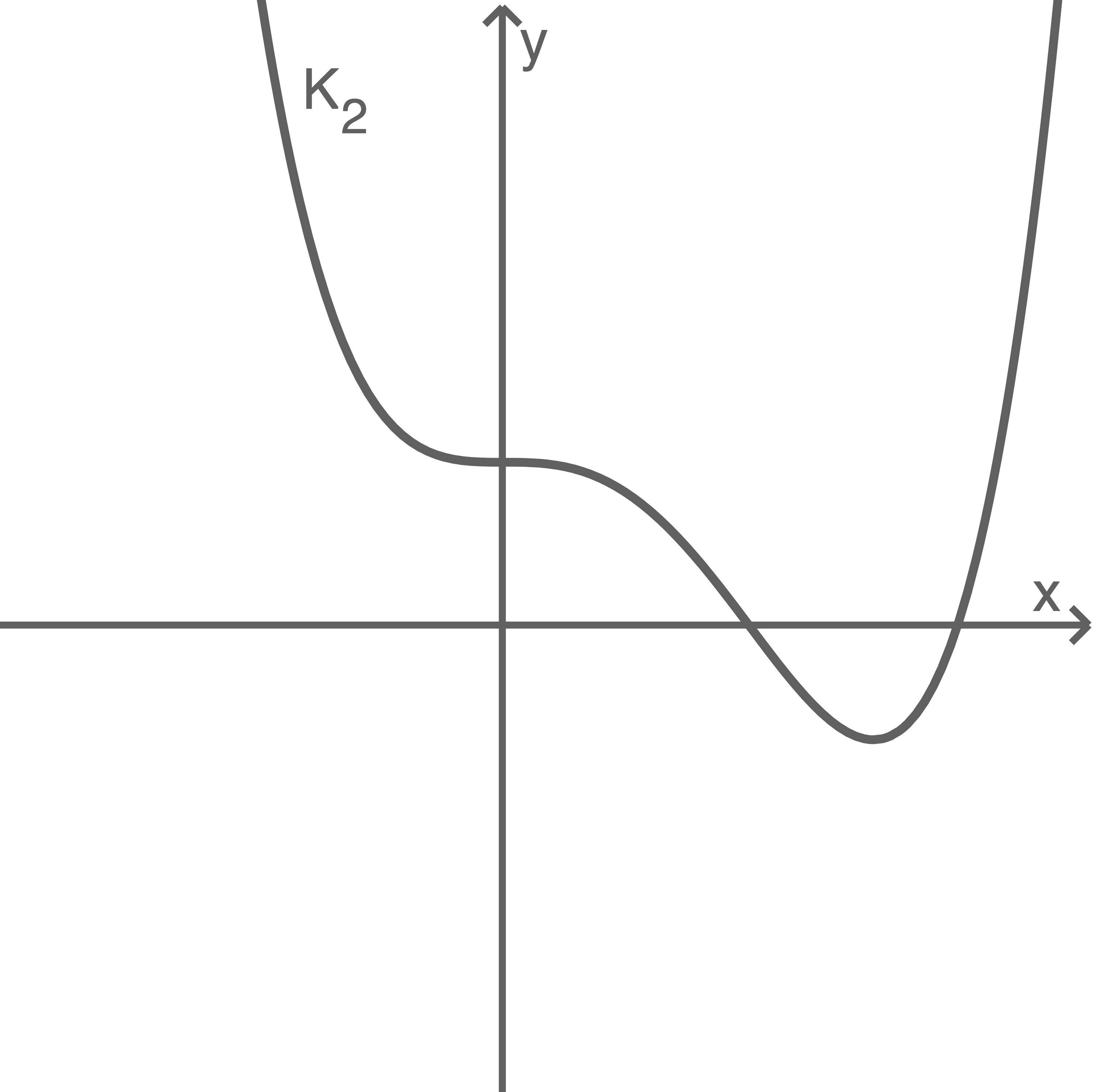
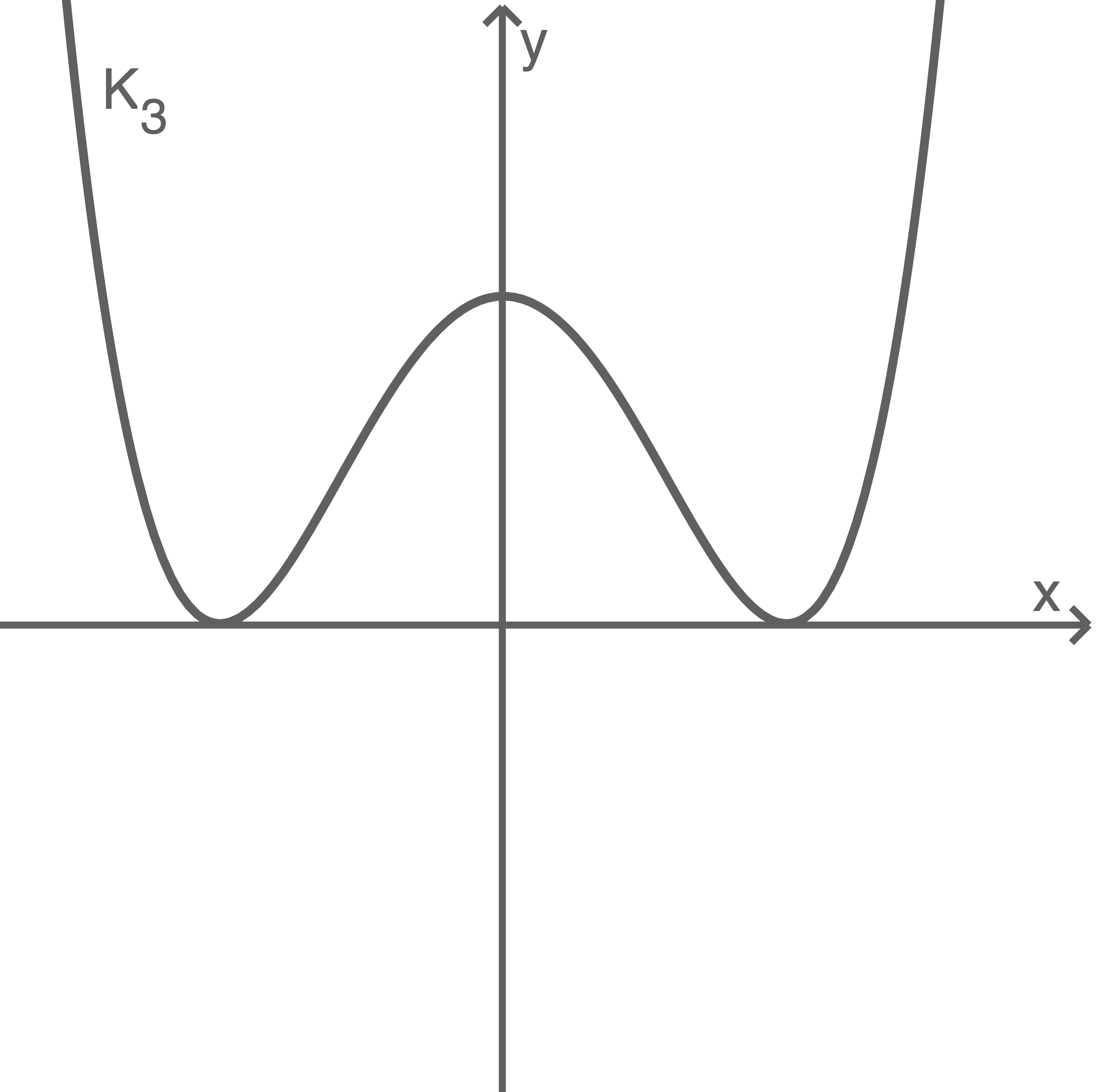
Beurteile für jeden Graphen, ob es sich um



(6 BE)
b)
Berechne die Koordinaten aller Punkte, in denen  eine waagerechte Tangente hat.
eine waagerechte Tangente hat.
Gib für jeden dieser Punkte an, ob es sich um einen Hoch-, Tief- oder Sattelpunkt handelt.
Gib für jeden dieser Punkte an, ob es sich um einen Hoch-, Tief- oder Sattelpunkt handelt.
(5 BE)
c)
Weise nach, dass  bei
bei  eine Nullstelle hat.
eine Nullstelle hat.
Neben dem Wendepunkt
(1 BE)
Der Punkt
d)
Weise nach, dass sich die beiden Wendetangenten im Punkt  schneiden.
schneiden.
(6 BE)
e)
Das Dreieck  wird von
wird von  in zwei Teile geteilt.
Berechne den Flächeninhalt der Teilfläche oberhalb von
in zwei Teile geteilt.
Berechne den Flächeninhalt der Teilfläche oberhalb von 
(4 BE)
Aufgabe I 1.2
Die  -Konzentration in der Atmosphäre wird seit 1958 durchgehend gemessen. Dabei sind die jährlichen Werte der Jahre 2012 bis 2022 in folgender Tabelle eingetragen. Die
-Konzentration in der Atmosphäre wird seit 1958 durchgehend gemessen. Dabei sind die jährlichen Werte der Jahre 2012 bis 2022 in folgender Tabelle eingetragen. Die  -Konzentration wird in Millionstel (ppm, „parts per million“) angegeben.
-Konzentration wird in Millionstel (ppm, „parts per million“) angegeben.
| Jahr | |
|---|---|
| 2012 | |
| 2013 | |
| 2014 | |
| 2015 | |
| 2016 | |
| 2017 | |
| 2018 | |
| 2019 | |
| 2020 | |
| 2021 | |
| 2022 |
Quelle:
Dr. Pieter Tans, NOAA/GGML and Dr. Ralph Keeling, Scripps Institution of Oceanography
URL: https://gml.noaa.gov/ccgg/trends/data.html, heruntergeladen am 15.05.2023
Dr. Pieter Tans, NOAA/GGML and Dr. Ralph Keeling, Scripps Institution of Oceanography
URL: https://gml.noaa.gov/ccgg/trends/data.html, heruntergeladen am 15.05.2023
a)
Bestimme die durchschnittliche Änderungsrate der  -Konzentration im Zeitraum 2012 bis 2022.
-Konzentration im Zeitraum 2012 bis 2022.
(2 BE)
b)
Ermittle ein mathematisches Modell für den gegebenen Verlauf der CO2-Konzentration. Gib dazu eine geeignete Funktionsgleichung an. Begründe deine Auswahl.
(6 BE)
c)
Berechne die CO2-Konzentration, die laut deinem Modell im Jahr 2100 zu erwarten ist.
(2 BE)
d)
Deute im Sachzusammenhang, warum ein mathematisches Modell, das auf Messungen innerhalb der Jahre 2012 bis 2022 beruht, nicht grundsätzlich für eine Vorhersage der CO2-Konzentration im Jahr 2100 verwendet werden kann.
(3 BE)
Aufgabe I 2.1
Für eine reelle Zahl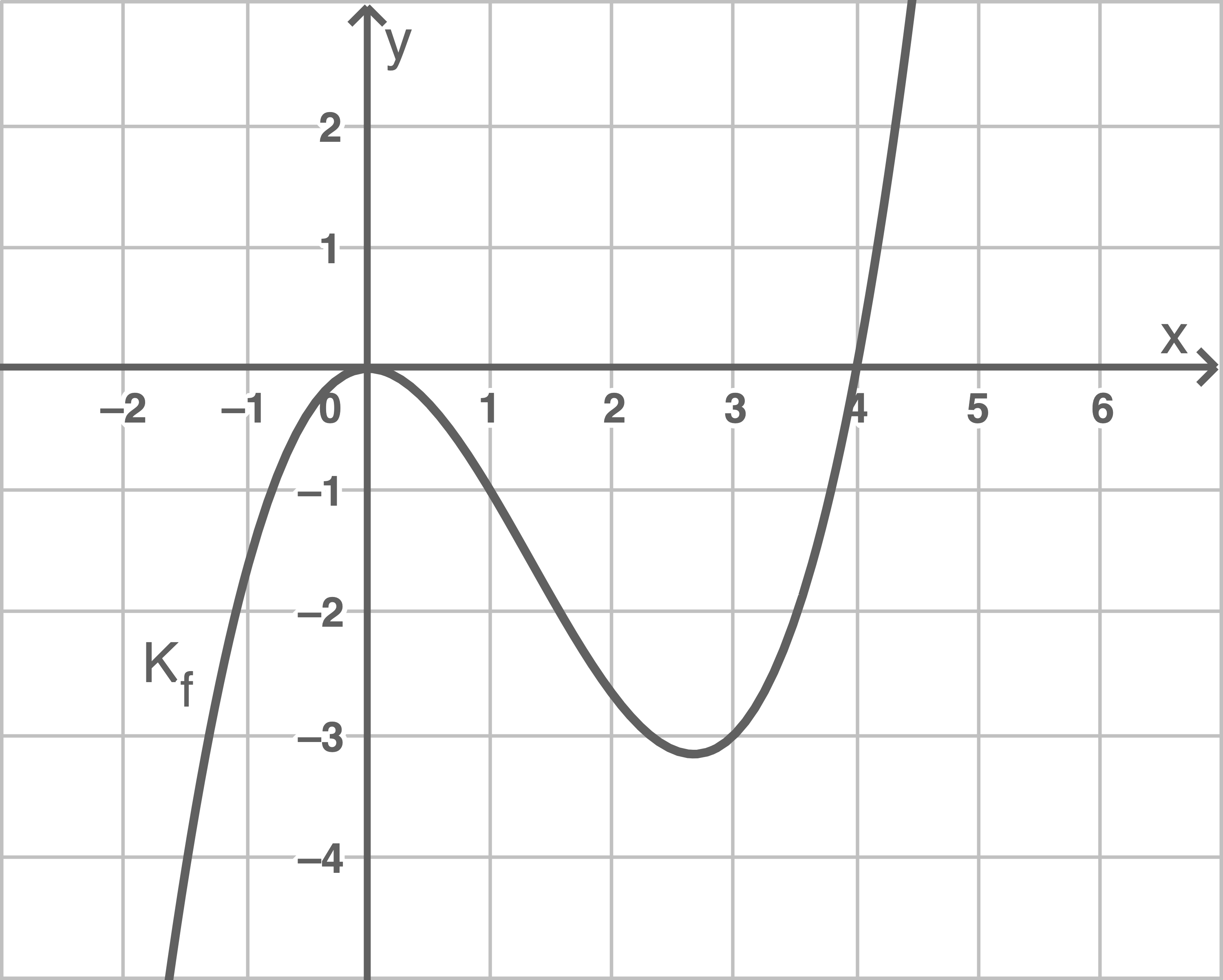
a)
Ermittle den Wert von 
Im Folgenden gilt
(2 BE)
b)
Berechne die Koordinaten des Tiefpunktes von 
(4 BE)
c)
Berechne die Größe des Winkels, unter dem die Wendeltangente  an
an  die
die  -Achse schneidet.
-Achse schneidet.
(5 BE)
d)
Der Graph der in  definierten Funktion
definierten Funktion  geht aus
geht aus  durch Verschiebung um
durch Verschiebung um  in negative
in negative  -Richtung sowie eine Verschiebung in
-Richtung sowie eine Verschiebung in  -Richtung hervor.
-Richtung hervor.
Es gilt
Zeige unter Verwendung der Funktionsgleichung von dass der Graph von
dass der Graph von  an der Stelle
an der Stelle  rechtsgekrümmt ist.
rechtsgekrümmt ist.
Es gilt
Zeige unter Verwendung der Funktionsgleichung von
(3 BE)
e)
Der Ursprung, der Punkt  und der Punkt
und der Punkt  bilden für
bilden für  im 4. Quadranten ein Dreieck mit dem Flächeninhalt
im 4. Quadranten ein Dreieck mit dem Flächeninhalt 
Erläutere die Bedeutung der Stelle die mit folgender Rechnung ermittelt wird:
die mit folgender Rechnung ermittelt wird:
 Dabei gilt:
Dabei gilt:
 und
und  und
und 
Erläutere die Bedeutung der Stelle
(3 BE)
f)
Eine quadratische Funktion  hat dieselben Nullstellen wie
hat dieselben Nullstellen wie  . Die Graphen von
. Die Graphen von  und
und  schließen im 4. Quadranten zwei gleich große Flächenstücke ein.
schließen im 4. Quadranten zwei gleich große Flächenstücke ein.
Ermittle eine Gleichung von
Ermittle eine Gleichung von
(4 BE)
Aufgabe I 2.2
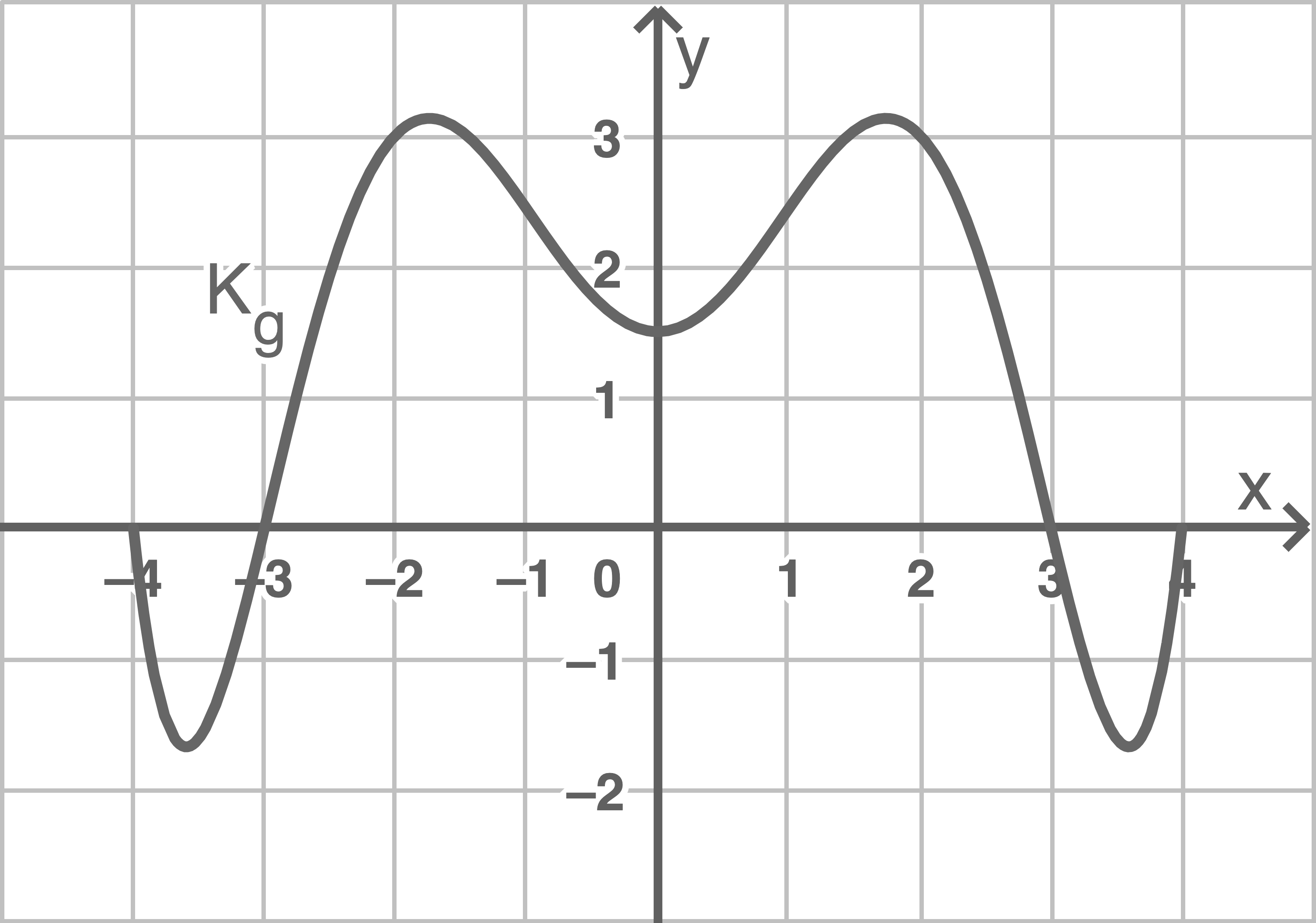
Die Abbildung zeigt den GraphenEntscheide, ob die folgenden Aussagen wahr oder falsch sind.
Begründe jeweils deine Entscheidung.
(1)
Die zugehörige Ableitungsfunktion  hat genau 5 Nullstellen.
hat genau 5 Nullstellen.
(2)
Es gilt: 
(3)
Jede Stammfunktion von  ist für
ist für  monoton wachsend.
monoton wachsend.
(6 BE)
Aufgabe I 2.3
Die inHierbei ist
a)
Zeichne den Graphen von  für
für 
(3 BE)
b)
Gib anhand der Zeichnung näherungsweise den Zeitpunkt an, zu welchem die Konzentration am stärksten abnimmt.
(1 BE)
c)
Es gilt  und
und  Erläutere die Bedeutung dieser beiden Aussagen hinsichtlich des Verlaufs des Graphen von
Erläutere die Bedeutung dieser beiden Aussagen hinsichtlich des Verlaufs des Graphen von 
Interpretiere diese beiden Aussagen im Sachzusammenhang.
Interpretiere diese beiden Aussagen im Sachzusammenhang.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung I 1.1
a)
b)
Die Tangente an  ist waagerecht, wenn gilt:
ist waagerecht, wenn gilt:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/771325593db0fa935320b87063e45209dcc66ab52c592529e154ece68c96f42d?color=5a5a5a) Mit dem Satz vom Nullprodukt folgt
Mit dem Satz vom Nullprodukt folgt  und
und  Zweite Ableitung bestimmen:
Zweite Ableitung bestimmen:
 Es gilt also:
Es gilt also:
 Folglich liegt an der Stelle
Folglich liegt an der Stelle  ein Sattelpunkt vor.
ein Sattelpunkt vor.
 An der Stelle
An der Stelle  liegt also ein Tiefpunkt vor.
liegt also ein Tiefpunkt vor.
c)
d)
Tangentengleichung  bestimmen
Die allgemeine Tangentengleichung ist von der Form
bestimmen
Die allgemeine Tangentengleichung ist von der Form  Für die Tangente
Für die Tangente  durch den Punkt
durch den Punkt  gilt:
gilt:
![\(\begin{array}[t]{rll}
m&=& f](https://mathjax.schullv.de/debe19eff287ef9d48115f3cfce88ae59c581c586fc083d803f0891b01fc0103?color=5a5a5a) Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  in die allgemeine Tangentengleichung liefert:
in die allgemeine Tangentengleichung liefert:
![\(\begin{array}[t]{rll}
0&=& -\dfrac{4}{3}\cdot 2+c \quad \scriptsize \mid\; +\dfrac{8}{3}\\[5pt]
\dfrac{8}{3}&=& c
\end{array}\)](https://mathjax.schullv.de/11cd9da3bfa6512c7cf5232f6e058db5f0f77cd77af3b0660255c7ee0008be30?color=5a5a5a) Daraus folgt
Daraus folgt  Tangentengleichung
Tangentengleichung  bestimmen
Für die Tangente
bestimmen
Für die Tangente  durch den Punkt
durch den Punkt  gilt:
gilt:

 Daraus folgt
Daraus folgt  Schnittstelle der beiden Wendetangenten berechnen:
Schnittstelle der beiden Wendetangenten berechnen:
![\(\begin{array}[t]{rll}
-\dfrac{4}{3}x+\dfrac{8}{3}&=& \dfrac{4}{3} &\quad \scriptsize \; \bigg \vert\, \;-\dfrac{8}{3} \\[5pt]
-\dfrac{4}{3}x&=& -\dfrac{4}{3} &\quad \scriptsize \; \bigg \vert\,\; :\left(-\dfrac{4}{3}\right) \\[5pt]
x&=& 1
\end{array}\)](https://mathjax.schullv.de/7756fafb0309d5434f8e42d1eba0c6ed6abea2444d0da412546c09f7b9eb91ce?color=5a5a5a) Wegen
Wegen  folgen die Koordinaten des Schnittpunktes
folgen die Koordinaten des Schnittpunktes 
e)
Durch Einzeichnen des Dreiecks in die Abbildung des Graphen  aus Aufgabenteil a) lässt sich schließen, dass sich der Flächeninhalt aus der Differenz der Tangente im jeweiligen Abschnitt und der Funktion
aus Aufgabenteil a) lässt sich schließen, dass sich der Flächeninhalt aus der Differenz der Tangente im jeweiligen Abschnitt und der Funktion  zusammensetzt.
zusammensetzt.
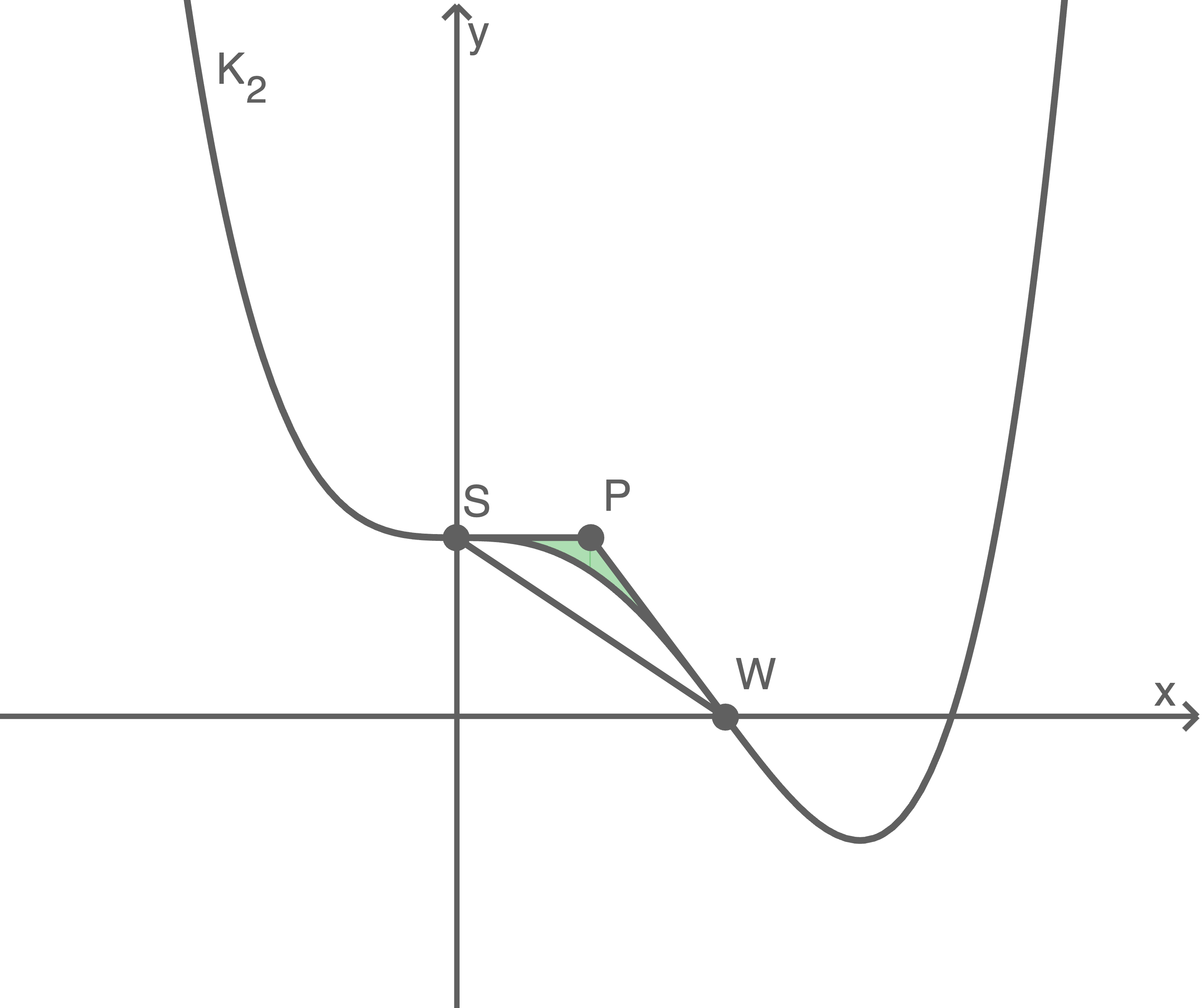 Für den Inhalt der Fläche, welche von
Für den Inhalt der Fläche, welche von  und
und  zwischen den Punkten
zwischen den Punkten  und
und  eingeschlossen wird, gilt:
eingeschlossen wird, gilt:
![\(\begin{array}[t]{rll}
A_{SP}&=& \,\bigg \vert \,\displaystyle\int_{0}^{1}t_S(x)-f(x)\;\mathrm dx\,\bigg \vert \,&\\[5pt]
&=& \,\bigg \vert \,\displaystyle\int_{0}^{1}-\dfrac{1}{12}x^4+\dfrac{1}{3}x^3\;\mathrm dx\,\bigg \vert \,& \\[5pt]
&=& \,\bigg \vert \,\left[-\dfrac{1}{60}x^5+\dfrac{1}{12}x^4\right]_0^1\,\bigg \vert \,& \\[5pt]
&=& \,\bigg \vert \,-\dfrac{1}{60}+\dfrac{1}{12}\,\bigg \vert \,& \\[5pt]
&=& \dfrac{1}{15} \; [\text{FE}]
\end{array}\)](https://mathjax.schullv.de/3aee803df13ab17aee6cb35bf0e3cfb0e2200189fc2c795bd6ad0714611679eb?color=5a5a5a) Für den Inhalt der Fläche, welche von
Für den Inhalt der Fläche, welche von  und
und  zwischen den Punkten
zwischen den Punkten  und
und  eingeschlossen wird, gilt:
eingeschlossen wird, gilt:
![\(\begin{array}[t]{rll}
A_{PW}&=& \,\bigg \vert \,\displaystyle\int_{1}^{2}t_W(x)-f(x)\;\mathrm dx\,\bigg \vert \,& \\[5pt]
&=& \,\bigg \vert \,\displaystyle\int_{1}^{2}-\dfrac{1}{12}x^4+\dfrac{1}{3}x^3-\dfrac{4}{3}x+\dfrac{4}{3}\;\mathrm dx\,\bigg \vert \,& \\[5pt]
&=& \,\bigg \vert \,\left[-\dfrac{1}{60}x^5+\dfrac{1}{12}x^4-\dfrac{4}{6}x^2+\dfrac{4}{3}x\right]_1^2\,\bigg \vert \,& \\[5pt]
&=& \,\bigg \vert \,\left(-\dfrac{1}{60}\cdot 32+\dfrac{1}{12}\cdot 16-\dfrac{4}{6}\cdot 4+\dfrac{4}{3}\cdot 2- \left(-\dfrac{1}{60}+\dfrac{1}{12}-\dfrac{4}{6}+\dfrac{4}{3}\right)\right)\,\bigg \vert \,& \\[5pt]
&=& \dfrac{1}{15} \; [\text{FE}]
\end{array}\)](https://mathjax.schullv.de/0020e87e6f178442a56decdf27ec1b133036aeb402fc40b07d837ae5cb3cc552?color=5a5a5a) Der gesamte Flächeninhalt der Teilfläche oberhalb von
Der gesamte Flächeninhalt der Teilfläche oberhalb von  ergibt sich also zu:
ergibt sich also zu:
![\(\begin{array}[t]{rll}
A&=& A_{SP} + A_{PW} & \\[5pt]
&=& \dfrac{2}{15} \; [\text{FE}]
\end{array}\)](https://mathjax.schullv.de/fdcb4407b37d65d6ce3bdc3cb886cbab018aedfe73a06c79c3fc8f93aa382986?color=5a5a5a)

Lösung I 1.2
a)
b)
Die  -Konzentration wird über die Jahre gemessen und weist einen stetigen Anstieg auf. Um ein mathematisches Modell für diesen Verlauf zu erstellen, bietet sich eine Exponentialfunktion an, da der Anstieg über die Zeit exponentiell zu sein scheint.
Für eine Exponentialfunktion der Form
-Konzentration wird über die Jahre gemessen und weist einen stetigen Anstieg auf. Um ein mathematisches Modell für diesen Verlauf zu erstellen, bietet sich eine Exponentialfunktion an, da der Anstieg über die Zeit exponentiell zu sein scheint.
Für eine Exponentialfunktion der Form  wobei
wobei  die
die  -Konzentration im Jahr 2012,
-Konzentration im Jahr 2012,  die Wachstumsrate und
die Wachstumsrate und  das Jahr 2012 ist, kann die Funktionsgleichung durch Einsetzen des Wertepaars
das Jahr 2012 ist, kann die Funktionsgleichung durch Einsetzen des Wertepaars  bestimmt werden:
Insgesamt ergibt sich
bestimmt werden:
Insgesamt ergibt sich 
c)
d)
Da das Modell nur auf einem kleinen Datenbereich beruht, ist es unsicher, dieses auf Zeiträume von fast 100 Jahren (bis 2100) zu übertragen. Es kann zu unvorhersehbaren Ereignissen kommen, wie zum Beispiel:
- Veränderung der weltweiten Emissionspolitik
- Technologischer Fortschritt in
-Reduktion
- Änderungen im natürlichen
-Kreislauf (z.B. durch Vulkanausbrüche, Veränderungen in der Vegetation)
Lösung I 2.1
a)
Aus der Abbildung kann abgelesen werden, dass der Punkt  auf
auf  liegt. Einsetzen der Koordinaten in die Funktionsgleichung von
liegt. Einsetzen der Koordinaten in die Funktionsgleichung von  liefert:
liefert:
![\(\begin{array}[t]{rll}
-3&=& a\cdot 3^2\cdot (3-4) \\[5pt]
-3&=& -9a \quad \scriptsize \mid\; :(-9) \\[5pt]
\dfrac{1}{3}&=& a
\end{array}\)](https://mathjax.schullv.de/b5dca5cd08289172bc96e40c9f7a16b77d775fa4f37c8137c0153064fda63f62?color=5a5a5a)
b)
Ableitung bestimmen:
![\(\begin{array}[t]{rll}
f(x)&=& \dfrac{1}{3}x^2\cdot (x-4)& \\[5pt]
&=&\dfrac{1}{3}x^3-\dfrac{4}{3}x^2
\end{array}\)](https://mathjax.schullv.de/b6088e54c2bd7b2f76018e45abb59daf7f682b2659cd1b7df51f554c52d60f65?color=5a5a5a)
 Notwendige Bedingung für Extremstellen anwenden:
Notwendige Bedingung für Extremstellen anwenden:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/646db064de7ca821aa984678064379524173c4bdd11f290a4f28e7c8066930ea?color=5a5a5a) Mit dem Satz vom Nullprodukt folgt
Mit dem Satz vom Nullprodukt folgt  und
und  Der Abbildung kann entnommen werden, dass sich der Tiefpunkt an der Stelle
Der Abbildung kann entnommen werden, dass sich der Tiefpunkt an der Stelle  befindet.
befindet.
 Der Tiefpunkt hat folglich die Koordinaten
Der Tiefpunkt hat folglich die Koordinaten 
c)
1. Schritt: Wendestelle berechnen
Ableitung bestimmen:
 Notwendige Bedingung für Wendestellen anwenden:
Notwendige Bedingung für Wendestellen anwenden:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/bcd113d3808e5744d3d88ed1f6ae6c74542be6bb57a21b52a10bac6e6b13a301?color=5a5a5a) Steigung von
Steigung von  berechnen
Für die Steigung
berechnen
Für die Steigung  der Wendetangente ergibt sich:
der Wendetangente ergibt sich:
 Winkel bestimmen
Für den Winkel zwischen der Wendetangente und der
Winkel bestimmen
Für den Winkel zwischen der Wendetangente und der  -Achse folgt:
-Achse folgt:
![\(\begin{array}[t]{rll}
\tan(\theta)&=& m &\quad \scriptsize \mid\; \arctan \\[5pt]
\theta&=& \arctan\left(\dfrac{4}{3}\right) \\[5pt]
\theta&\approx& 53,13^\circ
\end{array}\)](https://mathjax.schullv.de/a6b065110bddae0b4b4c73b4262b953358cbcc311f35832307ea0c754a68d183?color=5a5a5a)
d)
Ableitungen bestimmen:


 Der Graph von
Der Graph von  geht aus dem Graphen der Funktion
geht aus dem Graphen der Funktion  durch Verschiebung um
durch Verschiebung um  in positive
in positive  -Richtung hervor. Die Verschiebung entlang der
-Richtung hervor. Die Verschiebung entlang der  -Achse ist für die Krümmung der Funktion
-Achse ist für die Krümmung der Funktion  irrelevant. Es gilt:
irrelevant. Es gilt:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/d9f9adebcc82ef2ef173903870d317aff26f39eee75db9207bb06d778443c308?color=5a5a5a) Daher ist der Graph von
Daher ist der Graph von  an der Stelle
an der Stelle  rechtsgekrümmt.
rechtsgekrümmt.
e)
f)
Mit dem Satz vom Nullprodukt folgt direkt, dass  die Nullstellen
die Nullstellen  und
und  hat.
Eine quadratische Funktion, die dieselben Nullstellen wie
hat.
Eine quadratische Funktion, die dieselben Nullstellen wie  hat, kann in der folgenden Form geschrieben werden:
hat, kann in der folgenden Form geschrieben werden:
![\(\begin{array}[t]{rll}
p(x)&=&k \cdot x \cdot(x-4) & \\[5pt]
&=&k\cdot (x^2-4x)
\end{array}\)](https://mathjax.schullv.de/3b6d8ac7bf5fbf9a0a7fa50dbc1e2b6a2188d4fbaa1dbb07ab7162772cf7c78d?color=5a5a5a) Die Graphen von
Die Graphen von  und
und  schließen im 4. Quadranten zwei gleich große Flächenstücke ein. Es muss also gelten:
Die gesuchte Funktionsgleichung ist also gegeben durch
schließen im 4. Quadranten zwei gleich große Flächenstücke ein. Es muss also gelten:
Die gesuchte Funktionsgleichung ist also gegeben durch 
Lösung I 2.2
(1)
Die Aussage ist wahr.
Die 5 Extremstellen von  entsprechen 5 Nullstellen von
entsprechen 5 Nullstellen von 
(2)
Die Aussage ist wahr.
Der Flächeninhalt oberhalb der  -Achse ist im betrachteten Intervall größer als unterhalb der
-Achse ist im betrachteten Intervall größer als unterhalb der  -Achse. Damit ist das Integral insgesamt positiv.
-Achse. Damit ist das Integral insgesamt positiv.
(3)
Die Aussage ist falsch.
Die Funktion  verläuft im betrachteten Intervall auch unterhalb der
verläuft im betrachteten Intervall auch unterhalb der  -Achse. Da
-Achse. Da  als Ableitung jeder Stammfunktion von
als Ableitung jeder Stammfunktion von  die Steigung dieser angibt, sind die Stammfunktionen in diesem Bereich nicht monoton wachsend.
die Steigung dieser angibt, sind die Stammfunktionen in diesem Bereich nicht monoton wachsend.
Lösung I 2.3
a)
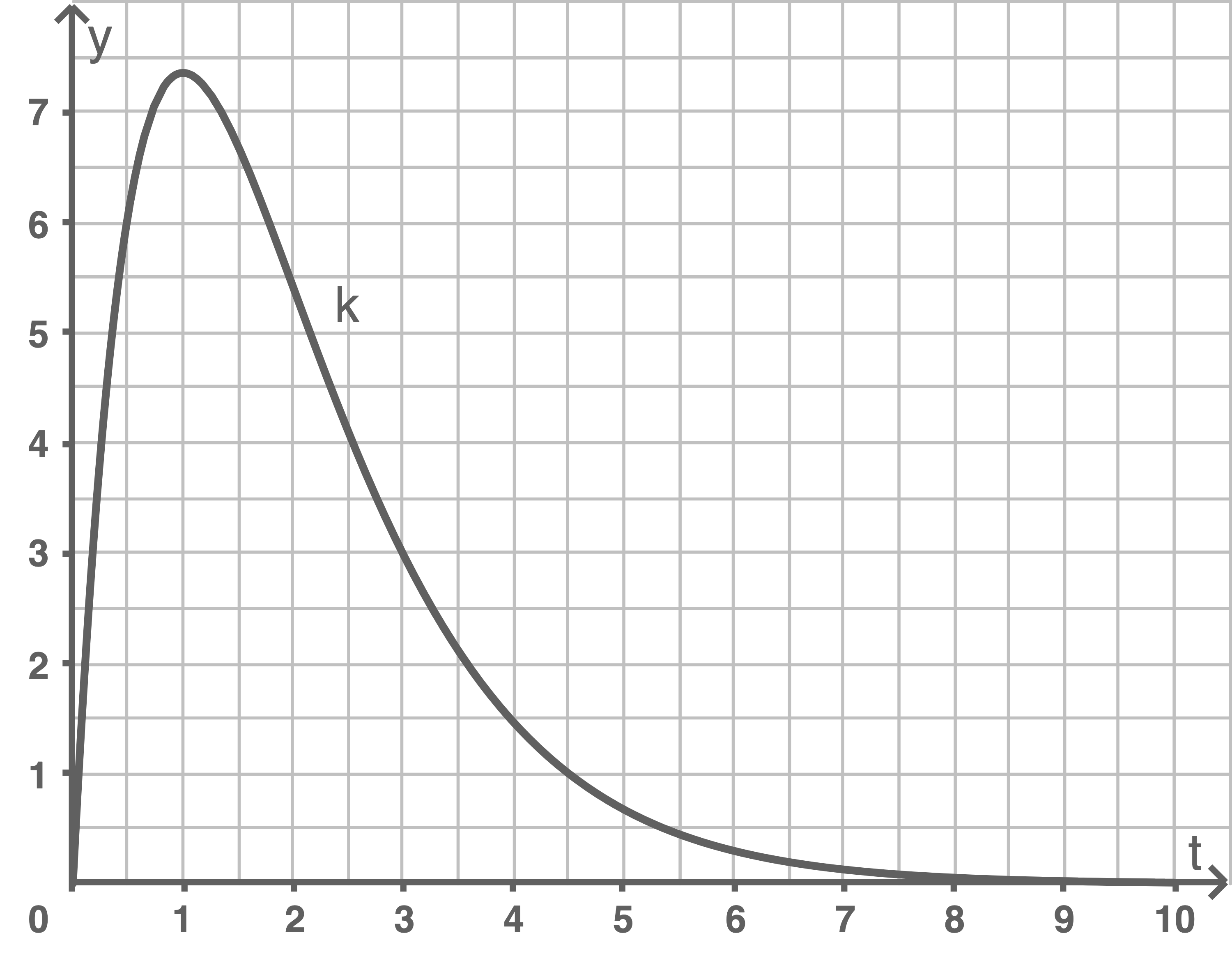
b)
Aus der Abbildung lässt sich die Wendestelle bei  ablesen.
ablesen.
c)
Bedeutung der Aussagen erläutern
 : Die erste Ableitung ist negativ, was bedeutet, dass die Konzentration des Medikaments bei
: Die erste Ableitung ist negativ, was bedeutet, dass die Konzentration des Medikaments bei  abnimmt. Das Medikament wird also zu diesem Zeitpunkt weiter abgebaut.
abnimmt. Das Medikament wird also zu diesem Zeitpunkt weiter abgebaut.
 : Die zweite Ableitung ist positiv, was darauf hinweist, dass die Abnahme der Konzentration langsamer wird.
Interpretation im Sachzusammenhang
Bei
: Die zweite Ableitung ist positiv, was darauf hinweist, dass die Abnahme der Konzentration langsamer wird.
Interpretation im Sachzusammenhang
Bei  nimmt die Konzentration des Medikaments zwar weiterhin ab, aber langsamer. Dies könnte darauf hindeuten, dass sich die Konzentration demnächst stabilisieren wird.
nimmt die Konzentration des Medikaments zwar weiterhin ab, aber langsamer. Dies könnte darauf hindeuten, dass sich die Konzentration demnächst stabilisieren wird.