Anwendungsorientierte Analysis 2
3
Ein Gezeitenkraftwerk nutzt die Energie aus der Bewegung des Wassers bei Ebbe und Flut zur Stromerzeugung. Die Funktion 
mit
![\(t \in[0 ; 12]\)](https://www.schullv.de/resources/formulas/e85fc803868eb35bba4c2fa676273c509a23686ffdfb5892853dd5e5079d868c_light.svg)
modelliert die momentane Änderungsrate des Wasservolumens im Rückhaltebecken eines Gezeitenkraftwerkes über einen Zeitraum von 12 Stunden.
Hierbei ist
die Zeit seit Beobachtungsbeginn 
in Stunden.
wird in Kubikmeter pro Stunde 
angegeben.
Bei Flut fließt das Wasser in das Rückhaltebecken und ist positiv.
Bei Ebbe fließt das Wasser aus dem Rückhaltebecken und ist negativ.
mit
modelliert die momentane Änderungsrate des Wasservolumens im Rückhaltebecken eines Gezeitenkraftwerkes über einen Zeitraum von 12 Stunden.
Hierbei ist
die Zeit seit Beobachtungsbeginn in Stunden.
wird in Kubikmeter pro Stunde angegeben.
Bei Flut fließt das Wasser in das Rückhaltebecken und
ist positiv.
Bei Ebbe fließt das Wasser aus dem Rückhaltebecken und
ist negativ.
3.1
Skizziere das Schaubild von 
Gib den Zeitraum der Flut an.
Gib den Zeitraum der Flut an.
3
3.2
Bestimme, wie viele Liter Wasser pro Minute maximal aus dem Rückhaltebecken abfließen.
Ein Liter entspricht einem Kubikdezimeter.
Ein Liter entspricht einem Kubikdezimeter.
2
3.3
Beziehe Stellung zu folgender Aussage:
„Es gibt einen vierstündigen Zeitraum, in dem der Wasserzufluss den Wert von 
nie unterschreitet.“
nie unterschreitet.“
2
3.4
Vier Stunden nach Beobachtungsbeginn befinden sich 
Wasser im Rückhaltebecken.
Ermittle, zu welchem Zeitpunkt dieser Wasserstand das nächste Mal erreicht wird.
Begründe, dass das Rückhaltebecken mehr als
Wasser fassen muss.
Wasser im Rückhaltebecken.
Ermittle, zu welchem Zeitpunkt dieser Wasserstand das nächste Mal erreicht wird.
Begründe, dass das Rückhaltebecken mehr als
Wasser fassen muss.
3
10
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
3.1
positiv. Also ist im Zeitraum von 0 bis 6 Stunden nach Beobachtungsbeginn Flut.
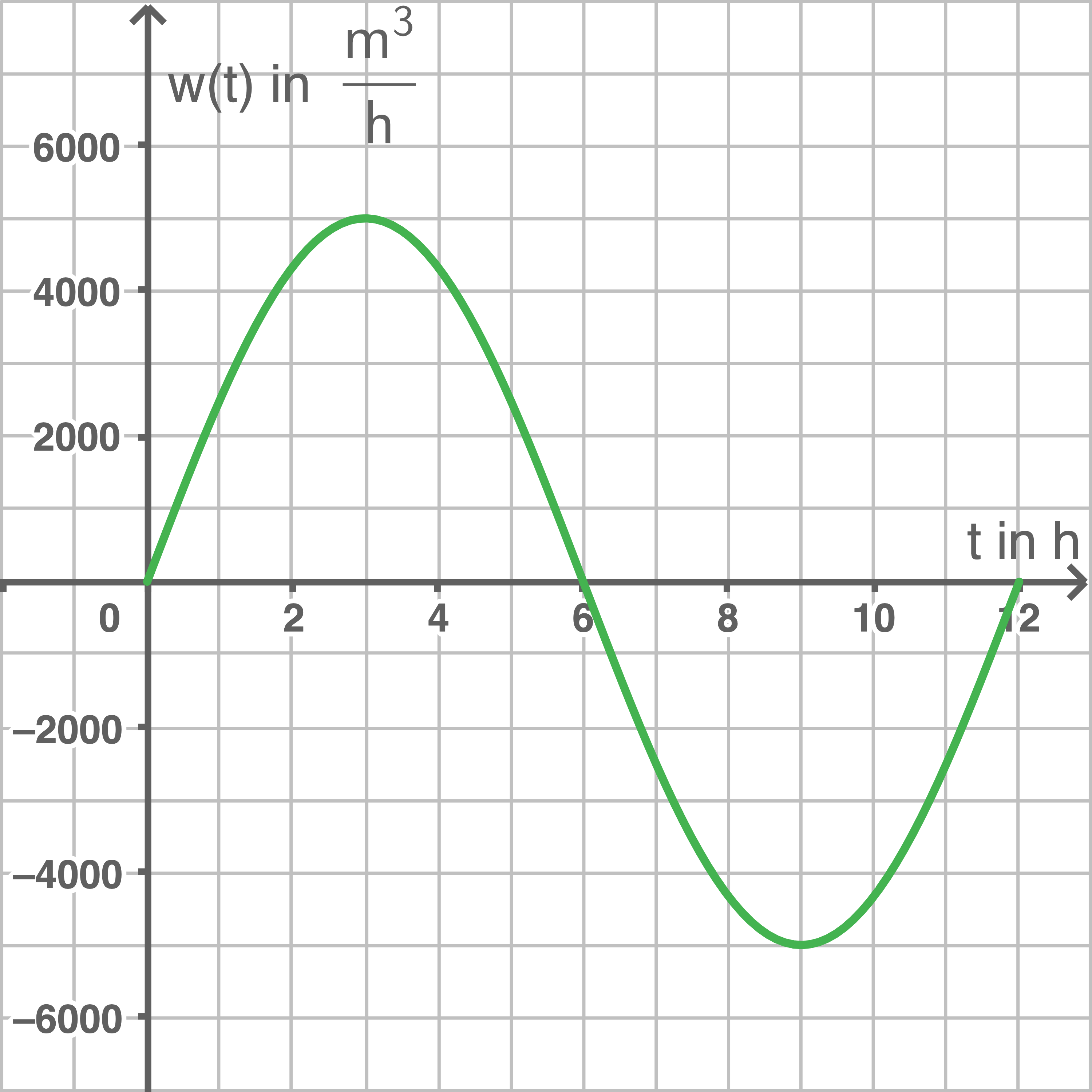
3.2
Gesucht ist das Minimum von Da es sich bei um eine gestreckte Sinusfunktion handelt, lassen sich die Maximal- und Minimalwerte von anhand der Amplitude bestimmen.
Die Amplitude beträgt 
Es fließen also maximal 
aus dem Rückhaltebecken ab.
Es fließen also maximal ca. 83.333 Liter pro Minute aus dem Rückhaltebecken.
Da es sich bei um eine gestreckte Sinusfunktion handelt, lassen sich die Maximal- und Minimalwerte von anhand der Amplitude bestimmen.
Die Amplitude beträgt Es fließen also maximal aus dem Rückhaltebecken ab.
Es fließen also maximal ca. 83.333 Liter pro Minute aus dem Rückhaltebecken.
3.3
ergänzt, lassen sich die Schnittstellen 
und 
ablesen.
In diesem Intervall ![\([1;5]\)](https://www.schullv.de/resources/formulas/537aa42c72cde4f110c2f0ebdd6274a8c61a3e51c25142ee85d6d83a6bae297c_light.svg)
verläuft der Graph von an keiner Stelle unterhalb der Geraden, sodass in diesem Intervall die Zuflussrate von 
nicht unterschritten wird.
Dieses Intervall hat ungefähr die Länge 
sodass die Aussage zutrifft.
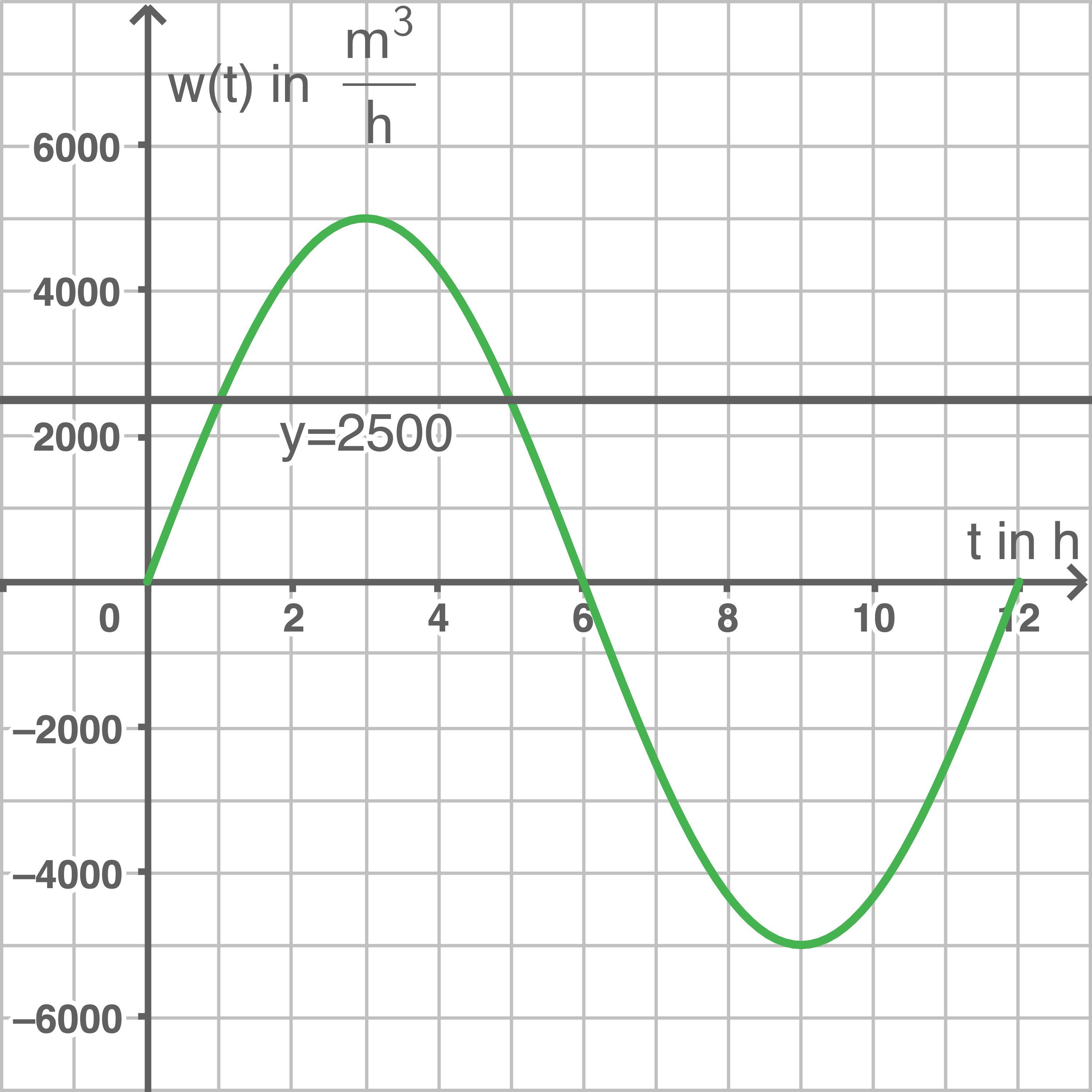
3.4
Nächsten Zeitpunkt ermitteln
besitzt die Periode 
Innerhalb von 12 Stunden fließt also genauso viel Wasser in das Rückhaltebecken, wie abfließt. Der Wasserstand von 
wird also das nächste Mal 
Stunden nach Beobachtungsbeginn erreicht.
Fassungsvermögen begründen
Vier Stunden nach Beobachtungsbeginn befinden sich bereits Wasser im Rückhaltebecken. Aufgrund der Periode von 12 Stunden, fließen noch weitere 2 Stunden lang Wasser in das Becken. Dies lässt sich auch dem Schaubild entnehmen.
Die Menge des Wassers, das in dieser Zeit noch hinzufließt, lässt sich mit Hilfe eines Integrals berechnen:
Wenn bereits Wasser im Rückhaltebecken sind, fließen noch weitere 
hinein. Es muss also mehr als 
Wasser fassen können.
besitzt die Periode Innerhalb von 12 Stunden fließt also genauso viel Wasser in das Rückhaltebecken, wie abfließt. Der Wasserstand von wird also das nächste Mal Stunden nach Beobachtungsbeginn erreicht.
Fassungsvermögen begründen
Vier Stunden nach Beobachtungsbeginn befinden sich bereits Wasser im Rückhaltebecken. Aufgrund der Periode von 12 Stunden, fließen noch weitere 2 Stunden lang Wasser in das Becken. Dies lässt sich auch dem Schaubild entnehmen.
Die Menge des Wassers, das in dieser Zeit noch hinzufließt, lässt sich mit Hilfe eines Integrals berechnen:
Wenn bereits ![\( \displaystyle\int_{4}^{6}w(t)\;\mathrm dt \approx 4775\,[\text{m}^3]\)](https://www.schullv.de/resources/formulas/0d4128c4751a9fe404170b2bd8a93d14259cfffb5be93b53e759160a80005305_light.svg)
![\(\begin{array}[t]{rll}
& \displaystyle\int_{4}^{6}w(t)\;\mathrm dt \\[5pt]
=& \displaystyle\int_{4}^{6}5000\cdot \sin\left(\dfrac{\pi}{6}t\right)\;\mathrm dt \\[5pt]
=& 5000 \cdot \left[-\dfrac{6}{\pi}\cos\left(\dfrac{\pi}{6}t\right)\right]_4^6 \\[5pt]
=& -5000\cdot \left(\dfrac{6}{\pi}\cos\left(\dfrac{\pi}{6}\cdot 6\right) - \dfrac{6}{\pi}\cos\left(\dfrac{\pi}{6}\cdot 4\right) \right)&\quad \scriptsize \mid\; \\[5pt]
=& -5000\cdot \dfrac{6}{\pi}\cdot \left(\cos\left(\pi\right) - \cos\left(\dfrac{2}{3}\pi\right) \right) \\[5pt]
=& -5000\cdot \dfrac{6}{\pi}\cdot \left(-1 - (-0,5) \right) \\[5pt]
=& \dfrac{15000}{\pi}\\[5pt]
\approx& 4775\,[\text{m}^3]
\end{array}\)](https://www.schullv.de/resources/formulas/56b8bd9b2496f7cd1fc2cea0785afd9fed5a487139173a196ff5477778415499_light.svg)
Wasser im Rückhaltebecken sind, fließen noch weitere hinein. Es muss also mehr als Wasser fassen können.