Wahlaufgaben
4 Analysis
Gegeben ist eine im IntervallDer Graph von
Der Wertebereich von
a)
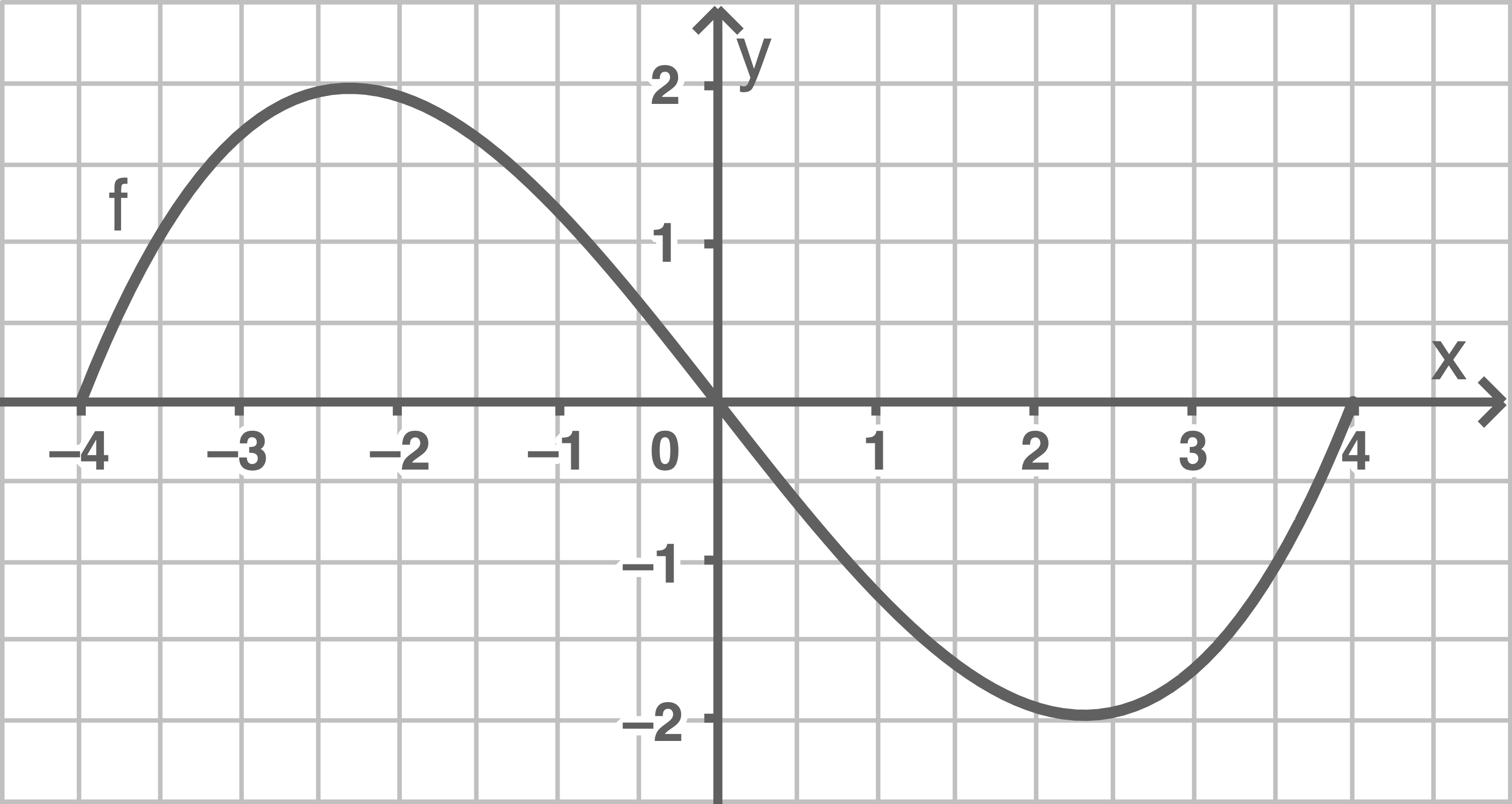
Skizziere den Graphen der Funktion  , wenn bekannt ist, dass
, wenn bekannt ist, dass  gilt.
gilt.
(3 BE)
b)
Bestimme eine Funktionsgleichung einer trigonometrischen Funktion  , sodass
, sodass  und
und  im Intervall
im Intervall ![\([-4; 4]\)](https://mathjax.schullv.de/45030092f707f37f6d181387a8976f993fc2ab4591e710ff193d5590d81f3fa3?color=5a5a5a) dieselben Nullstellen haben.
dieselben Nullstellen haben.
(2 BE)
4 Lineare Algebra
Der Punkt
a)
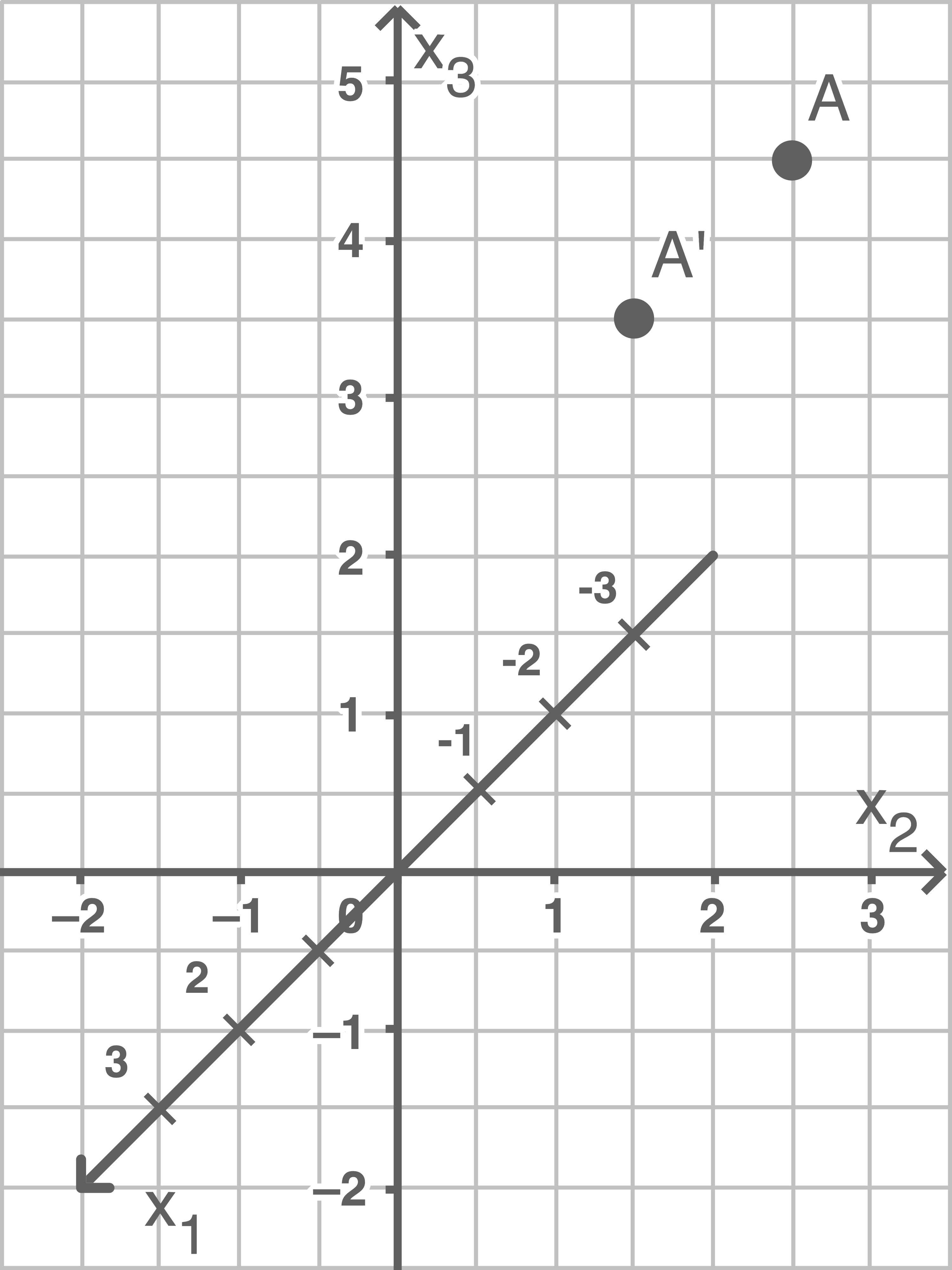
Zeichne  und
und  in ein geeignetes Koordinatensystem ein.
in ein geeignetes Koordinatensystem ein.
(2 BE)
b)
(3 BE)
5 Analysis
Die Abbildung zeigt den Graphen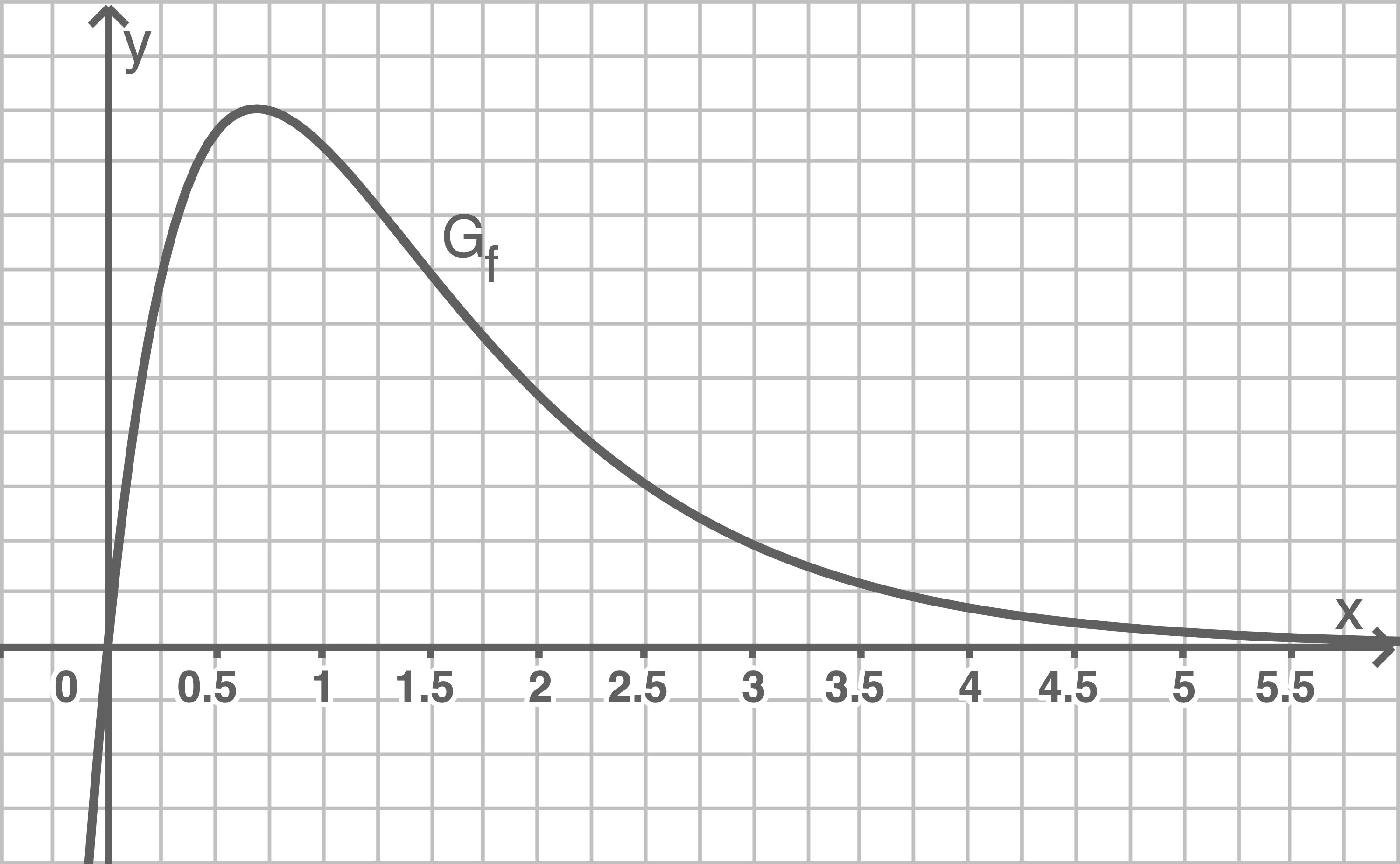
a)
Weise rechnerisch nach, dass  die einzige Nullstelle von
die einzige Nullstelle von  ist.
ist.
(2 BE)
b)
Entscheide mit Hilfe der Abbildung, ob die folgenden Aussagen wahr oder falsch sind. Begründe jeweils deine Entscheidung.
(1)  (2)
(2) 
(3 BE)
5 Lineare Algebra
Gegeben ist die Gerade
a)
Weise nach, dass  dem Abstand von
dem Abstand von  zur Geraden
zur Geraden  entspricht.
entspricht.
(2 BE)
b)
Bestimme die Koordinaten eines Punktes  auf
auf  , der zusammen mit
, der zusammen mit  und
und  ein gleichschenkliges Dreieck bildet.
ein gleichschenkliges Dreieck bildet.
(3 BE)
6 Stochastik
(PLA; mit Hilfsmitteln) Bearbeite die folgende Aufgabe unter Berücksichtigung der einzelnen Problemlöseschritte. Dokumentiere und reflektiere deine Vorgehensweise. Eine Klasse will ein Glücksspiel in Form eines Zufallsexperiments anbieten, bei dem sie im langfristigen Mittel 1 € Gewinn pro Spiel macht. Entwerfe und beschreibe ein dazu passendes mehrstufiges Zufallsexperiment.
(10 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?4 Analysis
a)
b)
Die drei am nächsten zum Ursprung gelegenen Nullstellen der Funktion  sind bei
sind bei  und
und  Durch Streckung in
Durch Streckung in  -Richtung mit dem Faktor
-Richtung mit dem Faktor  nimmt die Sinusfunktion somit dieselben Nullstellen wie
nimmt die Sinusfunktion somit dieselben Nullstellen wie  an. Eine mögliche Funktionsgleichung einer trigonometrischen Funktion mit denselben Nullstellen wie
an. Eine mögliche Funktionsgleichung einer trigonometrischen Funktion mit denselben Nullstellen wie  lautet deshalb
lautet deshalb 
4 Lineare Algebra
a)
b)
Da  und
und  symmetrisch zur
symmetrisch zur  -Ebene liegen und
-Ebene liegen und  auf der
auf der  -Achse, d.h. innerhalb der
-Achse, d.h. innerhalb der  -Ebene, liegt, ist
-Ebene, liegt, ist  von beiden Punkten gleich weit entfernt.
von beiden Punkten gleich weit entfernt.
5 Analysis
a)
b)
(1)
Die Aussage ist falsch.
Der Graph ist an der Stelle  rechtsgekrümmt, weshalb
rechtsgekrümmt, weshalb  gelten muss.
gelten muss.
(2)
Die Aussage ist wahr.
Es gilt  Da die Funktion
Da die Funktion  im gegebenen Intervall jedoch einen kleineren Flächeninhalt einschließt als die Funktion
im gegebenen Intervall jedoch einen kleineren Flächeninhalt einschließt als die Funktion  gilt die angegebene Ungleichung.
gilt die angegebene Ungleichung.
5 Lineare Algebra
a)
b)
6 Stochastik
Grundkonzept Ein mögliches Glücksspiel könnte eine mehrstufige Münzwurf- oder Würfelsequenz mit Einsatz sein, bei der Spieler entweder Geld gewinnen oder ihren Einsatz verlieren. Die Wahrscheinlichkeit des Gewinns und der Verlusthöhe sollten so eingestellt werden, dass der Erwartungswert- Einsatz: Der Spieler zahlt
Einsatz, um am Spiel teilzunehmen.
- Erste Stufe: Der Spieler würfelt mit einem fairen sechsseitigen Würfel.
- Zweite Stufe: Der Spieler würfelt ein zweites Mal mit demselben Würfel.
- Gewinnbedingung: Wenn bei beiden Würfen dieselbe Zahl geworfen wird, erhält der Spieler
Ansonsten erhält er nichts.