Stochastik 1
1
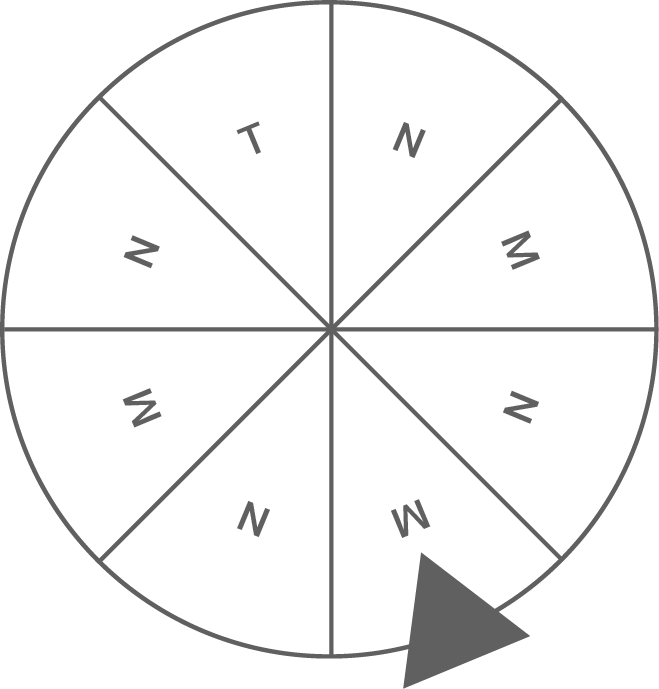
Bei der Eröffnungsfeier einer Wakeboard-Anlage bietet der Veranstalter ein Glücksspiel an. Das abgebildete Glücksrad besteht aus acht gleich großen Sektoren. Wenn das Rad nach einer Drehung zum Stillstand kommt, zeigt der Pfeil genau auf einen Sektor.
Jeder Besucher darf das Glücksrad genau einmal drehen. Dabei kann er eine Testfahrt auf der neuen Wakeboard-Anlage (T) oder das Maskottchen des Betreibers (M) gewinnen. Andernfalls gewinnt er nichts (N).
1.1
Drei Besucher drehen nacheinander das Glücksrad. Berechne jeweils die Wahrscheinlichkeit für die folgenden Ereignisse:
A: Alle drei Besucher gewinnen eine Testfahrt.
B: Genau einer der Besucher gewinnt eine Testfahrt.
B: Genau einer der Besucher gewinnt eine Testfahrt.
3
1.2
Ein Besucher dreht das Glücksrad und gewinnt.
Bestimme die Wahrscheinlichkeit, dass er dabei eine Testfahrt gewonnen hat.
Bestimme die Wahrscheinlichkeit, dass er dabei eine Testfahrt gewonnen hat.
2
1.3
Der Veranstalter rechnet mit 240 Besuchern, die das Glücksrad drehen.
Bestimme die zu erwartende Anzahl benötigter Maskottchen.
Ermittle die Wahrscheinlichkeit dafür, dass mindestens 80 aber höchstens 100 Maskottchen benötigt werden.
Bestimme die zu erwartende Anzahl benötigter Maskottchen.
Ermittle die Wahrscheinlichkeit dafür, dass mindestens 80 aber höchstens 100 Maskottchen benötigt werden.
3
1.4
Ermittle die minimale Anzahl von Besuchern, die das Glücksrad drehen müssten, damit mit einer Wahrscheinlichkeit von mehr als 
mindestens zwei Besucher eine Testfahrt gewinnen.
4
1.5
Die Ausgaben des Veranstalters für eine Testfahrt übertreffen seine Ausgaben für ein Maskottchen um einen Euro, während seine Ausgaben für ein Maskottchen die durchschnittlichen Ausgaben des Veranstalters pro Spiel um 1,75 Euro übertreffen. Weitere Ausgaben, etwa für Anschaffung, Wartung und Betrieb des Glücksrades, sind hierbei nicht berücksichtigt.
Bestimme die Ausgaben für ein Maskottchen.
Bestimme die Ausgaben für ein Maskottchen.
3
15
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Bei jedem Dreh gelten folgende Wahrscheinlichkeiten:
Damit folgt:
Für Ereignis 
muss entweder der erste, der zweite oder der dritte Besucher eine Testfahrt gewinnen. Bei den anderen beiden Besuchern ist jeweils egal, ob sie ein Maskottchen oder nichts gewinnen.
1.2
Gesucht ist die bedingte Wahrscheinlichkeit 
Es gibt insgesamt vier Felder mit einem Gewinn und eines davon ist die Testfahrt. Also gilt 
Mit einer Wahrscheinlichkeit von 
handelt es sich bei einem Gewinn um eine Testfahrt.
1.3
Zu erwartende Anzahl benötigter Maskottchen bestimmen
Die zufällige Anzahl der benötigten Maskottchen wird durch die Zufallsgröße 
beschrieben, die binomialverteilt ist mit 
und 
Mit der Formel für den Erwartungswert einer binomialverteilten Zufallsgröße folgt:
Die zu erwartende Anzahl benötigter Maskottchen beträgt also 
Wahrscheinlichkeit ermitteln
![\(\begin{array}[t]{rll}
& P(80\leq X \leq 100)\\[5pt]
=& P(X\leq 100) - P(X\leq 79) \\[5pt]
\approx& 0,9185 - 0,0799 \\[5pt]
=& 0,8386 \\[5pt]
=& 83,86\,\%
\end{array}\)](https://mathjax.schullv.de/838b7c2b5ca520c7a821a7c60af380dda71cc8a6b82a8d1429fd3045f4566bdb?color=5a5a5a)
Mit einer Wahrscheinlichkeit von ca. 
werden mindestens 
aber höchstens 
Maskottchen benötigt.
1.4
Die zufällige Anzahl der gewonnenen Testfahrten wird durch die Zufallsgröße 
beschrieben, die binomialverteilt ist mit unbekanntem 
und 
Gesucht ist das kleinste 
für das 
erfüllt ist. Dies lässt sich umformen:
![\(\begin{array}[t]{rll}
P(Y_n \geq 2) &\gt & 0,9 \\[5pt]
1-P(Y_n \leq 1) &\gt & 0,9 &\quad \scriptsize \mid\;-1;\cdot (-1) \\[5pt]
P(Y_n \leq 1) &\lt & 0,1 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/4a0aeefc9231d92e2c4198345e9a06884c4efa29b1d3e7067b71697fa9697ca8?color=5a5a5a)
Durch Ausprobieren lassen sich mit dem Taschenrechner folgende Werte bestimmen:
Mindestens 
Besucher müssen das Glücksrad drehen, damit mit einer Wahrscheinlichkeit von mehr als mindestens zwei Testfahrten gewonnen werden.
1.5
Die durchschnittlichen Ausgaben für ein Spiel werden mit 
bezeichnet.
Die Ausgaben für ein Maskottchen sind dann
Die Ausgaben für eine Testfahrt sind dann
Mit der Formel für den Erwartungswert der Ausgaben für ein Spiel folgt:
Die Ausgaben für ein Maskottchen betragen also 
Die Ausgaben für ein Maskottchen sind dann
Die Ausgaben für eine Testfahrt sind dann