Analysis
1
Gegeben ist die Funktion  mit
mit  ;
;  .
.
Das Schaubild von ist
ist 
Das Schaubild von
1.1
Überprüfe, ob dies die Punkte
2
1.2
Zeige, dass für die erste Ableitung  von
von  gilt:
gilt:  Ermittle die Koordinaten und die Art des Extrempunktes von
Ermittle die Koordinaten und die Art des Extrempunktes von 
4
1.3
Zeichne  für
für 
3
1.4
Prüfe, ob die folgende Aussage wahr oder falsch ist:
„Der Inhalt der Fläche, die  mit den Koordinatenachsen im 1. Quadranten einschließt, ist das Doppelte des Mittelwertes von
mit den Koordinatenachsen im 1. Quadranten einschließt, ist das Doppelte des Mittelwertes von  auf dem Intervall
auf dem Intervall ![\([0;\ln(4)].\)](https://mathjax.schullv.de/68d355da6ef4fabc3bc6bbb42bdaa4e2a8d354f78e7311c460dee9123c7470c9?color=5a5a5a) “
“
3
1.5
Die Gerade mit der Gleichung  schneidet
schneidet  in zwei Punkten
in zwei Punkten  und
und  mit
mit  und
und 
1.5.1
Gib alle möglichen Werte für  an.
an.
2
1.5.2
Es gilt nun 
Zeige, dass dann die y-Achse die Strecke halbiert.
halbiert.
Zeige, dass dann die y-Achse die Strecke
4
1.6
Untersuche, ob das Schaubild der auf  definierten Funktion
definierten Funktion  mit
mit
 symmetrisch ist.
Gib gegebenenfalls die Art der Symmetrie an.
symmetrisch ist.
Gib gegebenenfalls die Art der Symmetrie an.
2
20
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1
Eine Punktprobe mit  ergibt:
ergibt:
![\(\begin{array}[t]{rll}
3&=&-\mathrm{e}^{2\cdot0} + 4 \mathrm{e}^0\\[5pt]
3&=&3
\end{array}\)](https://mathjax.schullv.de/34ff4c33668969f5baf5de094dc24d3fd631523fb7e0db3f57eb5c1bc6c791fe?color=5a5a5a) Eine Punktprobe mit
Eine Punktprobe mit  ergibt:
ergibt:
![\(\begin{array}[t]{rll}
0&=&-\mathrm{e}^{2\cdot \ln(4)} + 4\mathrm{e}^{\ln(4)} \\[5pt]
0&=&-4^2 + 4\cdot 4 \\[5pt]
0&=& 0
\end{array}\)](https://mathjax.schullv.de/56fc49a2a416f144603ba8bb76176f9c68daba7df7efe177b2cf7bcdd1ffd409?color=5a5a5a) Die Gleichungen führen beide zu wahren Aussagen und somit sind die angegebenen Punkte die Schnittpunkte von
Die Gleichungen führen beide zu wahren Aussagen und somit sind die angegebenen Punkte die Schnittpunkte von  mit den Koordinatenachsen.
mit den Koordinatenachsen.
1.2
1.3
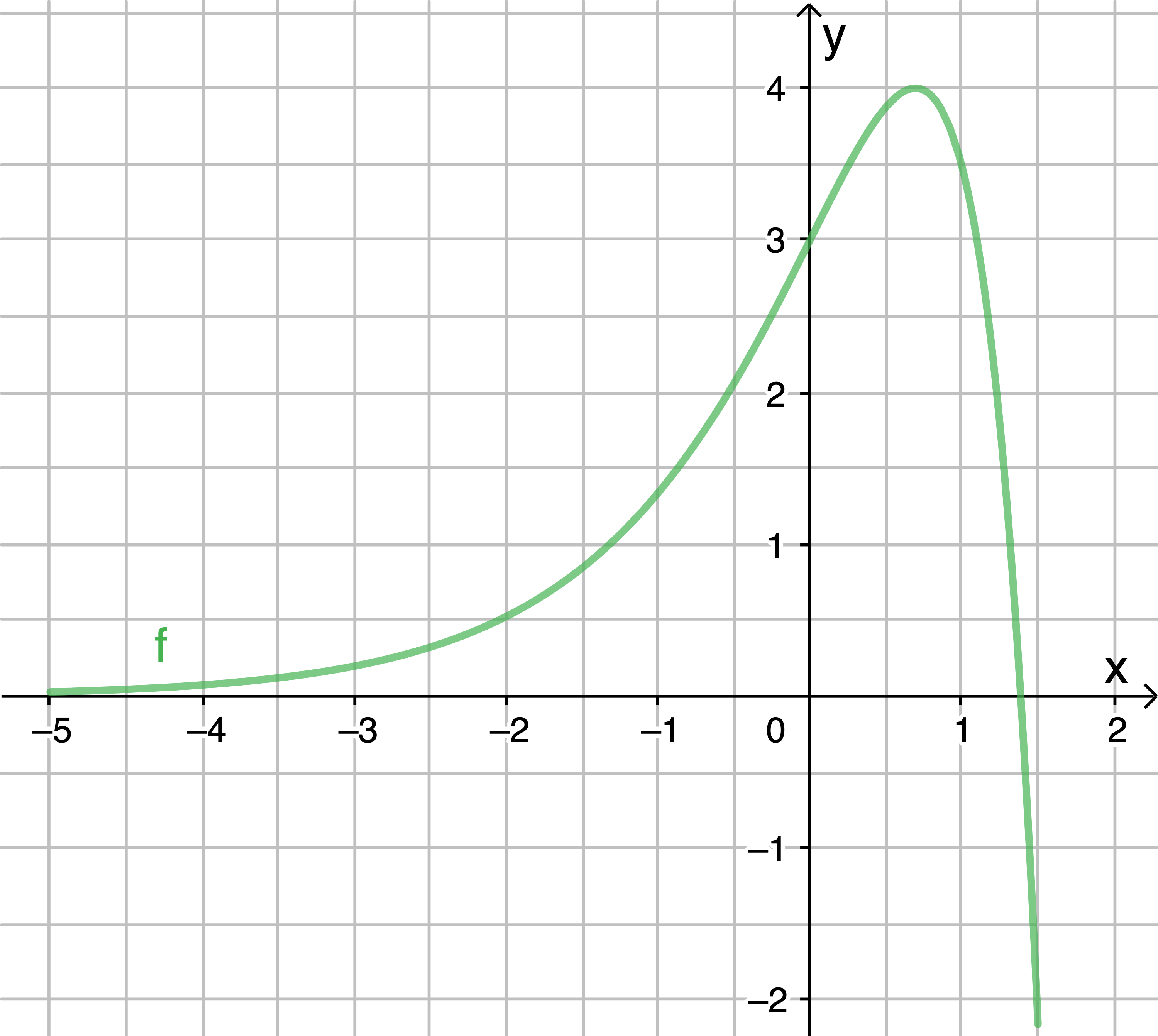
1.4
Für den Flächeninhalt gilt:
 Für den Mittelwert der Funktion
Für den Mittelwert der Funktion  im Intervall
im Intervall ![\([0, \ln(4)]\)](https://mathjax.schullv.de/c6adb05ce5e9f5053b4538bcc775769fd335a285a2c75c3b3c7e496251bb9619?color=5a5a5a) gilt:
gilt:

 Somit ist die Aussage falsch, da der Flächeninhalt das
Somit ist die Aussage falsch, da der Flächeninhalt das  -fache des Mittelwerts ist.
-fache des Mittelwerts ist.
1.5.1
Die Gerade  ist eine waagrechte Gerade auf der Höhe
ist eine waagrechte Gerade auf der Höhe  Für
Für  schneidet die waagrechte Gerade das Schaubild K in zwei Punkten, wobei ein x-Wert negativ und ein x-Wert positiv ist.
schneidet die waagrechte Gerade das Schaubild K in zwei Punkten, wobei ein x-Wert negativ und ein x-Wert positiv ist.
1.5.2
1.6