Vektorgeometrie 1

Gegeben sind die Punkte $A(6\mid 0\mid 4),$ $B(2\mid 2\mid 0),$ $C(0\mid 6\mid 4)$ und $D(4\mid 4\mid 8)$ sowie der Punkt $S(-1\mid -1\mid 6).$
Die Ebene $E: 2 x_1+2 x_2-x_3=8$ enthält die Punkte $A, B, C$ und $D.$

1.1

Zeige, dass das Viereck $A B C D$ ein Quadrat ist.

1.2

Zeichne die Pyramide $ABCDS$ in ein geeignetes Koordinatensystem.

1.3

Der Punkt $M$ ist der Schnittpunkt der Diagonalen von $ABCD.$
Zeige, dass die Strecke $MS$ orthogonal zu $E$ ist und dass die Höhe der Pyramide ABCDS 6 Längeneinheiten beträgt.

1.4

Begründe, dass alle Pyramiden mit der Grundfläche $A B C D,$ deren Spitzen zudem auf der Geraden $g$ mit

$g: \vec{x}=\begin{pmatrix} -1 \\ -1 \\ 6 \end{pmatrix}+t \cdot\begin{pmatrix} -1 \\ 1 \\ 0 \end{pmatrix};$ $t \in \mathbb{R}$

liegen, das gleiche Volumen haben.

1.5

Die Spitze $H$ der Pyramide $ABCDH$ liegt auf der Geraden $h$ mit

$h: \vec{x}=\begin{pmatrix} -1 \\ -1 \\ 6 \end{pmatrix}+t \cdot\begin{pmatrix} 3 \\ 5 \\ -2 \end{pmatrix};$ $t \in \mathbb{R}$

Das Volumen der Pyramide $A B C D H$ ist doppelt so groß wie das Volumen der Pyramide $ABCDS.$ Ermittle die Koordinaten eines solchen Punktes $H.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Rechenweg anzeigen

$\overrightarrow{AB} = \pmatrix{ -4\\2 \\ -4}$

$\overrightarrow{DC} = \pmatrix{ -4\\2 \\ -4}$

$\overrightarrow{BC} = \pmatrix{ -2\\4 \\ 4}$

$\overrightarrow{AD} = \pmatrix{-2\\4 \\ 4}$

Es gilt also $\overrightarrow{AB} = \overrightarrow{DC}$ und $\overrightarrow{BC} = \overrightarrow{AD}.$ Die jeweils gegenüberliegenden Seiten von $ABCD$ sind also parallel und gleich lang.

$\left|\overrightarrow{AB} \right|$ $= \sqrt{(-4)^2 +2^2 +(-4)^2} = 6 \;\text{[LE]}$

$\left|\overrightarrow{BC} \right|$ $= \sqrt{(-2)^2 +4^2 +4^2} = 6 \;\text{[LE]}$

Damit sind alle Seiten von $ABCD$ gleich lang.

Damit es sich um ein Quadrat handelt muss es noch einen rechten Winkel geben. Überprüfung mit Hilfe des Skalarprodukts:

$\begin{array}[t]{rll} &\overrightarrow{AB} \circ\overrightarrow{BC}\\[5pt] =& \pmatrix{ -4\\2 \\ -4} \circ \pmatrix{ -2\\4 \\ 4} \\[5pt] =& (-4)\cdot (-2) + 2 \cdot 4 +(-4)\cdot 4 \\[5pt] =& 0 \\[5pt] \end{array}$

Im Punkt $B$ besitzt $ABCD$ also einen rechten Winkel. Damit müssen aufgrund der Parallelität aller Seiten auch alle anderen Innenwinkel rechte Winkel sein. Insgesamt handelt es sich damit bei $ABCD$ um ein Quadrat.

1.2

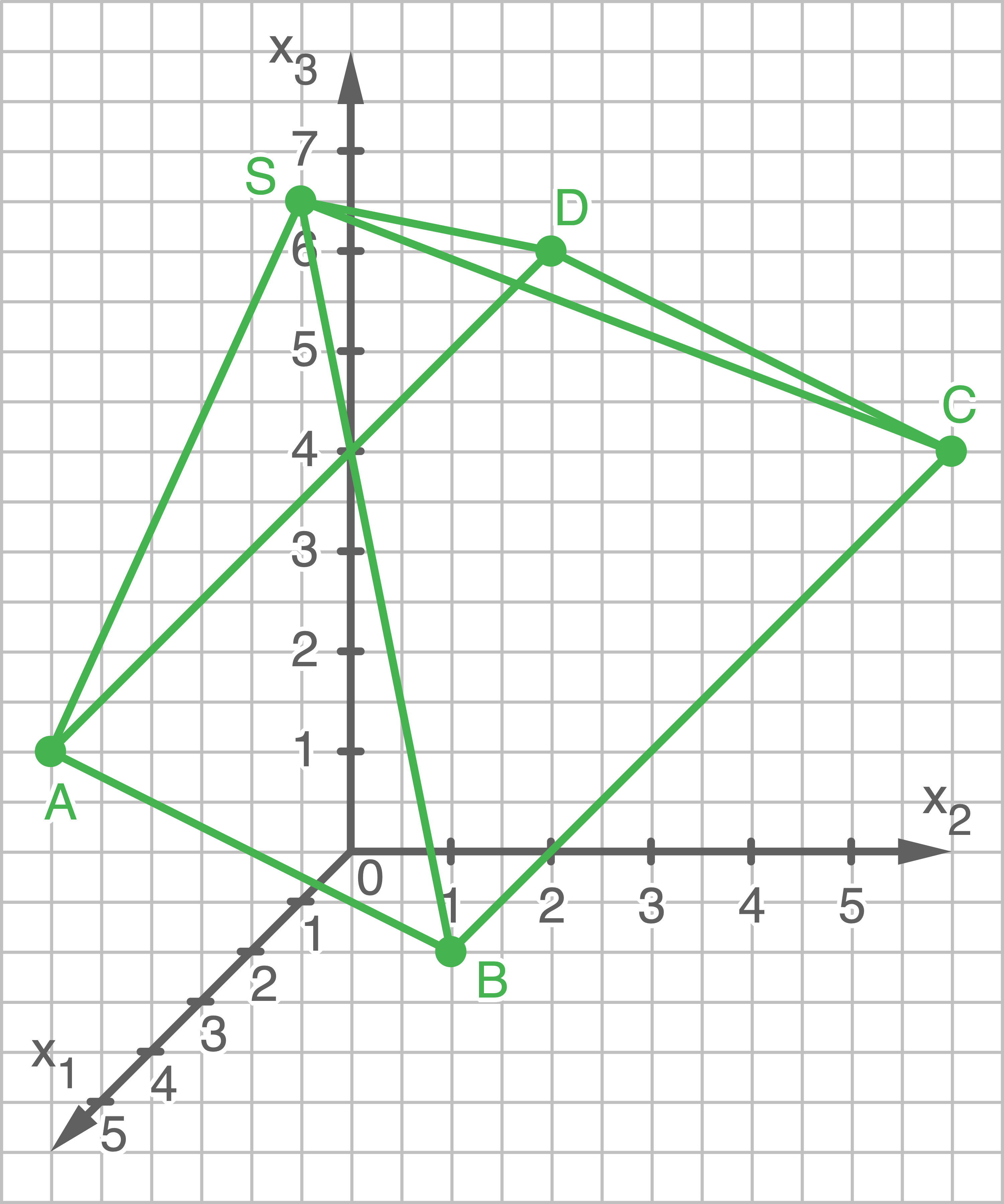
Pyramide - Baden-Württemberg berufliches Abi 2023

1.3

In einem Quadrat schneiden sich die Diagonalen in ihrem Mittelpunkt. Mit der Formel für den Ortsvektor des Mittelpunkts von $AC$ ergibt sich:

$\overrightarrow{OM} = \dfrac{1}{2}\cdot \left(\overrightarrow{OA}+\overrightarrow{OC} \right)$ $=\dfrac{1}{2}\cdot \left( \pmatrix{6\\0\\4} + \pmatrix{0\\6\\4} \right) = \pmatrix{3\\3\\4}$

$\overrightarrow{MS} = \overrightarrow{OS} - \overrightarrow{OM}$ $= \pmatrix{-1\\-1\\6}- \pmatrix{3\\3\\4} = \pmatrix{-4\\-4\\2}$

Aus der Ebenengleichung von $E$ lässt sich ein Normalenvektor ablesen: $\overrightarrow{n} = \pmatrix{2\\2\\-1}.$

Es gilt $\overrightarrow{MS} = -2\cdot \overrightarrow{n}.$

Diese beiden Vektoren sind also linear abhängig. Somit ist $\overrightarrow{MS}$ orthogonal zu $E.$

Für die Höhe der Pyramide gilt aufgrund der Orthogonalität:

$h= \left|\overrightarrow{MS} \right| = \sqrt{(-4)^2 +(-4)^2 +2^2} = 6\,\text{[LE]}$

1.4

Für den Richtungsvektor $\overrightarrow{r} = \pmatrix{-1\\1\\0}$ von $g$ und den Normalenvektor $\overrightarrow{n} = \pmatrix{2\\2\\-1}$ von $E$ gilt:

$\begin{array}[t]{rll} \overrightarrow{n} \circ \overrightarrow{r}&=& \pmatrix{2\\2\\-1}\circ\pmatrix{-1\\1\\0} \\[5pt] &=& 2\cdot (-1) +2\cdot 1 +(-1)\cdot 0 \\[5pt] &=& 0\\[5pt] \end{array}$

Die Gerade $g$ verläuft also orthogonal zum Normalenvektor von $E$ und ist somit parallel zu $E.$

Alle Punkte auf $g$ haben daher denselben Abstand von $E.$ Da dieser Abstand jeweils der Höhe der beschriebenen Pyramide entspricht, haben alle Pyramiden mit der Grundfläche $ABCD,$ deren Spitze auf der Geraden $g$ liegen, die gleiche Höhe und damit auch das gleiche Volumen.

1.5