Vektorgeometrie 2

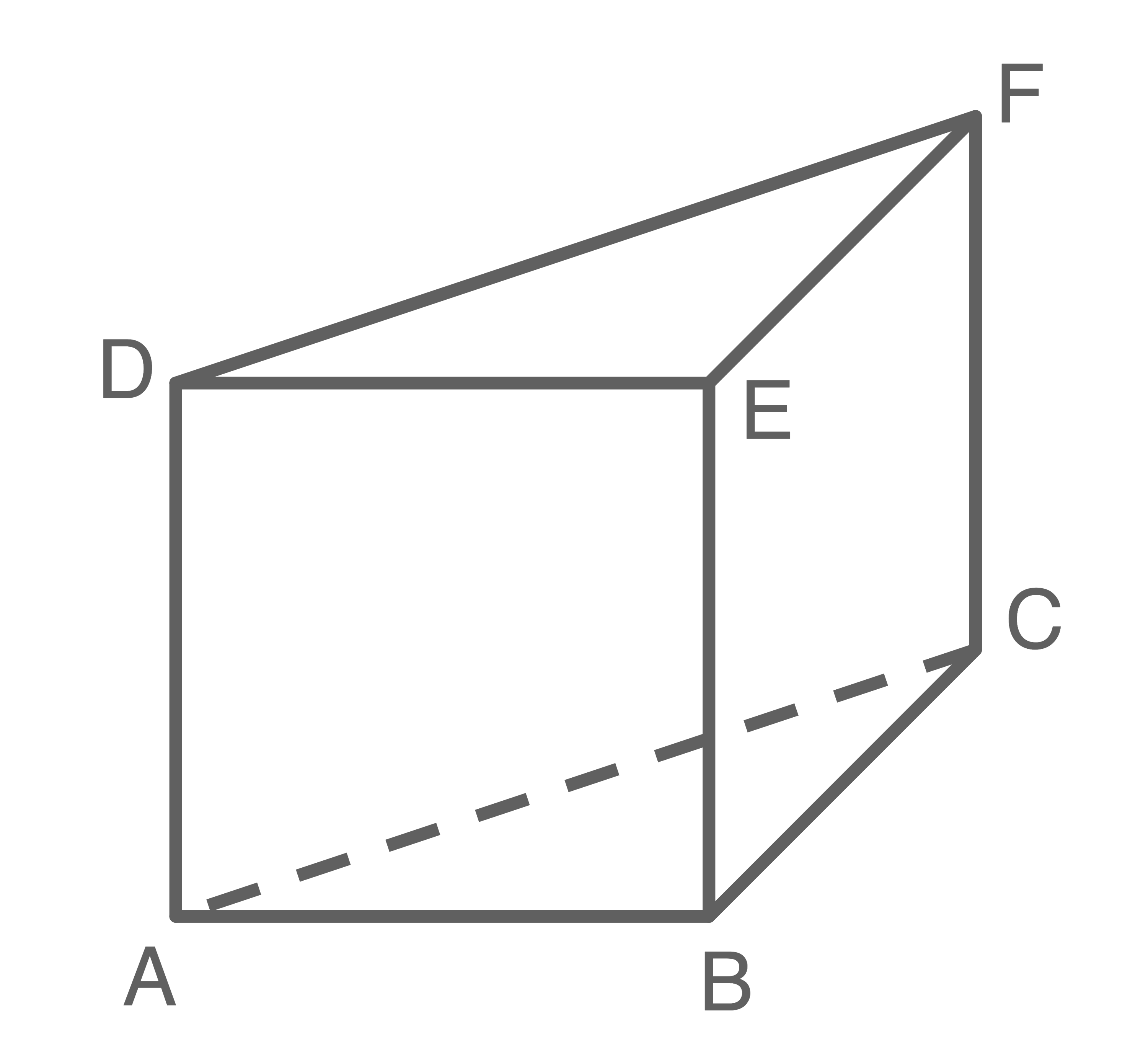
Gegeben sind die Eckpunkte $A(2\mid 0\mid 0),$ $B(2\mid 2\mid 0),$ $C(0\mid 2\mid 0),$ $D(2\mid 0\mid 2)$ eines Prismas mit der Grundfläche $A B C$ und den zu dieser Fläche senkrechten Kanten $A D,$ $BE$ und $CF.$

Dreiecksprisma - Berufliches Gymnasium Abi 2023 Baden-Württemberg

3.1

Zeige, dass das Dreieck $ABC$ rechtwinklig ist.
Berechne das Volumen des Prismas.

3.2

Die Gerade $g$ mit

$g: \vec{x}=\begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix}+s \cdot\begin{pmatrix} 1 \\ -2 \\ 2 \end{pmatrix};$ $\quad s \in \mathbb{R}$

enthält einen Eckpunkt und den Mittelpunkt einer Kante des Prismas.
Bestimme diese beiden Punkte.

3.3

Die Gerade $h$ ist gegeben durch

$h: \vec{x}=\begin{pmatrix}2 \\ 1 \\ 0\end{pmatrix}+r \cdot \begin{pmatrix}-2 \\ 1 \\ 2\end{pmatrix};\quad$ $r \in \mathbb{R}.$

Untersuche, ob sich die Geraden $g$ und $h$ schneiden.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

3.1

Rechtwinkligkeit zeigen

Die Skizze lässt erahnen, dass sich der rechte Winkel im Punkt $B$ befindet. Dafür muss $\overrightarrow{BA}\circ \overrightarrow{BC} =0$ gelten.

$\begin{array}[t]{rll} &\overrightarrow{BA}\circ \overrightarrow{BC} \\[5pt] =& \left(\overrightarrow{OA}-\overrightarrow{OB}\right)\circ \left(\overrightarrow{OC}-\overrightarrow{OB}\right)\\[5pt] =& \left( \pmatrix{2\\0\\0} - \pmatrix{2\\2\\0}\right) \circ \left( \pmatrix{0\\2\\0} - \pmatrix{2\\2\\0}\right) \\[5pt] =& \pmatrix{0\\2\\0} \circ \pmatrix{-2\\0\\0}\\[5pt] =& 0\cdot (-2) + 2\cdot 0 + 0 \cdot 0\\[5pt] =& 0 \end{array}$

Im Punkt $B$ besitzt das Dreieck $ABC$ also einen rechten Winkel.

Volumen des Prismas berechnen

Aufgrund des rechten Winkels bei $B$ und weil die Kanten $AD,$ $BE$ und $CF$ senkrecht zur Grundfläche verlaufen, kann das Volumen wie folgt berechnet werden:

$V_{\text{Prisma}} = \dfrac{1}{2}\cdot \left|\overrightarrow{BA} \right| \cdot \left|\overrightarrow{BC} \right| \cdot \left|\overrightarrow{BE} \right|$

Da es sich um ein Prisma handelt sind die Kanten $AD,$ $BE$ und $CF$ gleich lang. Also folgt:

$\begin{array}[t]{rll} \left| \overrightarrow{BA}\right| &=& \left| \pmatrix{0\\2\\0} \right| \\[5pt] &=& \sqrt{0^2 + 2^2 +0^2} \\[5pt] &=& 2 \\[5pt] \end{array}$

$\begin{array}[t]{rll} \left| \overrightarrow{BC}\right| &=& \left| \pmatrix{-2\\0\\0} \right| \\[5pt] &=& \sqrt{(-2)^2 + 0^2 +0^2} \\[5pt] &=& 2 \\[5pt] \end{array}$

$\begin{array}[t]{rll} \left| \overrightarrow{AD}\right| &=& \left| \pmatrix{2\\0\\2} - \pmatrix{2\\0\\0}\right| \\[5pt] &=& \left| \pmatrix{0\\0\\2} \right| \\[5pt] &=& \sqrt{0^2 + 0^2 +2^2} \\[5pt] &=& 2 \\[5pt] \end{array}$

$V_{\text{Prisma}}= \dfrac{1}{2}\cdot 2\cdot 2\cdot 2$ $= 4\,\text{[VE]}$

3.2

Durch Ausprobieren ergibt sich für $s=1:$

$\pmatrix{1\\2\\0} + 1 \cdot \pmatrix{1\\-2\\2} = \pmatrix{2\\0\\2}$

Dies entspricht dem Ortsvektor von $D.$ Der Eckpunkt $D$ liegt also auf $g.$

Der Stützpunkt $(1\mid 2\mid 0)$ entspricht dem Mittelpunkt der Kante $BC:$

$\overrightarrow{OM_{BC}} = \frac{1}{2}\cdot \left(\overrightarrow{OB} + \overrightarrow{OC} \right)$ $= \frac{1}{2}\cdot \left(\pmatrix{2\\2\\0} + \pmatrix{0\\2\\0} \right) = \pmatrix{1\\ 2\\0}$

Auf $g$ liegen also der Eckpunkt $D(2\mid 0\mid 2)$ und der Mittelpunkt der Kante $BC$ mit den Koordinaten $(1\mid 2\mid 0).$

3.3

1. Schritt: Parallelität überprüfen

Wenn $g$ und $h$ parallel wäre, müssten die beiden Richtungsvektoren linear abhängig sein. Es müsste also einen Faktor $a\in \mathbb{R}$ geben, für den

$a\cdot \pmatrix{1\\-2\\2} = \pmatrix{-2\\1\\2}$

gilt.

Die erste Zeile dieser Gleichung wäre für $a=-2$ erfüllt, was in der zweiten Zeile allerdings zu einem Widerspruch führt.

Die Richtungsvektoren sind also nicht linear abhängig und $g$ und $h$ damit weder identisch noch parallel.

2. Schritt: Auf Schnittpunkt überprüfen

Gleichsetzen der beiden Geradengleichungen liefert folgende Gleichung:

Rechenweg anzeigen

$\pmatrix{-1\\1\\0} =r \cdot \begin{pmatrix}-2 \\ 1 \\ 2\end{pmatrix} - s \cdot \pmatrix{1\\-2\\2}$

Daraus ergibt sich folgendes Gleichungssystem mit zwei Variablen:

$\begin{array}{lrll} \text{I}\quad& -1 &=& -2r -s \\ \text{II}\quad& 1 &=& r+2s \\ \text{III}\quad& 0 &=& 2r-2s \\ \end{array}$

Aus der dritten Gleichung folgt:

$\begin{array}[t]{rll} 0 &=& 2r-2s &\quad \scriptsize \mid\; +2s \\[5pt] 2s&=& 2r &\quad \scriptsize \mid\; :2\\[5pt] s&=& r \end{array}$

Das kann nun in die zweite Gleichung eingesetzt werden:

$\begin{array}[t]{rll} 1 &=& r+2s &\quad \scriptsize \mid\; s=r \\[5pt] 1 &=& r+2r \\[5pt] 1 &=& 3r &\quad \scriptsize \mid\; :3 \\[5pt] \frac{1}{3} &=& r \end{array}$

Einsetzen in die erste Gleichung liefert:

$\begin{array}[t]{rll} -1 &=& -2r -s &\quad \scriptsize \mid\; s=r; r=\frac{1}{3} \\[5pt] -1 &=& -2\cdot \frac{1}{3}-\frac{1}{3} \\[5pt] -1 &=& -1 \end{array}$

Für $r=s=\frac{1}{3}$ ist die Gleichung erfüllt. Die beiden Geraden schneiden sich also in einem Punkt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?