Analysis

1.1

Die Funktion $f$ ist gegeben durch $f(x)=\frac{1}{2} x^3-6 x$ mit $x \in \mathbb{R}.$
Das Schaubild von $f$ ist $K_f.$
Bestimme die Koordinaten und die Art der Extrempunkte von $K_f.$
Gib die Koordinaten des Wendepunkts von $K_{f}$ an.

1.2

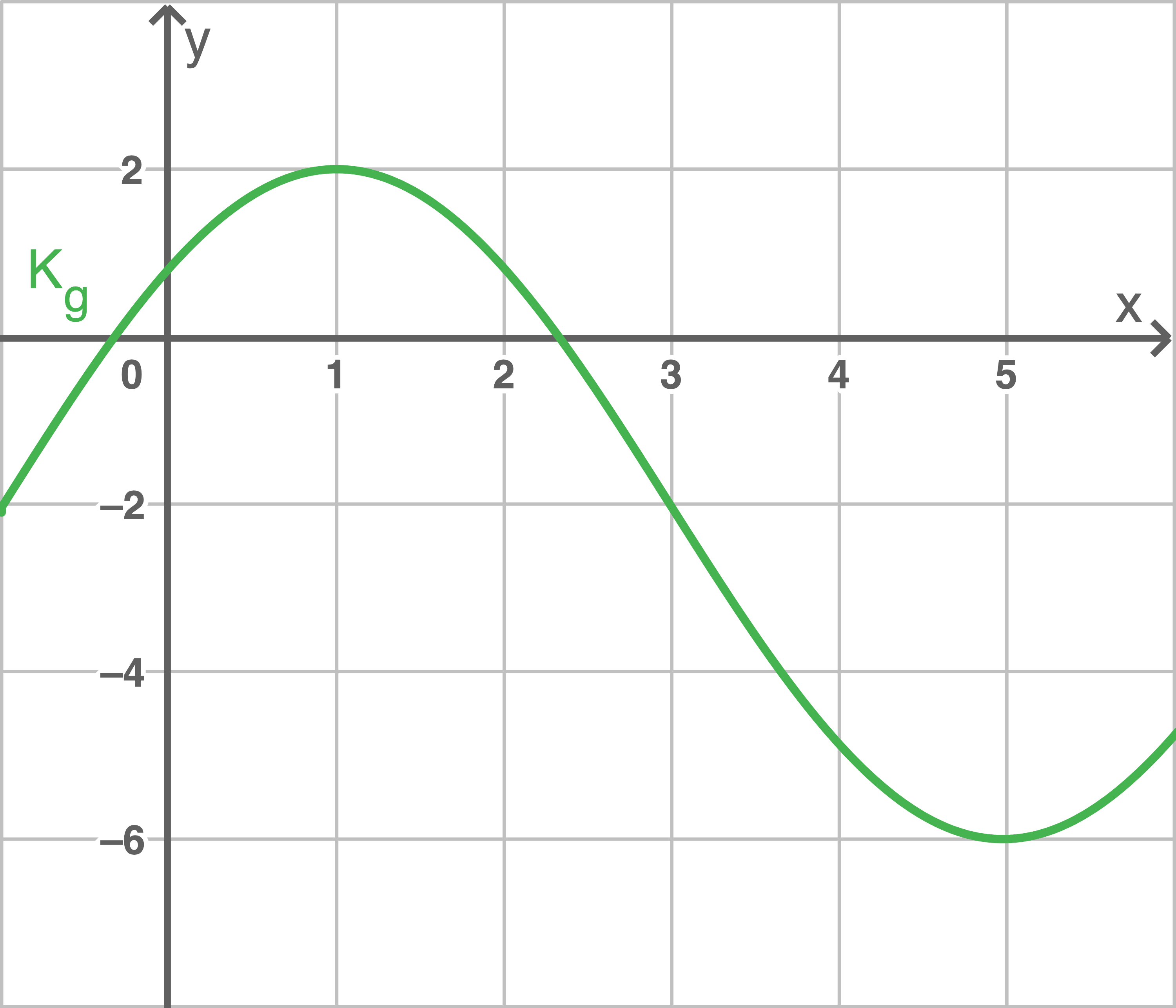
Die Abbildung zeigt einen Ausschnitt des Schaubilds $K_g$ einer Funktion $g.$
Entscheide, ob folgende Aussagen wahr oder falsch sind.
Begründe jeweils deine Entscheidung.

(1)

$g(5)-g(3)\lt -5$

(2)

$g^{\prime}(4)\lt 0$

(3)

Für jede Stammfunktion $G$ von $g$ gilt: $G(3)-G(0)\gt 0.$

Funktionsgraph - Berufliches Gymnasium Abi 2023 Baden-Württemberg

1.3

Eine in $\mathbb{R}$ definierte Cosinusfunktion $h$ hat die Periodenlänge $p.$
Der Punkt $\left(\frac{p}{2} \mid p\right)$ ist ein Hochpunkt des Graphen von $h,$ der Punkt $\left(\frac{p}{4} \mid \frac{p}{2}\right)$ ein Wendepunkt.
Bestimme die Steigung von $h$ an der Stelle $\frac{p}{4}.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Koordinaten und Art der Extrempunkte bestimmen

1. Schritt: Ableitungsfunktionen bestimmen

$\(\begin{array}[t]{rll} f(x) &=& \dfrac{1}{2}x^3 -6x \\[5pt] f$

2. Schritt: Notwendiges Kriterium für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

3. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen und Art der Extremstellen bestimmen

$\(\begin{array}[t]{rll} f$

4. Schritt: $\boldsymbol{y}$ -Koordinaten ermitteln

$\begin{array}[t]{rll} f(-2)&=& \dfrac{1}{2}\cdot (-2)^3 -6\cdot (-2) \\[5pt] &=& 8 \\[5pt] f(2)&=& \dfrac{1}{2}\cdot 2^3 -6\cdot 2 \\[5pt] &=& -8 \\[5pt] \end{array}$

$K_f$ besitzt einen Hochpunkt mit den Koordinaten $H(-2\mid 8)$ und einen Tiefpunkt mit den Koordinaten $T(2\mid -8).$

Koordinaten des Wendepunkts bestimmen

Da es sich bei $f$ um eine ganzrationale Funktion dritten Grades handelt, deren Funktionsterm nur ungerade Exponenten enthält, ist $K_f$ punktsymmetrisch zum Koordinatenursprung. Dadurch lauten die Koordinaten des Wendepunkts $W(0\mid 0).$

Alternativ: Rechnerisch bestimmen

1. Schritt: Notwendiges Kriterium für Wendestellen anwenden

$\(\begin{array}[t]{rll} f$

Da $K_f$ zwei Extrempunkte besitzt, muss es einen Wendepunkt geben. Das notwendige Kriterium für Wendestellen ist nur für $x=0$ erfüllt, somit muss dies die Wendestelle sein. Auf die Überprüfung mit Hilfe der dritten Ableitung (Hinreichendes Kriterium) kann daher verzichtet werden.

2. Schritt: $\boldsymbol{y}$ -Koordinate berechnen

$f(0) = \dfrac{1}{2}\cdot 0^3 -6\cdot 0 = 0$

1.2

(1)

Durch Ablesen am Schaubild folgt:

$g(5)\approx -6$

$g(3)\approx -2$

$g(5)-g(3)\approx -6-(-2) = -4 \gt -5$

Die Aussage ist also falsch.

(2)

$\(g$ beschreibt die Steigung von $K_f$ an der Stelle $x=4.$

An dieser Stelle ist $K_f$ fallend. Also ist die Steigung negativ.

Diese Aussage ist also wahr.

(3)

$G(3)-G(0)$ beschreibt die Bilanz der Flächeninhalte, die $K_f$ mit der $x$ -Achse einschließt. Flächen unterhalb der $x$ -Achse fließen negativ ein, Flächen oberhalb positiv.
Im Intervall $[0;3]$ schließt $K_f$ eine größere Fläche oberhalb der $x$ -Achse mit der $x$ -Achse ein als unterhalb.
Dadurch ist die Flächenbilanz positiv und die Aussage wahr.

1.3

Für eine Cosinusfunktion mit $h(x)= a\cdot \cos(b\cdot (x-c))+d$ und der Periodenlänge $p$ gilt:

$b=\frac{2\pi}{p}$
$c$ entspricht der Verschiebung entlang der $x$ -Achse. Bei der Cosinusfunktion mit $f(x)=\cos(x)$ liegt einer der Hochpunkte bei $x=0.$
Bei $K_h$ soll ein Hochpunkt bei $x=\frac{p}{2}$ liegen. Also ist z.B. $c=-\frac{p}{2}$ möglich.
$a$ ist die Amplitudenlänge, die der Differenz der $y$ -Koordinaten von Hoch- und Wendepunkt entspricht. Also ist $a= p-\frac{p}{2} = \frac{p}{2}.$
$d$ entspricht der Verschiebung entlang der $y$ -Achse.
Damit die Hochpunkte von $K_h$ nun noch die richtigen $y$ -Koordinaten haben, wird eine Verschiebung in $y$ -Richtung um eine Amplitudenlänge benötigt. Also ist $d= \frac{p}{2}.$