Stochastik 1
2
Eine ideale Münze zeigt nach jedem Wurf entweder Kopf oder Zahl an.
2.1
Man wirft die Münze solange bis sie Zahl zeigt, jedoch höchstens dreimal.
2.1.1
Zeichne ein Baumdiagramm, das dieses Zufallsexperiment vollständig beschreibt.
2
2.1.2
Bestimme, wie oft man die Münze im Mittel wirft.
2
2.2
Entscheide, ob folgende Aussagen wahr oder falsch sind.
Begründe.
Begründe.
(1)
Wird die Münze fünfmal hintereinander geworfen, so ist die Wahrscheinlichkeit für das Ereignis „genau einmal Zahl“ größer als 
(2)
Es gibt eine Anzahl von Würfen für die Folgendes gilt:
Die Wahrscheinlichkeit für das Ereignis „genau dreimal Zahl“ ist gleich der Wahrscheinlichkeit für das Ereignis „genau zweimal Zahl“.
4
8
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
2.1.1
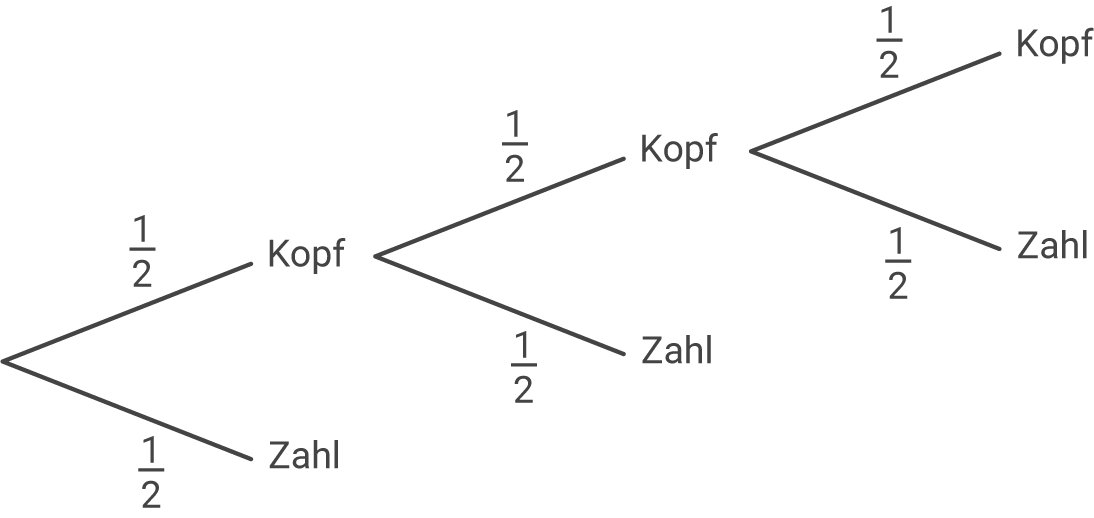
2.1.2
Wie oft die Münze geworfen wird, hängt davon ab, wann die Münze Zahl zeigt.
Im Mittel wird die Münze 1,75 mal geworfen.
- Sie wird einmal geworfen, wenn sie beim ersten Wurf Zahl zeigt.
- Sie wird zweimal geworfen, wenn sie beim ersten Wurf Kopf und beim zweiten Wurf Zahl zeigt.
- Sie wird dreimal geworfen, wenn sie beim ersten und zweiten Wurf Kopf zeigt.
2.2
(1)
Es gibt fünf mögliche Pfade für das Ereignis „genau einmal Zahl“. Mit den Pfadregeln folgt:
Die Aussage ist also wahr.
(2)
Da Kopf und Zahl bei jedem Wurf mit der gleichen Wahrscheinlichkeit gezeigt werden, sind die Wahrscheinlichkeiten für „genau dreimal Zahl“ und „genau dreimal Kopf“ gleich.
Bei fünf Würfen entspricht das Ereignis „genau dreimal Zahl“ zudem dem Ereignis „genau zweimal Kopf“ und umgekehrt entspricht das Ereignis „genau zweimal Zahl“ dem Ereignis „genau dreimal Kopf“.
Insgesamt gilt also bei fünf Würfen:
Also ist die Aussage wahr.
Bei fünf Würfen entspricht das Ereignis „genau dreimal Zahl“ zudem dem Ereignis „genau zweimal Kopf“ und umgekehrt entspricht das Ereignis „genau zweimal Zahl“ dem Ereignis „genau dreimal Kopf“.
Insgesamt gilt also bei fünf Würfen: