Anwendungsorientierte Analysis 1
2.1
In der Küche eines Hauses werden zum selben Zeitpunkt eine kleine und eine große Teekanne mit kochendem Wasser gefüllt. Die Temperaturverläufe des Wassers in 
werden durch die Funktionen 
und 
beschrieben.
Für die kleine Teekanne gilt:
Für die große Teekanne gilt:
Hierbei wird die Zeit 
in Minuten gemessen.
Der Zeitpunkt der Befüllung ist
Für die kleine Teekanne gilt:
Der Zeitpunkt der Befüllung ist
2.1.1
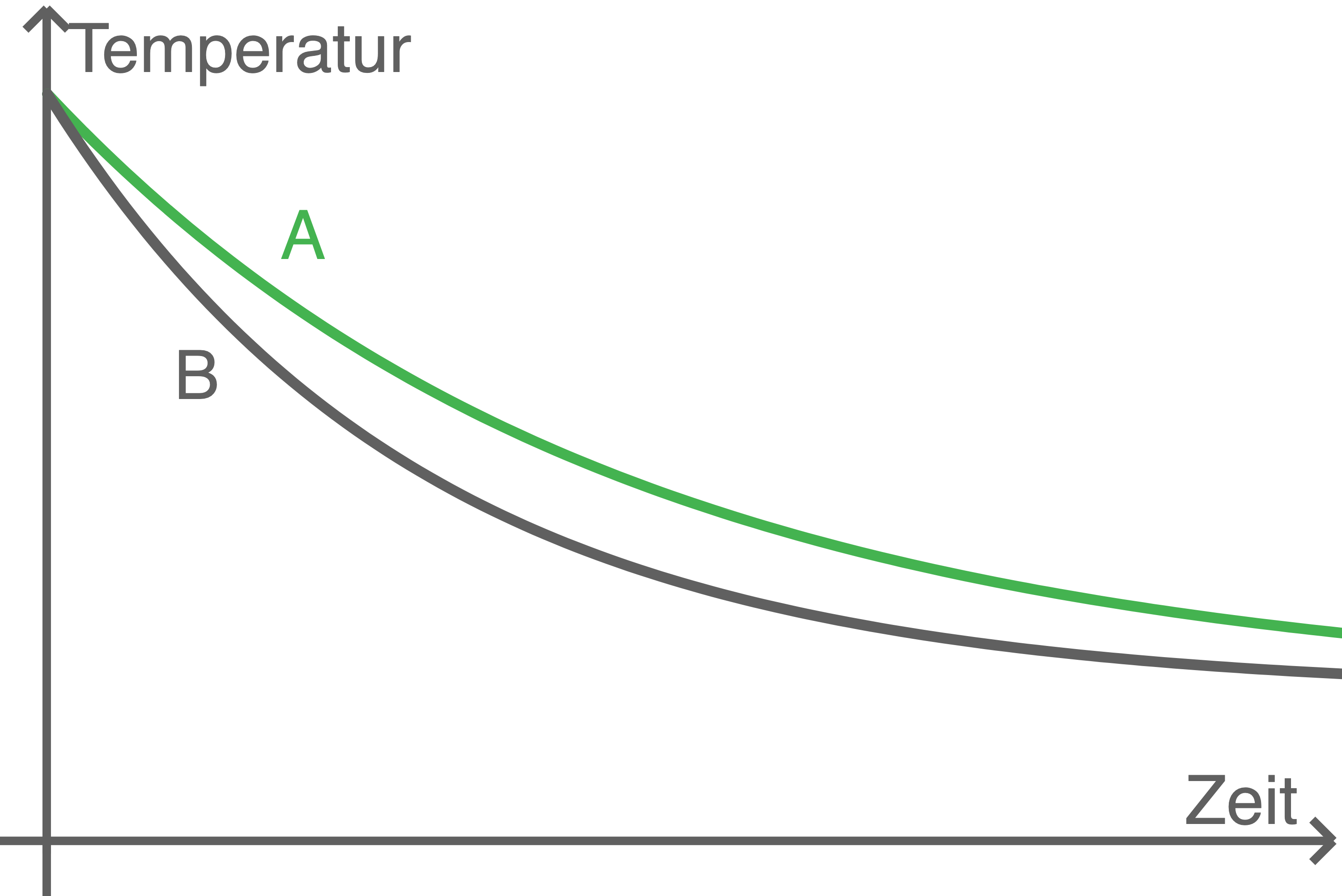
Die Temperaturverläufe sind in der nebenstehenden Abbildung dargestelit.
Ordne die Kurven 
und 
den Funktionen und zu.
Gib die Raumtemperatur in der Küche an.
Zeige: Die Wassertemperatur in der kleinen Teekanne beträgt 20 Minuten nach dem Befüllen etwa
Zeige: Die Wassertemperatur in der kleinen Teekanne beträgt 20 Minuten nach dem Befüllen etwa
3
2.1.2
Ermittle den Zeitpunkt, an dem sich die Wassertemperaturen der beiden Teekannen am stärksten voneinander unterscheiden.
4
2.2
In den Heizungskeller wird ein Eimer mit 
kaltem Wasser gestellt.
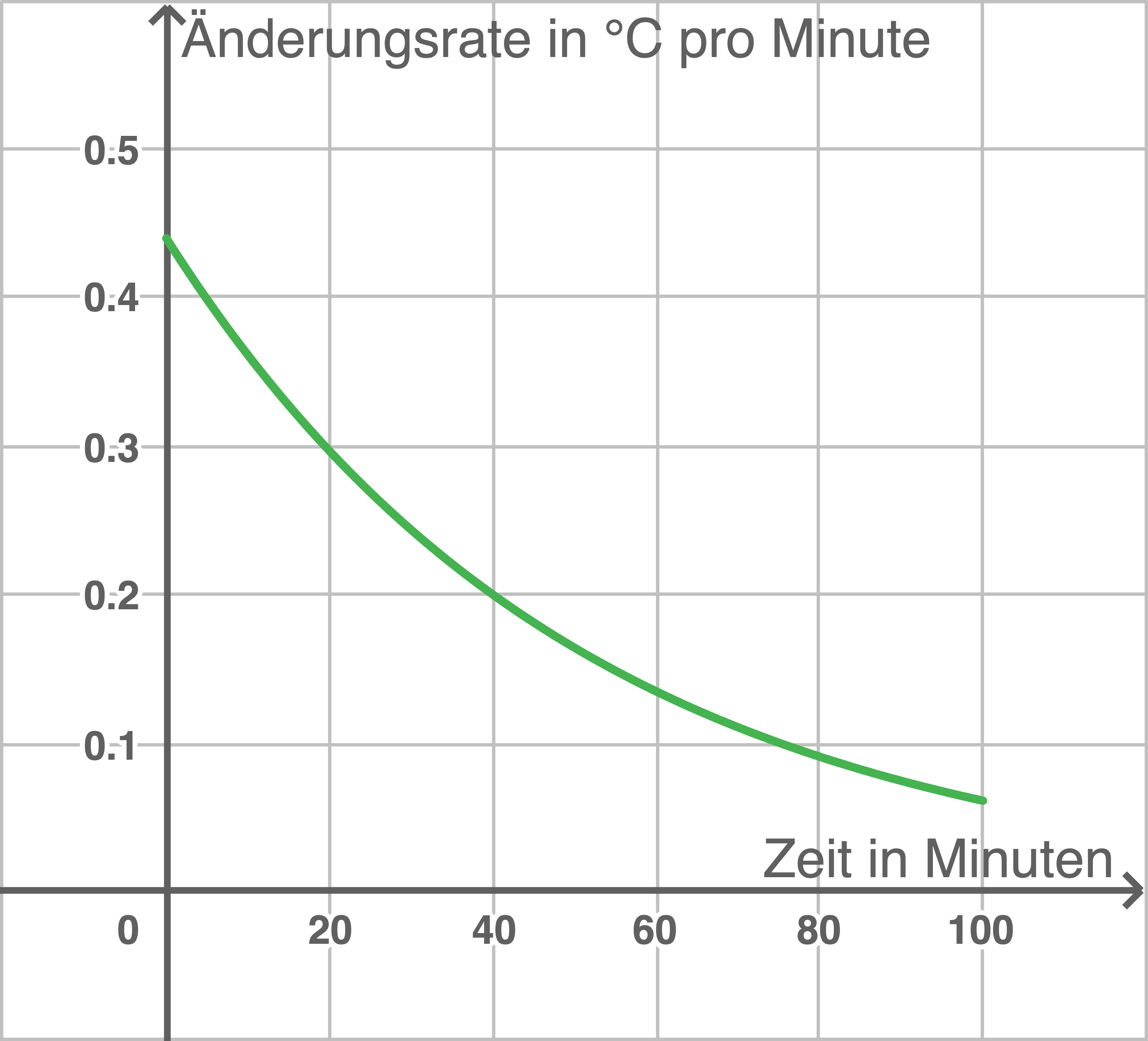
Die momentane Änderungsrate
der Wassertemperatur ab dem Zeitpunkt des Abstellens ist im Schaubild dargestellt.
Es ist bekannt:
Bestimme die Raumtemperatur im Heizungskeller.
Die momentane Änderungsrate
Es ist bekannt:
3
10
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
2.1.1
Kurven zuordnen
ablesen. Die Raumtemperatur in der Küche beträgt also 
Wassertemperatur in der kleinen Teekanne nach 20 Minuten zeigen
- Kurve A gehört zu Funktion
- Kurve B gehört zu Funktion
da die Temperaturabnahme hier schneller erfolgt.
2.1.2
1. Schritt: Funktionsterm aufstellen
Die Differenz der beiden Wassertemperaturen zum Zeitpunkt lässt sich mit folgender Funktion beschreiben:
![\(\begin{array}[t]{rll}
d(t) =& g(t) -f(t) \\[5pt]
=& 20+80\cdot \mathrm e^{-0,04t}-\left(20+80\cdot \mathrm e^{-0,06t} \right) \\[5pt]
=& 80\cdot \mathrm e^{-0,04t}- 80\cdot \mathrm e^{-0,06t}\\[5pt]
\end{array}\)](https://mathjax.schullv.de/454432db92c76b8df52a23f70cb2ce3501a8da9fa650ff85a42160839449a24e?color=5a5a5a)
Gesucht ist das Maximum von 
2. Schritt: Ableitungsfunktion bestimmen
3. Schritt: Notwendiges Kriterium für Extremstellen anwenden
Da die Wassertemperaturen zu Beginn identisch sind und sich langfristig auch dem gleichen Wert annähern, muss dies der Zeitpunkt mit der größten Differenz sein.
Ungefähr 20 Minuten nach der Befüllung unterscheiden sich die Wassertemperaturen am stärksten voneinander.
2.2
Mit Hilfe des Schaubildes wird ein Wert für 
bestimmt. Es lässt sich ablesen: 
![\(\begin{array}[t]{rll}
a(40) &\approx& 0,2 \\[5pt]
0,44\cdot \mathrm e^{b\cdot 40} &\approx& 0,2 &\quad \scriptsize \mid\;:0,44 \\[5pt]
\mathrm e^{b\cdot 40} &\approx& \frac{5}{11} &\quad \scriptsize \mid\; \ln \\[5pt]
b\cdot 40 &\approx& \ln\left(\frac{5}{11}\right) &\quad \scriptsize \mid\; :40 \\[5pt]
b &\approx& \dfrac{\ln\left(\frac{5}{11}\right)}{40}\\[5pt]
b &\approx& -0,02
\end{array}\)](https://mathjax.schullv.de/98f4222a56271cf7491a17cbfe068d6c52ab4da1817ba443ba463babb7df10a4?color=5a5a5a)
Die Wassertemperatur im Eimer wird durch eine Stammfunktion von beschrieben.
mit 
Da es sich um beschränktes Wachstum handelt, bei dem die obere Schranke 
der Raumtemperatur im Heizungskeller entspricht, muss folgende Form haben:
ist die Anfangstemperatur des Wassers im Eimer. Also muss 
und damit 
sein.
Die Raumtemperatur im Heizungskeller beträgt also ca. 