Analysis
1.1
Die Funktion  ist gegeben durch
ist gegeben durch  mit
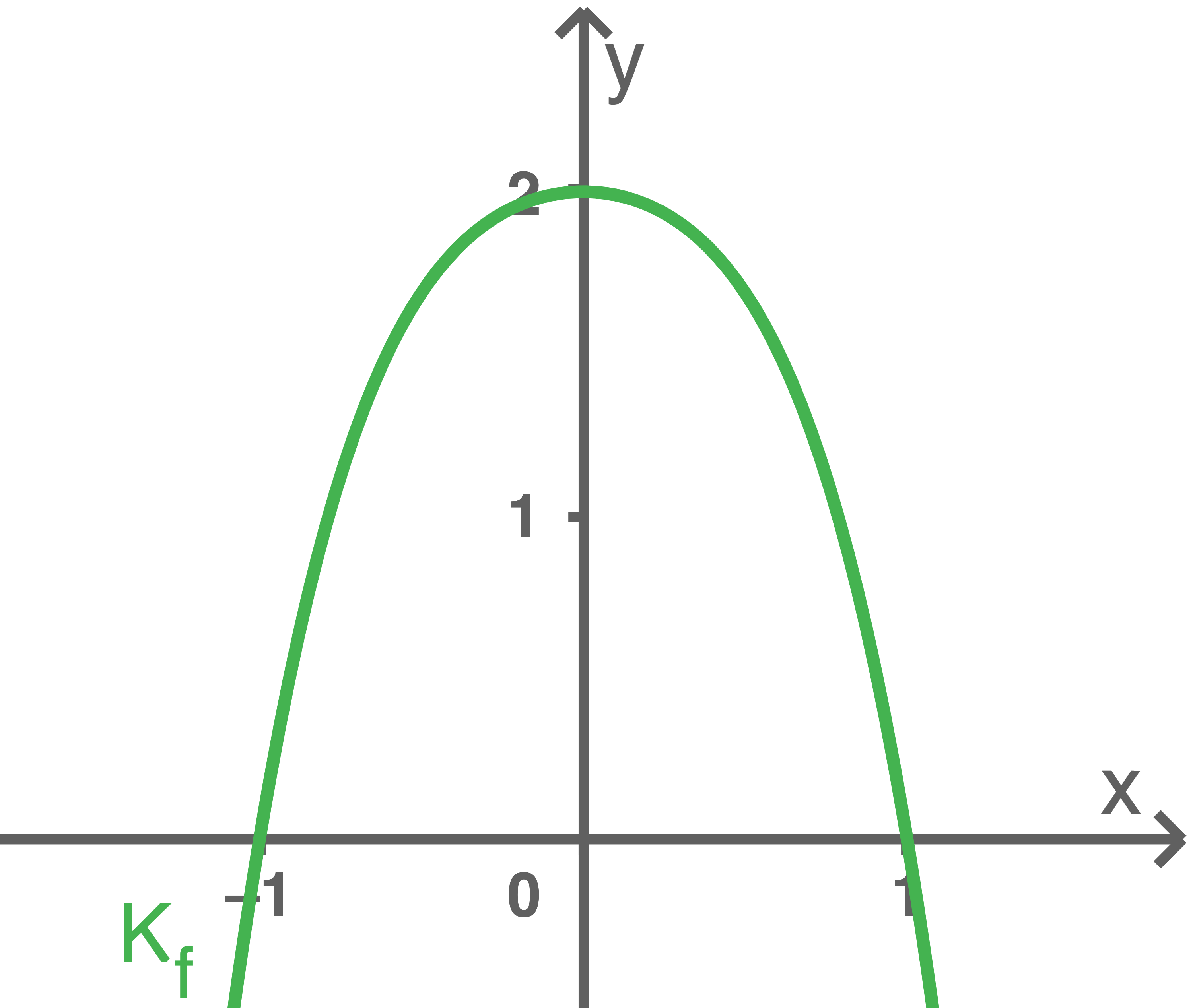
mit  Die Abbildung zeigt das Schaubild
Die Abbildung zeigt das Schaubild  von
von 
Es gilt:
Es gilt:
1.1.1
Begründe, dass  symmetrisch zur
symmetrisch zur  -Achse ist.
-Achse ist.
Bestimme den Umfang des Dreiecks, dessen Eckpunkte die Schnittpunkte von mit den Koordinatenachsen sind.
mit den Koordinatenachsen sind.
Bestimme den Umfang des Dreiecks, dessen Eckpunkte die Schnittpunkte von
4
1.1.2
Zeige, dass  keinen Wendepunkt besitzt.
keinen Wendepunkt besitzt.
2
1.1.3
Berechne den Inhalt der Fläche, die von  und den Koordinatenachsen im 1. Quadranten umschlossen wird.
und den Koordinatenachsen im 1. Quadranten umschlossen wird.
Bestimme eine Gleichung der Geraden, die durch den Hochpunkt von verläuft und diese Fläche halbiert.
verläuft und diese Fläche halbiert.
Bestimme eine Gleichung der Geraden, die durch den Hochpunkt von
4
1.2
Die Funktion  ist gegeben durch
ist gegeben durch  mit
mit 
 ist das Schaubild von
ist das Schaubild von 
1.2.1
Die Funktion  besitzt eine Nullstelle
besitzt eine Nullstelle  im Intervall
im Intervall ![\([-1 ; 0].\)](https://mathjax.schullv.de/8cc3792e74922bd27a123c9ab5a0746a323da0df9c76a60c21bdea72c4e86266?color=5a5a5a)
Bestimme die ersten beiden Nachkommastellen von
Bestimme die ersten beiden Nachkommastellen von
2
1.2.2
Ermittle, um wie viele Längeneinheiten man die Gerade mit  nach oben verschieben muss, damit die verschobene Gerade
nach oben verschieben muss, damit die verschobene Gerade  berührt.
berührt.
3
1.2.3
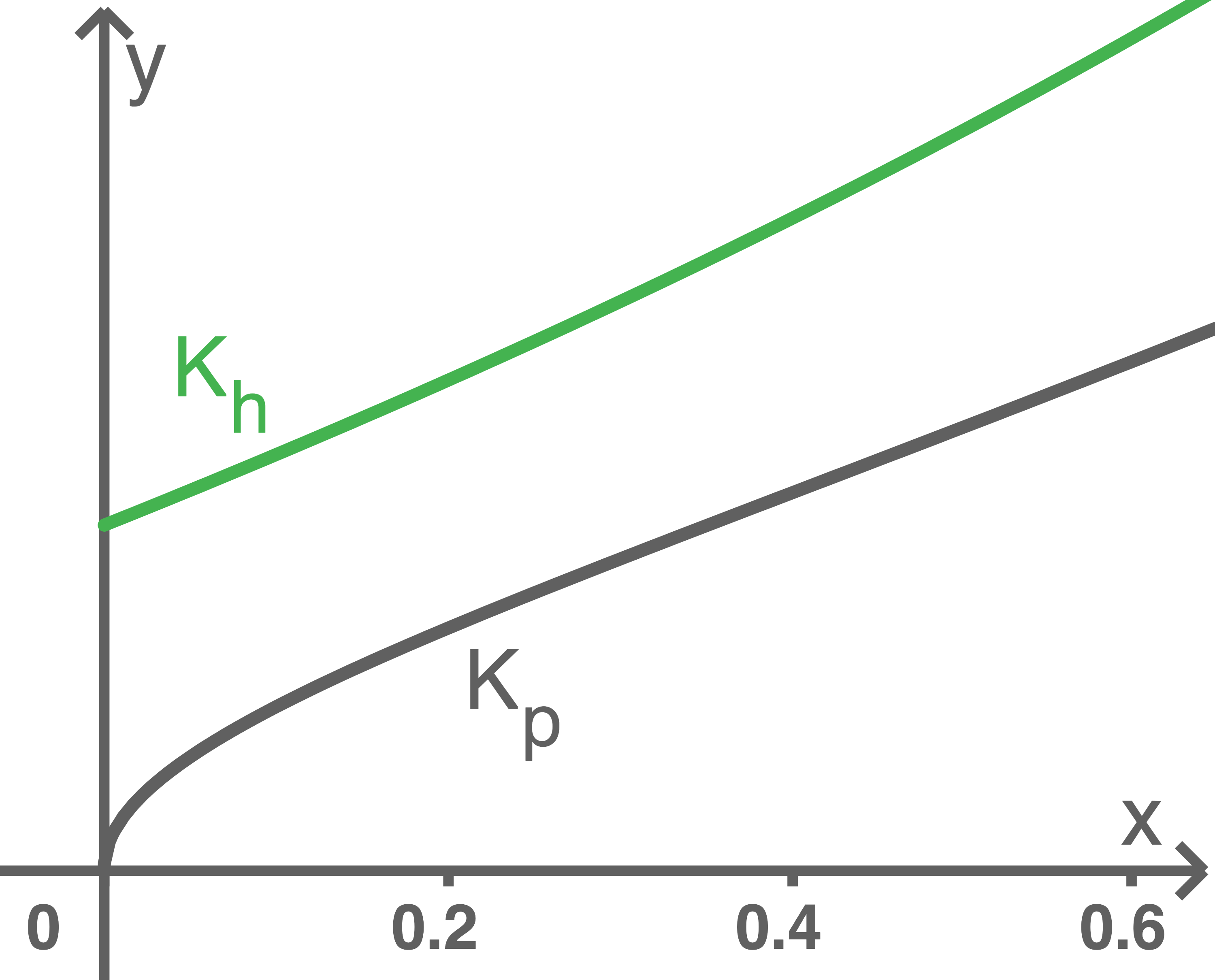
Die Abbildung zeigt jeweils einen Ausschnitt des Schaubilds  sowie des Schaubilds
sowie des Schaubilds  einer für
einer für  definierten Funktion
definierten Funktion 
Betrachtet wird der Term
Betrachtet wird der Term
1.2.3.1
Erläutere die Bedeutung des Wertes von  im dreidimensionalen geometrischen Zusammenhang.
im dreidimensionalen geometrischen Zusammenhang.
2
1.2.3.2
Es gilt:
![\(T=\pi \cdot\left[\frac{1}{2}\mathrm e^{2 x}+\frac{1}{3} x^3\right]_{0,2}^{0,4}.\)](https://mathjax.schullv.de/bb2a418c08792102bf634bdea31550aae89259c50b906082fff2a3850efc0d2b?color=5a5a5a) Ermittle einen Funktionsterm für
Ermittle einen Funktionsterm für 
3
20
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1.1
Symmetrie begründen
Bei  handelt es sich um eine ganzrationale Funktion vierten Grades, deren Funktionsterm nur gerade Exponenten enthält. Der Graph einer solchen Funktion ist symmetrisch zur
handelt es sich um eine ganzrationale Funktion vierten Grades, deren Funktionsterm nur gerade Exponenten enthält. Der Graph einer solchen Funktion ist symmetrisch zur  -Achse.
Umfang des Dreiecks bestimmen
1. Schritt: Koordinaten der Schnittpunkte mit der
-Achse.
Umfang des Dreiecks bestimmen
1. Schritt: Koordinaten der Schnittpunkte mit der  -Achse bestimmen
Da
-Achse bestimmen
Da  gilt folgt aufgrund der Symmetrie auch
gilt folgt aufgrund der Symmetrie auch 
 schneidet die
schneidet die  -Achse also in den Punkten
-Achse also in den Punkten  und
und  2. Schritt: Koordinaten des Schnittpunkts mit der
2. Schritt: Koordinaten des Schnittpunkts mit der  -Achse bestimmen
-Achse bestimmen

 schneidet die
schneidet die  -Achse in dem Punkt
-Achse in dem Punkt  3. Schritt: Umfang bestimmen
3. Schritt: Umfang bestimmen


 Der Umfang des Dreiecks beträgt also:
Der Umfang des Dreiecks beträgt also:
![\(U= 2 + \sqrt{5} + \sqrt{5} = 2+2\sqrt{5}\approx 6,47\,\text{[LE]}\)](https://mathjax.schullv.de/2ffe1b05c23aa1ed7f5a3c00730dcfd22e12cb3ead8cb2e0f20a0b6b8e9d7d7b?color=5a5a5a)
1.1.2
Für einen Wendepunkt muss das notwendige Kriterium  erfüllt sein.
erfüllt sein.

 Gleichsetzen liefert:
Gleichsetzen liefert:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/a3abe6befa3fe1d1032825cf17bd8e04e37070604ce0cc5b9e58ada4f9290907?color=5a5a5a) Da das Quadrat einer Zahl nicht negativ sein kann, besitzt die Gleichung
Da das Quadrat einer Zahl nicht negativ sein kann, besitzt die Gleichung  keine Lösung.
keine Lösung.  besitzt also keine Stelle, an der das notwendige Kriterium für Wendestellen erfüllt ist.
besitzt also keine Stelle, an der das notwendige Kriterium für Wendestellen erfüllt ist.  kann daher keinen Wendepunkt besitzen.
kann daher keinen Wendepunkt besitzen.
1.1.3
Flächeninhalt berechnen
Geradengleichung bestimmen
Aufgrund der Symmetrie liegt der Hochpunkt von  auf der
auf der  -Achse und hat somit die Koordinaten
-Achse und hat somit die Koordinaten 
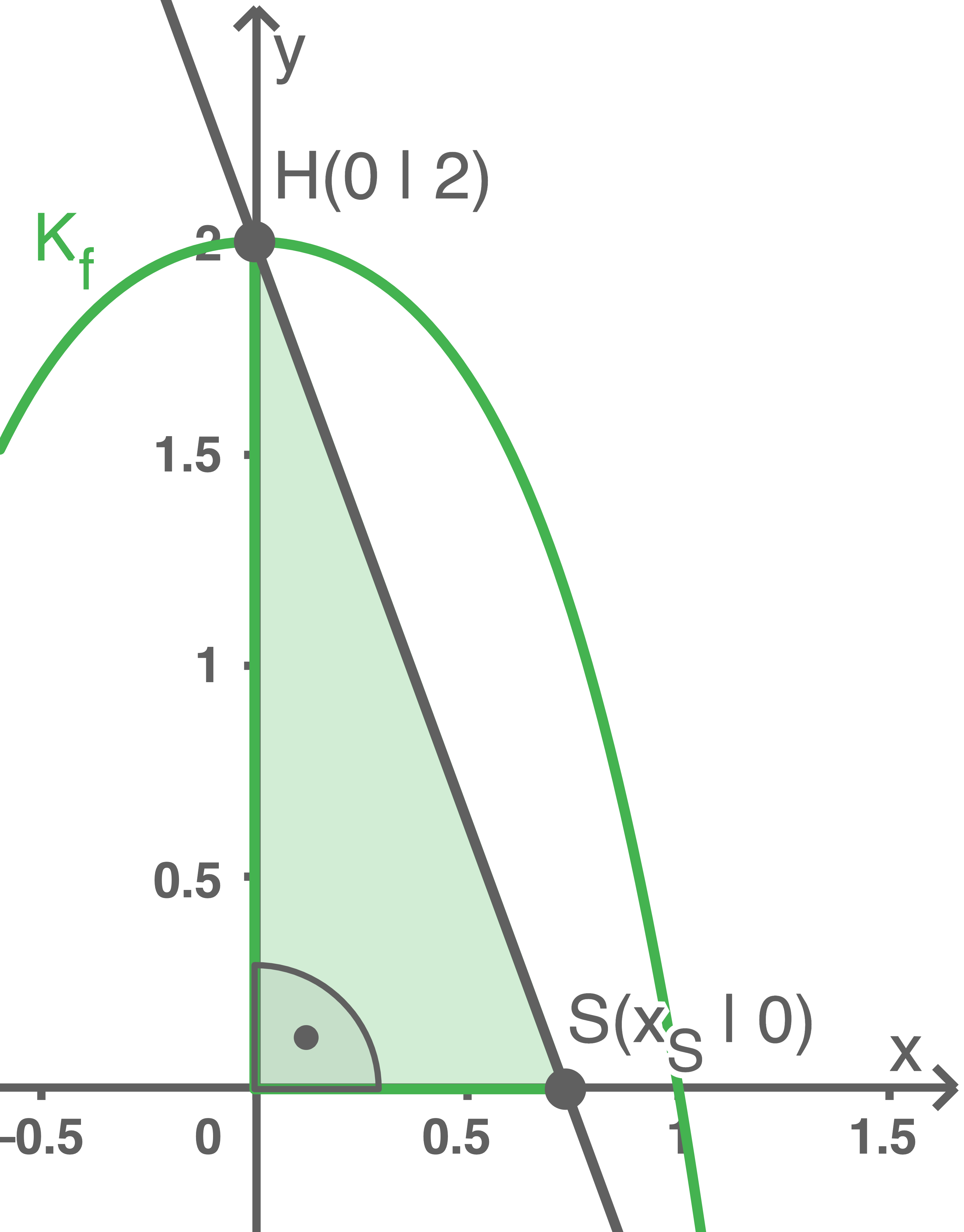 Dadurch ergibt sich folgende Gleichung für den Flächeninhalt des Dreiecks:
Dadurch ergibt sich folgende Gleichung für den Flächeninhalt des Dreiecks:
![\(\begin{array}[t]{rll}
A_{\text{Dreieck}} &=& \dfrac{1}{2}\cdot y_H \cdot x_S \\[5pt]
\dfrac{11}{15} &=& \dfrac{1}{2}\cdot 2 \cdot x_S \\[5pt]
\dfrac{11}{15} &=& x_S \\[5pt]
x_S &=& \dfrac{11}{15}
\end{array}\)](https://mathjax.schullv.de/be98902a6b6a53eb31e954a666d757b2feab42f788026a537e573e15daf4f530?color=5a5a5a) Die gesuchte Gerade schneidet die
Die gesuchte Gerade schneidet die  -Achse also im Punkt
-Achse also im Punkt  Die Steigung der Geraden folgt mit dem Differenzenquotienten:
Die Steigung der Geraden folgt mit dem Differenzenquotienten:
 Da die Gerade durch den Hochpunkt
Da die Gerade durch den Hochpunkt  verläuft, ist der
verläuft, ist der  -Achsenabschnitt
-Achsenabschnitt 
Eine Gleichung der Geraden lautet daher:
Die gesuchte Gerade bildet mit den Koordinatenachsen ein rechtwinkliges Dreieck mit dem Flächeninhalt
![\(A_{\text{Dreieck}} = \dfrac{A}{2} = \dfrac{ \frac{22}{15}}{2} = \dfrac{11}{15}\,\text{[FE]}.\)](https://mathjax.schullv.de/4c342deeca9741d95f605a25f862968044547d0638aced1fcb3c2a1e254cfbaa?color=5a5a5a)

Eine Gleichung der Geraden lautet daher:
1.2.1
Mit dem Intervallhalbierungsverfahren kann die Nullstelle von  näherungsweise bestimmt werden.
näherungsweise bestimmt werden.


 Die Nullstelle muss also im Intervall
Die Nullstelle muss also im Intervall ![\([-1;-0,5]\)](https://mathjax.schullv.de/e5f9e217c3e8a8edbc5e3ccbf871a1517afed3a9d8a0390b2671d31cc4abb5cf?color=5a5a5a) liegen.
liegen.

 Die Nullstelle muss also im Intervall
Die Nullstelle muss also im Intervall ![\([-0,75;-0,5]\)](https://mathjax.schullv.de/1d4afe49addd81231614468111a894cbc28f8bdbaf979aeb881dab20412ea71b?color=5a5a5a) liegen.
liegen.
 Die Nullstelle muss also im Intervall
Die Nullstelle muss also im Intervall ![\([-0,625;-0,5]\)](https://mathjax.schullv.de/84b1cd3c2318417c3ac21d775498d9be90eb291c684c1ca79573c237e715cb79?color=5a5a5a) liegen.
liegen.

 Die Nullstelle muss also im Intervall
Die Nullstelle muss also im Intervall ![\([-0,625;-0,5625]\)](https://mathjax.schullv.de/1710a740d646acac3d0e0d8899665328b57f5e116a16bdfea6a2cf869b84b92d?color=5a5a5a) liegen.
liegen.

 Die Nullstelle muss also im Intervall
Die Nullstelle muss also im Intervall ![\([-0,59375;-0,5625]\)](https://mathjax.schullv.de/6a73ca48f43668a5d6c00dc651ce5897924532274d96ca06ff2e99b3bb153745?color=5a5a5a) liegen.
liegen.

 Die Nullstelle muss also im Intervall
Die Nullstelle muss also im Intervall ![\([-0,578125;-0,5625]\)](https://mathjax.schullv.de/4073b8b5de9db14f32868abc10a5d68f62c452c0b6e0e33b9bad73de840c4597?color=5a5a5a) liegen.
liegen.

 Die Nullstelle muss also im Intervall
Die Nullstelle muss also im Intervall ![\([-0,5703125;-0,5625]\)](https://mathjax.schullv.de/3e9bcdbd46ddeeebab556eb98c332267e6a89d44b6ae40be7c28b5367d6d8466?color=5a5a5a) liegen.
liegen.

 Die Nullstelle muss also im Intervall
Die Nullstelle muss also im Intervall ![\([-0,5703125;-0,56640625]\)](https://mathjax.schullv.de/3380418d38d510e893f86fea3cc2926278a6f4dab768632c22cab184438c4e7d?color=5a5a5a) liegen.
liegen.


 Die Nullstelle muss also im Intervall
Die Nullstelle muss also im Intervall ![\([-0,568359375;-0,56640625]\)](https://mathjax.schullv.de/681522885c982c9bcb3990284542d17f051b5b1bc2b9b45389044fde8dcf1889?color=5a5a5a) liegen.
Beide Intervallgrenzen haben die gleichen ersten beiden Nachkommastellen. Für die gesuchte Nullstelle gilt also
liegen.
Beide Intervallgrenzen haben die gleichen ersten beiden Nachkommastellen. Für die gesuchte Nullstelle gilt also 
Da die dritten Nachkommastellen und
und  sind, ergibt das gerundet auf zwei Nachkommastellen
sind, ergibt das gerundet auf zwei Nachkommastellen 
Da die dritten Nachkommastellen
1.2.2
Damit die Gerade und  sich berühren, müssen sie in der Stelle, in der sie sich berühren, die gleiche Steigung und den gleichen Funktionswert haben.
Für die verschobene Gerade gilt
sich berühren, müssen sie in der Stelle, in der sie sich berühren, die gleiche Steigung und den gleichen Funktionswert haben.
Für die verschobene Gerade gilt  Sie hat an jeder Stelle die Steigung
Sie hat an jeder Stelle die Steigung  Die Steigung von
Die Steigung von  wird durch die erste Ableitungsfunktion von
wird durch die erste Ableitungsfunktion von  beschrieben:
beschrieben:
 Gleichsetzen mit
Gleichsetzen mit 
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/892f9b8f6c7f8c88c08fc681ebd784dda180e9410cb9edb00f2d51d32632f040?color=5a5a5a) An der Stelle
An der Stelle  haben die Gerade und
haben die Gerade und  also die gleiche Steigung.
also die gleiche Steigung.
 Die Gerade muss also so verschoben werden, dass ihr
Die Gerade muss also so verschoben werden, dass ihr  -Achsenabschnitt
-Achsenabschnitt  ist. Sie muss also um eine Längeneinheit nach oben verschoben werden.
ist. Sie muss also um eine Längeneinheit nach oben verschoben werden.
1.2.3.1
1.2.3.2
Der erste angegebene Term für  kann wie folgt umgeformt und zusammengefasst werden:
Der zweite gegebene Term kann wie folgt umgeformt werden:
kann wie folgt umgeformt und zusammengefasst werden:
Der zweite gegebene Term kann wie folgt umgeformt werden:
![\(\begin{array}[t]{rll}
T &=& \pi \cdot\left[\frac{1}{2}\mathrm e^{2 x}+\frac{1}{3} x^3\right]_{0,2}^{0,4} \\[5pt]
&=& \pi\cdot \displaystyle\int_{0,2}^{0,4}\left(\mathrm e^{2x}+x^2\right)\;\mathrm dx
\end{array}\)](https://mathjax.schullv.de/38aed4f6b370c19abb37e959662b4db1e8d540d0134581ecfcb28ba9085502a3?color=5a5a5a) Damit beide Terme identisch sind, muss folgendes gelten:
Damit beide Terme identisch sind, muss folgendes gelten: