Matrizen 2

In einem Gewächshaus einer Gärtnerei werden Blumen gezüchtet, deren Blüten die Farben rot $(R),$ violett $(V)$ oder blau $(B)$ haben.
Dabei können aus Samen von Blumen in der nächsten Generation auch Blumen einer anderen Farbe entstehen. Dieses Änderungsverhalten ist in der Tabelle dargestellt.

von nach	R	V	B
R	0,4	0,2	0
V	0,6	0,6	0,6
B	0	0,2	0,4

Beispielsweise bedeutet dies, dass aus dem Samen einer roten Blume mit einer Wahrscheinlichkeit von $40\,\%$ eine rote und mit einer Wahrscheinlichkeit von $60\,\%$ eine violette Blume in der nächsten Generation entsteht.

2.1

Die Gesamtzahl der Blumen bleibt von Generation zu Generation unverändert.

Nenne die Eigenschaft der zugehörigen Übergangsmatrix, die dies garantiert.
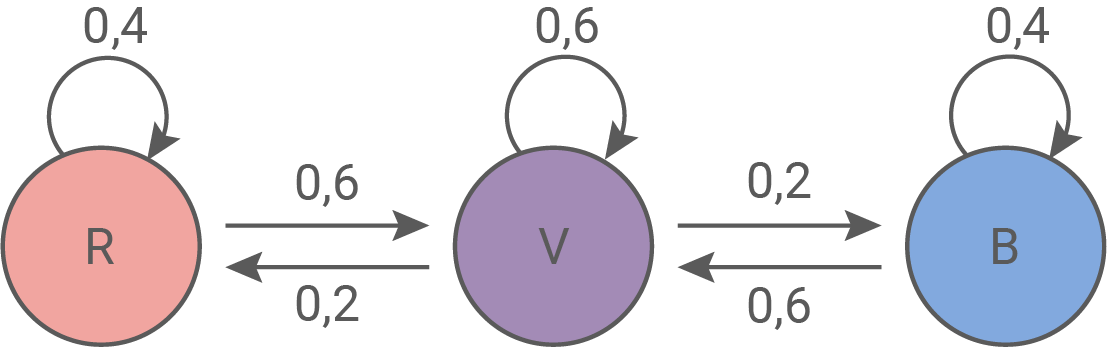
Zeichne das zugehorige Übergangsdiagramm.

2.2

Zu Beginn einer Beobachtung befinden sich 9000 Blumen im Gewächshaus, von denen 2000 rot und 6 mal so viele violett wie blau sind.

Berechne die zu erwartenden prozentualen Anteile von Blumen verschiedener Farben in der nächsten Generation.

2.3

Beurteile, ob die folgende Aussage wahr oder falsch ist:

„Stimmen die Anzahlen der Blumen der verschiedenen Farben in einer Generation überein, so ist deren Verhältnis in der nächsten Generation 1:3:1. In den folgenden Generationen ändert sich dann dieses Verhältnis nicht mehr."

2.4

Zu einem anderen Zeitpunkt befinden sich 1000 rote, 5400 violette und 2600 blaue Blumen im Gewächshaus.

Ermittle mit Hilfe des Modells jeweils die minimale und maximale Anzahl blauer Blumen der vorherigen Generation.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

2.1

Matrixeigenschaft nennen

Die Spaltensummen der zugehörigen Übergangsmatrix sind jeweils $1.$ Dadurch wird garantiert, dass in jeder Folgegeneration wieder gleich viele Blumen vorhanden sind.

Übergangsdiagramm zeichnen

Uebergangsdiagramm - Blumenfarben Baden-Württemberg Abi berufl. Gymnasium nichttechnisch

2.2

1. Schritt: Anzahl Blumen der verschiedenen Farben berechnen

Von insgesamt 9000 Blumen sind 2000 rot. Also sind 7000 violett oder blau. Da sechsmal so viele violett wie blau sind, gilt:

$\begin{array}[t]{rll} v + b &=& 7000 \\[5pt] 6b + b &=& 7000 &\quad \scriptsize \mid\; v= 6b \\[5pt] 7b &=& 7000 &\quad \scriptsize \mid\; :7 \\[5pt] b &=& 1000 \end{array}$

Also sind 1000 blaue und 6000 violette Blumen in der ersten Generation.

2. Schritt: Anzahl Blumen der nächsten Generation berechnen

Mit Hilfe der Übergangsmatrix

$M= \pmatrix{0,4 & 0,2 & 0 \\ 0,6 & 0,6 & 0,6 \\ 0 & 0,2 & 0,4}$

lässt sich die Verteilung der Blumen in der nächsten Generation berechnen:

Rechenweg anzeigen

$...=\pmatrix{2000\\5400 \\1600}$

3. Schritt: Prozentuale Anteile berechnen

Insgesamt gibt es 9000 Blumen.

$p_R=\dfrac{2000}{9000} = \dfrac{2}{9} \approx 22,2\,\%$

$p_V=\dfrac{5400}{9000} = 0,6 = 60\,\%$

$p_B=\dfrac{1600}{9000} = \dfrac{8}{45} = 17,8\,\%$

2.3

Stimmen die Anteile der Blumen in einer Generation überein, dann haben sie jeweils den Anteil $\frac{1}{3}.$ Für die folgende Generation ergibt sich dann:

Rechenweg anzeigen

$... = \pmatrix{\frac{1}{5}\\ \frac{3}{5} \\ \frac{1}{5}}$

Der erste Teil der Aussage stimmt also, da die Blumen in der Folgegeneration $\frac{1}{5}:\frac{3}{5}:\frac{1}{5}$ verteilt sind, was dem Verhältnis $1:3:1$ entspricht.

Rechenweg anzeigen

$= \pmatrix{\frac{1}{5}\\ \frac{3}{5} \\ \frac{1}{5}}$

Der zweite Teil der Aussage stimmt also auch. Die Aussage ist wahr.

2.4

Mit $r,$ $v$ und $b$ wird jeweils die Anzahl der roten, violetten und blauen Blumen in der vorherigen Generation bezeichnet. Damit gilt:

$\pmatrix{0,4 & 0,2 & 0 \\ 0,6 & 0,6 & 0,6 \\ 0 & 0,2 & 0,4} \cdot \pmatrix{r \\ v \\b} = \pmatrix{1000\\5400 \\2600}$

Daraus ergibt sich folgendes Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad& 0,4r +0,2 v &=& 1000 \\ \text{II}\quad& 0,6r +0,6v +0,6b &=& 5400 \\ \text{III}\quad& 0,2v +0,4b &=& 2600 \\ \end{array}$

Die Gleichungen werden so umgeformt, dass $r$ und $v$ in Abhängigkeit von $b$ dargestellt werden.

Aus $\text{III}$ folgt:

$\begin{array}[t]{rll} 0,2v +0,4b &=& 2600 &\quad \scriptsize \mid\; -0,4b \\[5pt] 0,2v &=& 2600 -0,4b &\quad \scriptsize \mid\; :0,2\\[5pt] v &=& 13000-2b \end{array}$

Einsetzen in $\text{I}:$

Rechenweg anzeigen

$r=-4000+b$

Die Gesamtanzahl der Blumen bleibt von Generation zu Generation gleich. In diesem Fall gibt es insgesamt $9000$ Blumen. Also muss gelten:

$0\leq r \leq 9000$ und $0\leq v \leq 9000$

Aus $0\leq r$ folgt:

$\begin{array}[t]{rll} 0 &\leq& r \\[5pt] 0 &\leq& -4000+b &\quad \scriptsize \mid\; +4000 \\[5pt] 4000 &\leq & b \end{array}$

Aus $r\leq 9000$ folgt:

$\begin{array}[t]{rll} r &\leq& 9000 \\[5pt] -4000+b &\leq& 9000 &\quad \scriptsize \mid\; +4000 \\[5pt] b &\leq & 13000 \end{array}$

Aus $0\leq v$ folgt:

$\begin{array}[t]{rll} 0 &\leq& v \\[5pt] 0 &\leq& 13000-2b &\quad \scriptsize \mid\; +2b \\[5pt] 2b &\leq & 13000 &\quad \scriptsize \mid\; :2\\[5pt] b &\leq& 6500 \end{array}$

Aus $v\leq 9000$ folgt:

$\begin{array}[t]{rll} v &\leq& 9000 \\[5pt] 13000-2b &\leq& 9000 &\quad \scriptsize \mid\; -13000 \\[5pt] -2b &\leq & -4000 &\quad \scriptsize \mid\; :(-2)\\[5pt] b &\geq& 2000 \end{array}$

Insgesamt ergibt sich damit $4000 \leq b \leq 6500.$

Für die vorherige Generation gilt also:

Die minimale Anzahl blauer Blumen beträgt $4000.$
Die maximale Anzahl blauber Blumen beträgt $6500.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?