Vektorgeometrie 1

In einem Museum gibt es einen quaderförmigen Raum, in dem ein Kunstwerk in Pyramidenform ausgestellt wird. Die Seitenflächen der Pyramide sind undurchsichtig. Im Modell liegt der Boden des Raums in einem Teil der $x_1x_2$ -Ebene mit $x_2 \geq 0.$
Die quadratische Grundfläche $ABCD$ der Pyramide hat die Eckpunkte $A(0 \mid 4 \mid 0)$ , $B(4 \mid 4\mid 0), C(4 \mid 8 \mid 0)$ und $D$ . Die Spitze $S$ der Pyramide liegt vier Längeneinheiten senkrecht über dem Schnittpunkt der beiden Diagonalen der Grundfläche. Eine Längeneinheit entspricht einem Meter $(\text{m})$ .

1.1

Begründe, dass die Spitze der Pyramide im Punkt $S (2 \mid 6 \mid 4)$ liegt.

1.2

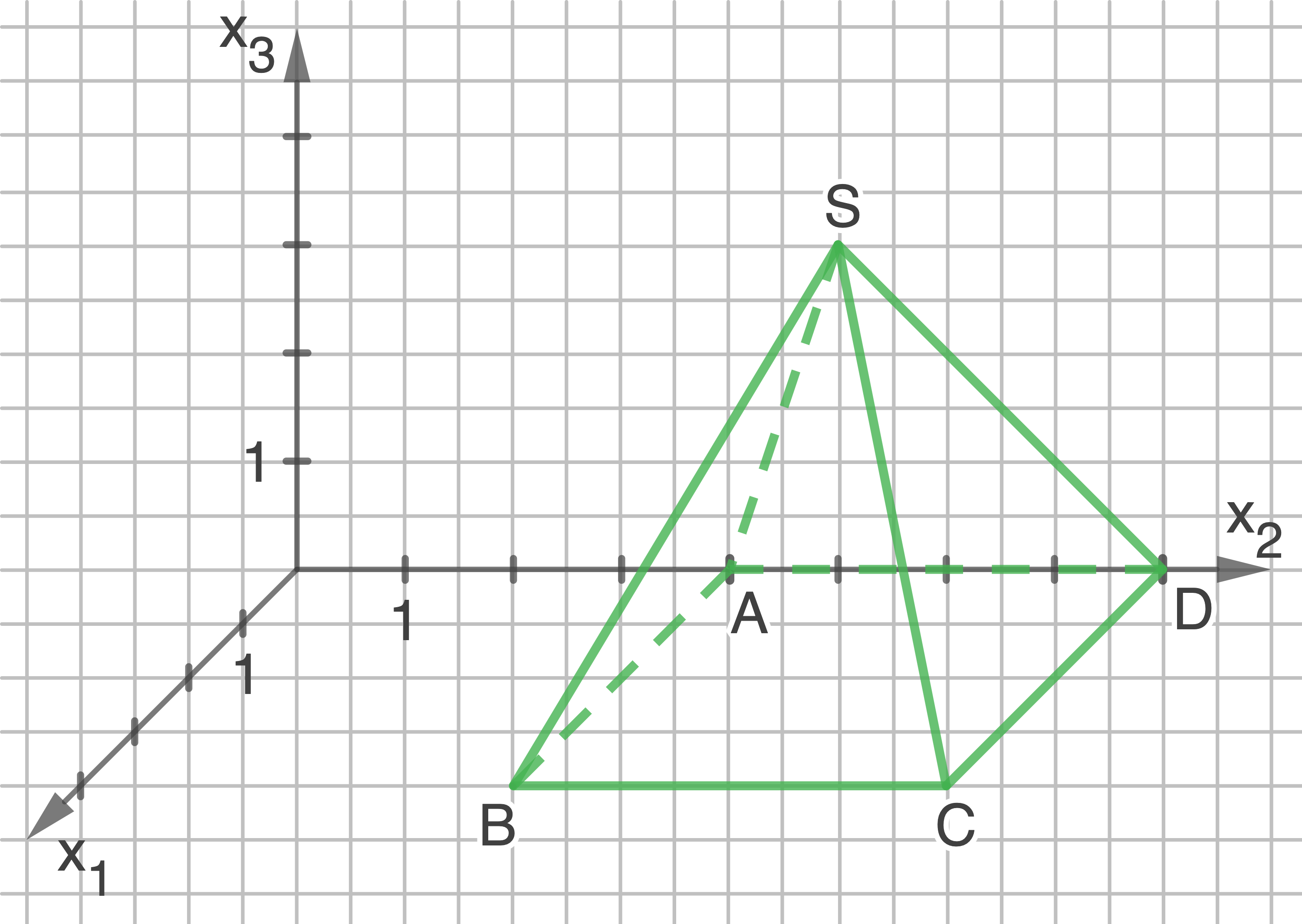
Zeichne die Pyramide in ein räumliches Koordinatensystem ein.

1.3

Die Seitenflächen der Pyramide werden mit einem Material beschichtet, das 1500 Euro pro Quadratmeter kostet.
Ermittle die Kosten dieser Beschichtung.

1.4

Der Raum wird nach einer Seite hin durch eine fensterlose Wand begrenzt, die Teil der $x_1x_3$ - Ebene mit $x_3 \geq 0$ ist. Die gegenüberliegende Wand besteht aus Glas.
Vormittags tritt Sonnenlicht durch die Glaswand ein. Das Sonnenlicht verläuft in Richtung des Vektors

$\overrightarrow{r} = \pmatrix{2\\-10\\-8}$

und verursacht einen Schatten der gesamten Pyramide.
Untersuche, ob dieser Schatten auf die fensterlose Wand trifft.

1.5

Im Punkt $K(0\mid 9 \mid 3)$ ist eine Überwachungskamera angebracht, wobei die Pyramide die Überwachung des gesamten Raums verhindert.
Ein punktförmiges Objekt bewegt sich vom Punkt $P(5 \mid 4 \mid 2)$ aus in Richtung des Vektors $\overrightarrow{AC}.$
Bestimme die Koordinaten des Punktes Q, an dem das Objekt von der Kamera erstmalig erfasst werden kann.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

$\overrightarrow{OS}$ $= \overrightarrow{0A} + \frac{1}{2}\cdot \overrightarrow{AC} + \pmatrix{0\\0\\4}$ $= \pmatrix{0\\4\\0} +\frac{1}{2}\cdot \pmatrix{4\\4\\0} + \pmatrix{0\\0\\4} = \pmatrix{2\\6\\4}$

1.2

Grafik eines dreidimensionalen Koordinatensystems mit einem grünen Pyramidenmodell und Punkten A, B, C, D, S.

1.3

Die Pyramide hat vier gleich große dreieckige Seitenflächen. Der Flächeninhalt des Dreiecks ADS ergibt sich zu

$A_{ADS}=\dfrac{1}{2} \cdot a \cdot h_a$ mit $a= \left| \overrightarrow{AD} \right|$ und $h_a= \left| \overrightarrow{MS} \right|.$

Dabei ist $M(0\mid 6 \mid 0)$ der Mittelpunkt der Strecke $\overline{AD}.$

Die Länge der Grundseite beträgt $a= \left| \overrightarrow{AD} \right| = 4 \,\text{FE}.$
Für die Höhe gilt:

$h_a= \left| \overrightarrow{MS} \right|= \left| \pmatrix{2\\0\\4} \right|$ $=\sqrt{2^2+0^2+4^2}$ $= 2 \sqrt{5}$

$A_{ADS}=\dfrac{1}{2} \cdot 4 \cdot 2 \sqrt{5} = 4 \sqrt{5}$

Für die Kosten folgt:

$4 \cdot 4 \sqrt{5} \cdot 1500 \approx 53.665,63\,[€]$

1.4

Der Schatten der Spitze ist ausschlaggebend.
Die Sonnenstrahlen, die auf die Spitze treffen können durch folgende Geradengleichung beschrieben werden:

$g: \overrightarrow{x} = \pmatrix{2\\6\\4} + r \cdot \pmatrix{2\\-10\\-8}$

Schneidet diese Gerade die $x_1x_3-$ Ebene im für $x_3$ positiven Bereich, so werden trifft der Schatten der Pyramide die Wand.
Für die $x_1x_3-$ Ebene gilt die Gleichung $x_2 =0.$
Für die Gerade der Sonnenstrahlen durch die Spitze gilt $x_2= 6-10r.$
Einsetzen liefert:

$\begin{array}[t]{rll} 0&=& 6-10r&\quad \scriptsize \mid\;+10r \\[5pt] 10r&=& 6&\quad \scriptsize \mid\;:10 \\[5pt] r &=& 0,6 \end{array}$

Der Schnittpunkt mit der $x_1x_3-$ Ebene ergibt sich zu

$S_1= \pmatrix{2\\6\\4} + 0,6 \cdot \pmatrix{2\\-10\\-8} = \pmatrix{3,2\\0\\-0,8}.$

Da sich der Schnittpunkt der Sonnengerade mit der $x_1x_3-$ Ebene im für $x_3$ negativen Bereich befindet, fällt der Schatten nicht auf die Wand, sondern nur auf den Boden, also auf die $x_1x_2$ -Ebene.

1.5

Das Sichtfeld der Kamera wird vor allem durch die Kante $\overline{SC}$ der Pyramide begrenzt. Betrachtet wird daher die Ebene $E_K$ mit den Punkten $K,$ $S$ und $C.$

Aus den Richtungsvektoren $\overrightarrow{KC}=\pmatrix{4\\-1\\-3}$ und $\overrightarrow{KS}=\pmatrix{2\\-3\\1}$ kann ein Normalenvektor der Ebene bestimmt werden.

$\overrightarrow{n_K}= \pmatrix{4\\-1\\-3} \times \pmatrix{2\\-3\\1}$ $=\pmatrix{-10\\-10\\-10} = -10\cdot \pmatrix{1\\1\\1}$

Eine Koordinatenform der Ebene $E_K$ ist folglich

$\begin{array}[t]{rll} x_1+x_2+x_3&=&c &\quad \scriptsize \mid\; \text{K einsetzen} \\[5pt] 0+9+3= 12 &=&c \\[5pt] \end{array}$

$K: x_1+x_2+x_3=12$

Die Flugbahn des Objektes kann mit folgender Gleichung beschrieben werden:

$\overrightarrow{AC} = \pmatrix{4\\4\\0}$ aufgestellt.

$g_P: \overrightarrow{x} = \overrightarrow{OP}+ s\cdot \overrightarrow{AC}$ $=\pmatrix{5\\4\\2} +s\cdot \pmatrix{4\\4\\0}$

Aus der Geradengleichung ergeben sich $x_1= 5+4s$ , $x_2= 4+4s$ und $x_3=2.$ Eingesetzt in die Ebenengleichung ergibt sich:

$\begin{array}[t]{rll} 5+4s+4+4s+2&=&12 \\[5pt] 11+8s &=&12 &\quad \scriptsize \mid\; -11\\[5pt] 8s &=&1 &\quad \scriptsize \mid\; :8\\[5pt] s&=&0,125 \end{array}$

Der Schnittpunkt zwischen Gerade und Ebene ergibt sich zu:

$\overrightarrow{OQ}= \pmatrix{5\\4\\2} +0,125\cdot \pmatrix{4\\4\\0} = \pmatrix{5,5\\4,5\\2}$

Ab dem Punkt $Q(5,5 \mid 4,5 \mid 2)$ kann das Objekt also von der Kamera erfasst werden.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?