Analysis

1.1

Die in $\mathbb{R}$ definierte Funktion $f$ ist gegeben durch $f(x)=2\cdot\mathrm{e}^x.$
Ordne die Werte

$f(0),$ $\(f$ und $\displaystyle\int_{0}^{1}f(x)\;\mathrm dx$

nach deren Größe in aufsteigender Reihenfolge.

1.2

Die Funktion $g$ ist gegeben durch $g(x)=x\cdot\sin(x);$ $-1\leq x \leq 10.$

Die Abbildung zeigt das Schaubild $K_g$ von $g.$

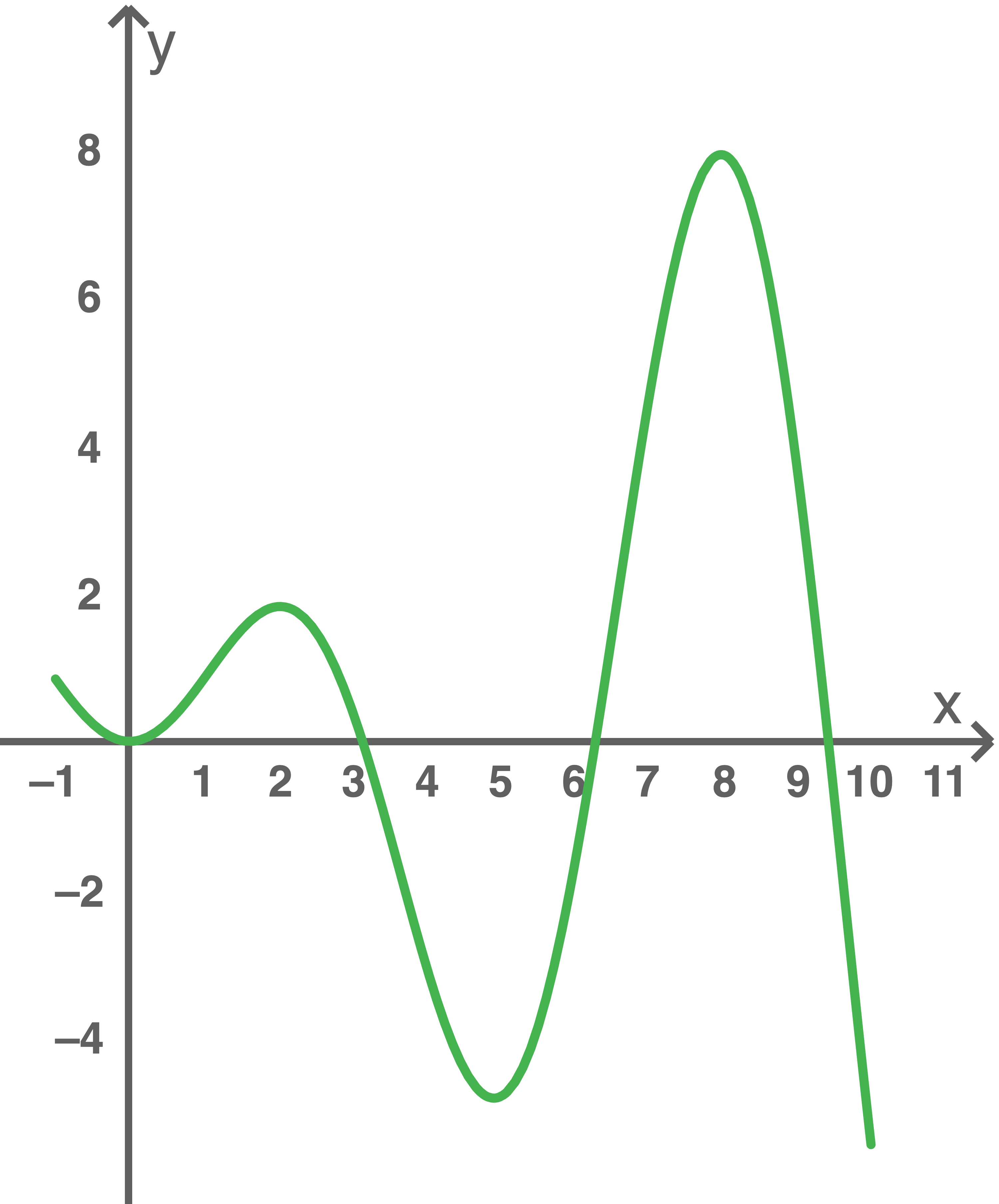
ba abi berufliches gymnasium technisch aufgabe 1 abbildung 1 funktion g

1.2.1

Bestimme die gemeinsamen Punkte von $K_g$ mit der ersten Winkelhalbierenden $y=x.$ Gib die Anzahl der Berührpunkte an.

1.2.2

Zeige dass die Funktion $G$ mit

$G(x)=-x\cdot\cos(x)+\sin(x);$ $-1\leq x\leq 10,$

eine Stammfunktion von $g$ ist.

Gib zudem die Stammfunktion von $g$ an, deren Schaubild den Punkt $(0\mid7)$ enthält.

1.3

Ermittle eine Gleichung der quadratischen Funktion $h,$ die die beiden folgenden Eigenschaften hat:

Der Graph von $h$ schneidet die Gerade mit der Gleichung $y=\dfrac{1}{4}x+1$ im Punkt $(0\mid1)$ unter einem rechten Winkel.
Die $x$ - und die $y$ -Koordinate des Extrempunkts des Graphen von $h$ stimmen überein.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

$f(0)= 2\cdot \mathrm e^0 = 2$

$\(f$ also $\(f$

$\begin{array}[t]{rll} \displaystyle\int_{0}^{1}f(x)\;\mathrm dx &=& \displaystyle\int_{0}^{1}2\cdot \mathrm e^x\;\mathrm dx \\[5pt] &=& [2\cdot \mathrm e^x]_0^1 \\[5pt] &=& 2\cdot \mathrm e - 2\\[5pt] &=& 2\cdot (\mathrm e-1) \\[5pt] \end{array}$

Es gilt $2\lt 2\cdot (\mathrm e -1) \lt 2\cdot \mathrm e.$

In aufsteigender Reihenfolge der Größe nach geordnet gilt also:

$f(0),$ $\,\displaystyle\int_{0}^{1}f(x)\;\mathrm dx,$ $\(\,f$

1.2.1

$\begin{array}[t]{rll} g(x) &=& y \\[5pt] x\cdot \sin(x) &=& x &\quad \scriptsize \mid\; -x\\[5pt] x\cdot \sin(x) -x &=& 0 \\[5pt] x\cdot \left(\sin(x) -1\right) &=& 0 \\[5pt] \end{array}$

Mit dem Satz vom Nullprodukt folgt, dass die Gleichung erfüllt ist, wenn mindestens einer der Faktoren $x$ oder $\sin(x)-1$ Null ist. Es folgt also als erste Lösung $x_1 = 0.$

Aus $\sin(x)-1 =0$ folgt $\sin(x)=1.$ Im betrachteten Bereich $-1\leq x \leq 10$ ist dies für $x_2 = \frac{1}{2}\pi$ und $x_3 = \frac{5}{2}\pi$ erfüllt.

Die Koordinaten der gemeinsamen Punkte von $K_g$ mit der ersten Winkelhalbierenden $y=x$ lauten $S_1(0\mid 0),$ $S_2\left( \frac{1}{2}\pi \,\bigg \vert \, \frac{1}{2}\pi\right)$ und $S_3\left( \frac{5}{2}\pi \,\bigg \vert \, \frac{5}{2}\pi\right).$

Wird die Winkelhalbierende in die Abbildung des Aufgabenblattes eingezeichnet, lässt sich erkennen, dass sie $K_g$ in $S_1$ schneidet und in $S_2$ und $S_3$ berührt.
Es gibt also zwei Berührpunkte.

1.2.2

Stammfunktion nachweisen

$G$ ist eine Stammfunktion von $g,$ wenn $\(G$ gilt. Mit der Produktregel folgt:

Rechenweg anzeigen

$\( G$

Stammfunktion mit Punkt angeben

$\begin{array}[t]{rll} G_c(0) &=& 7 \\[5pt] -0\cdot \cos(0) + \sin(0) + c &=& 7 \\[5pt] c &=& 7 \end{array}$

Das Schaubild der Stammfunktion $G_7$ mit $G_7(x)= -x\cdot \cos(x) + \sin(x) + 7$ von $g$ enthält den Punkt $(0\mid 7).$

1.3

Der Funktionsterm von $h$ hat die Form:

$h(x)= a\cdot x^2 +b\cdot x +c$

1. Bedingung anwenden

$\begin{array}[t]{rll} h(0) &=& 1 \\[5pt] a\cdot 0^2 +b\cdot 0 +c &=& 1 \\[5pt] c &=& 1 \end{array}$

Zusätzlich ist angegeben, dass der Graph von $h$ die Gerade mit der Gleichung $y= \frac{1}{4}x +1$ an der Stelle $x=0$ im rechten Winkel schneidet.

Die Steigung der Gerade lässt sich aus dem Funktionsterm ablesen und beträgt $m= \frac{1}{4}.$
Die Steigung des Graphen von $h$ muss an der Stelle $x=0$ also $\(h$ betragen.

Für die erste Ableitung von $h$ gilt:

$\(h$

$\(\begin{array}[t]{rll} h$

2. Bedingung anwenden

Wegen des notwendigen Kriteriums für Extremstellen gilt für die Extremstelle $x_E$ von $h:$

$\(\begin{array}[t]{rll} h$

Anmerkung: Da es sich bei $a=0$ nicht um eine quadratische Funktion handeln würde, ist $a\neq 0,$ sodass durch $a$ geteilt werden darf.

Es soll $h(x_E)=x_E$ gelten.

$\begin{array}[t]{rll} h(x_E) &=& x_E \\[5pt] a\cdot x_E^2 -4\cdot x_E + 1 &=& x_E &\quad \scriptsize \mid\;x_E=\frac{2}{a} \\[5pt] a\cdot \left(\frac{2}{a}\right)^2 -4\cdot \frac{2}{a} + 1 &=& \frac{2}{a} \\[5pt] \frac{4}{a}- \frac{8}{a} +1 &=& \frac{2}{a} \\[5pt] -\frac{4}{a}+1 &=& \frac{2}{a} &\quad \scriptsize \mid\;+\frac{4}{a} \\[5pt] 1 &=& \frac{6}{a} &\quad \scriptsize \mid\; \cdot a \\[5pt] a &=& 6 \end{array}$

$h(x)= 6x^2 -4x +1$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?