Analysis
1.1
Die Funktion 
ist gegeben durch 
; 
Das Schaubild von ist 
1.1.1
Bestimme die Nullstellen von und skizziere 
ohne weitere Rechnung.
4
1.1.2
Ermittle die x-Koordinate des Punktes, in dem die Steigung 
hat.
2
1.2
Die Abbildung zeigt einen Ausschnitt des Schaubildes einer Funktion 
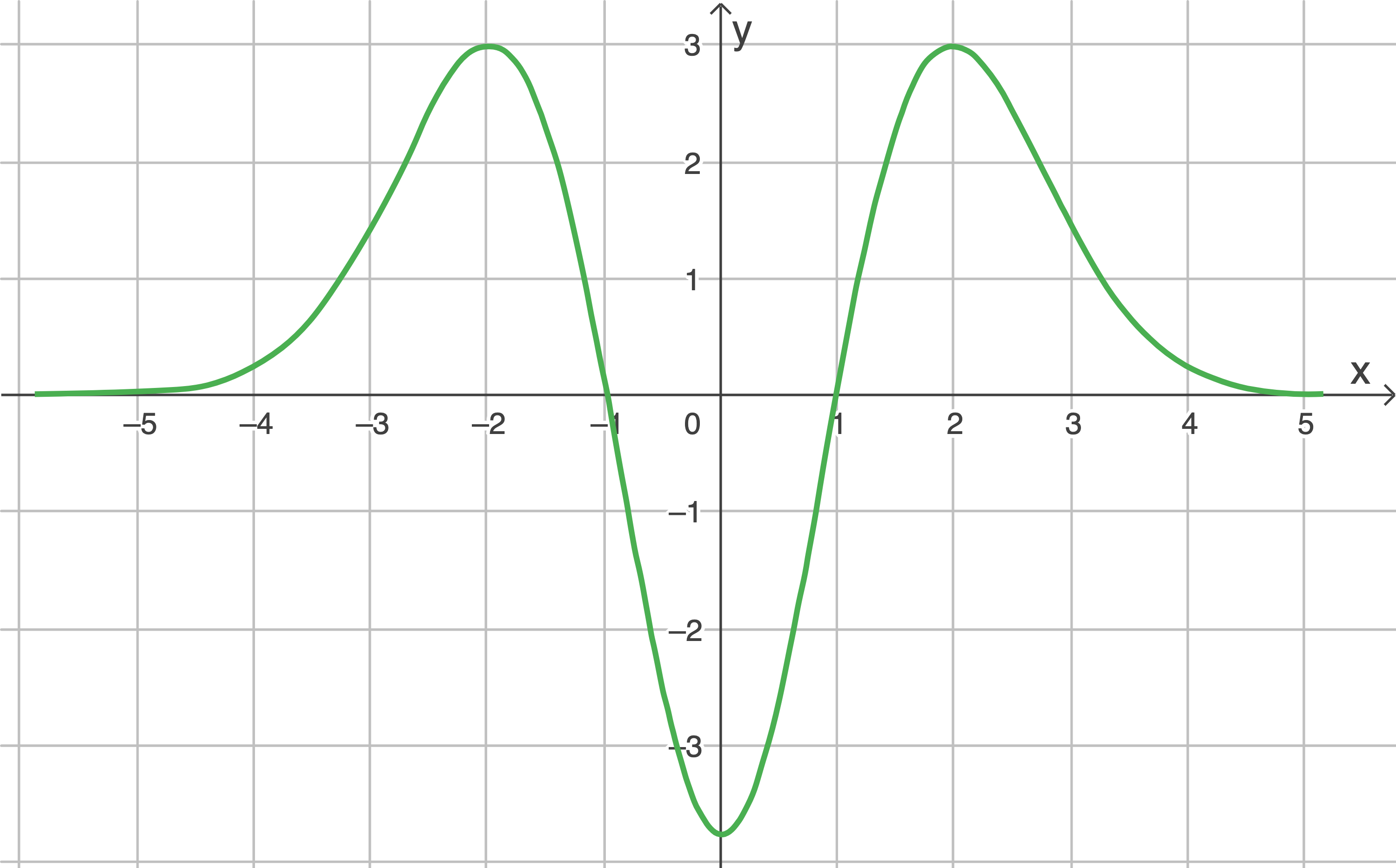Entscheide, ob die folgenden Aussagen wahr oder falsch sind. Begründe.
(1) Es gilt: 
(2) Das Schaubild der Ableitungsfunktion 
von 
besitzt für 
einen Hochpunkt.
(3) Der Wert von 
ist größer als 
5
1.3
Die Funktion 
ist für 
gegeben durch 
und 
ist eine Stammfunktion von 
Zeige: (1) ist für monoton wachsend.
(2) Die Stelle 
ist die einzige Wendestelle von 
Zeige: (1)
4
15
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1.1
Nullstellen
![\(\begin{array}[t]{rll}
f(x) &=& 0 \\[5pt]
-\dfrac{1}{2} x^3 + \dfrac{3}{2} x^2 &=& 0 \\[5pt]
\left(-\dfrac{1}{2} x + \dfrac{3}{2}\right)\cdot x^2 &=& 0
\end{array}\)](https://mathjax.schullv.de/6f452e4ed23347077a74649ee5626d245527db3f4c66a4e3413346b27e5f1b2b?color=5a5a5a)
Mit dem Satz vom Nullprodukt folgt 
oder
![\(\begin{array}[t]{rll}
-\dfrac{1}{2} x + \dfrac{3}{2} &=& 0 &\quad \scriptsize \mid\;+\dfrac{1}{2} x \\[5pt]
\dfrac{3}{2} &=& \dfrac{1}{2} x &\quad \scriptsize \mid\;\cdot 2 \\[5pt]
3 &=& x
\end{array}\)](https://mathjax.schullv.de/3bbb3301409304a0ee7859ce12efe593174927bcce5aa58cde54dd8b0bf3150b?color=5a5a5a)
Die Nullstellen von lauten 
und 
Skizze
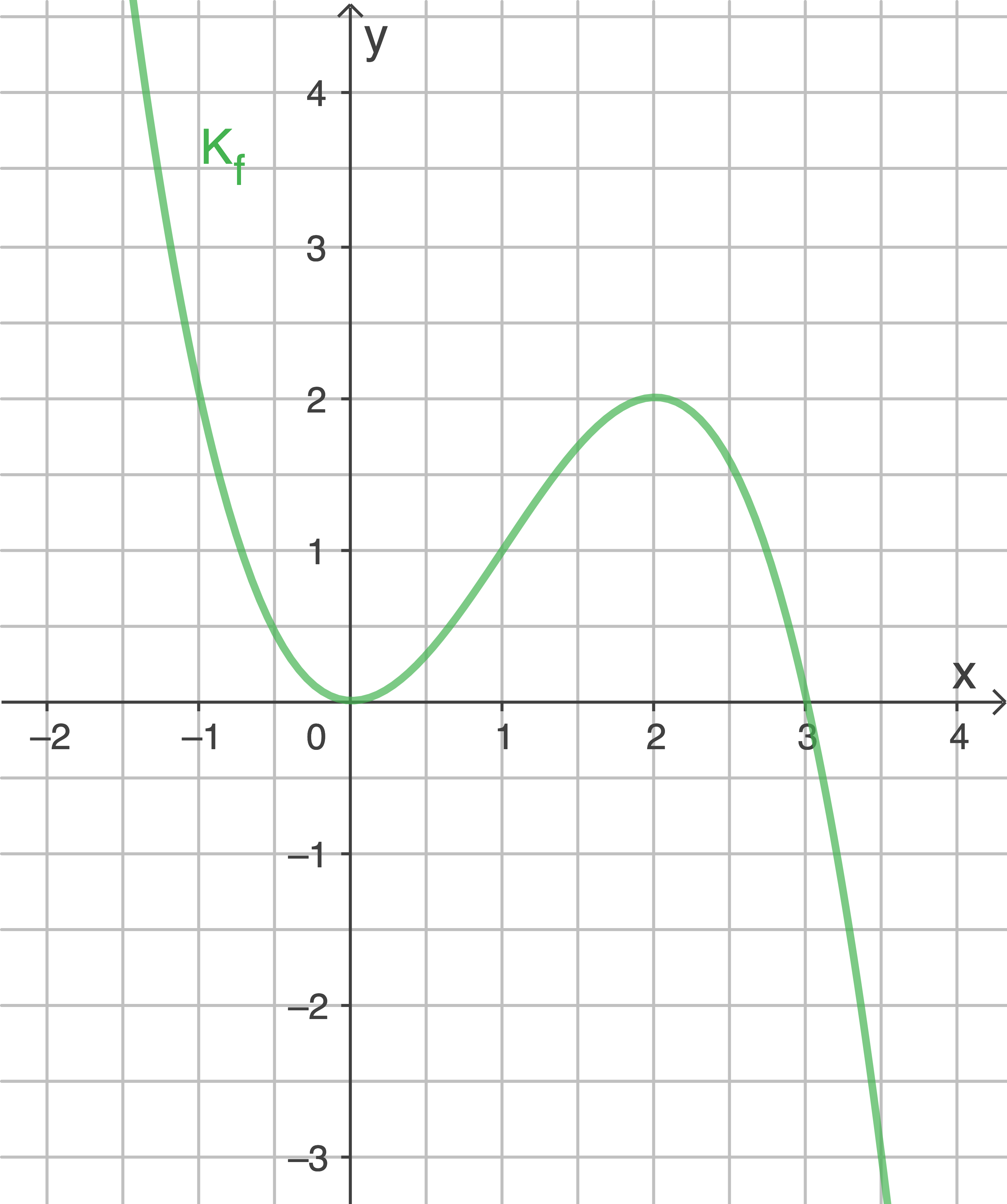
1.1.2
Die Steigung in einem Punkt wird durch die erste Ableitung von beschrieben.
Die 
-Koordinate des Punkts, in dem die Steigung 
hat lautet 
1.2
Aussage (1) ist falsch, da der Graph von in dem Bereich um 
herum linksgekrümmt ist und deshalb 
gelten muss.
Aussage (2) ist wahr. Es gilt 
und 
Für 
steigt der Graph von aber an, sodass in diesem Bereich einen positiven Wert annehmen und anschließend wieder fallen muss um bei 
wieder den Wert Null annehmen zu können.
Die Aussage (3) ist wahr, da der Graph von im Intervall ![\([0;4]\)](https://mathjax.schullv.de/1560f98ba45b1bf50e4254268fc3492c704d99f31b7a236afb4a70174b7d628e?color=5a5a5a)
zwei Teilflächen mit der -Achse begrenzt. Die kleinere der beiden Teilflächen liegt unterhalb der -Achse, die größere oberhalb, sodass der Wert des angegebenen Integrals insgesamt positiv ist.
1.3
(1)
Wenn 
gilt, dann ist streng monoton wachsend.
Für 
ist 
und somit ist die Funktion für monoton wachsend.
(2)
Es gilt:
![\(\begin{array}[t]{rll}
D](https://mathjax.schullv.de/601f53854f57e02aed240b23d750e8c880fccc2110d59056605089be2eff4ac2?color=5a5a5a)
1. Notwendiges Kriterium für Wendestellen
![\(\begin{array}[t]{rll}
D](https://mathjax.schullv.de/46e1d698a78ad7b7b589a0b3232575bb2e0f2da08e4ce6732bb1218952f71092?color=5a5a5a)
Für 
ergeben sich 
und 
Da nur betrachtet wird, fällt 
weg.
2. Hinreichendes Kriterium für Wendestellen
Für gilt
Somit ist die einzige Wendestelle von für 