Matrizen 2
2
Drei verschiedene Fitnessketten  ,
,  und
und  konkurrieren in einer Region um die insgesamt 10 000 Kunden. Die Kunden sind entweder ohne Vertrag oder sie sind als Mitglied bei genau einer Fitnesskette für ein Jahr angemeldet.
Jedes Jahr melden sich einige Kunden ohne Vertrag neu an, manche Mitglieder wechseln die Fitnesskette, manche bleiben bei ihrer Fitnesskette, einige scheiden aus und sind dann ohne Vertrag. Die Entwicklung von einem Jahr zum nächsten lässt sich modellhaft durch die Gleichung
konkurrieren in einer Region um die insgesamt 10 000 Kunden. Die Kunden sind entweder ohne Vertrag oder sie sind als Mitglied bei genau einer Fitnesskette für ein Jahr angemeldet.
Jedes Jahr melden sich einige Kunden ohne Vertrag neu an, manche Mitglieder wechseln die Fitnesskette, manche bleiben bei ihrer Fitnesskette, einige scheiden aus und sind dann ohne Vertrag. Die Entwicklung von einem Jahr zum nächsten lässt sich modellhaft durch die Gleichung  mit
mit
 und
und  beschreiben. Hierbei wird die Anzahl der Mitglieder der Fitnessketten ebenfalls mit
beschreiben. Hierbei wird die Anzahl der Mitglieder der Fitnessketten ebenfalls mit  ,
,  und
und  bezeichnet.
bezeichnet.  ist die Anzahl der Kunden ohne Vertrag.
ist die Anzahl der Kunden ohne Vertrag.
2.1
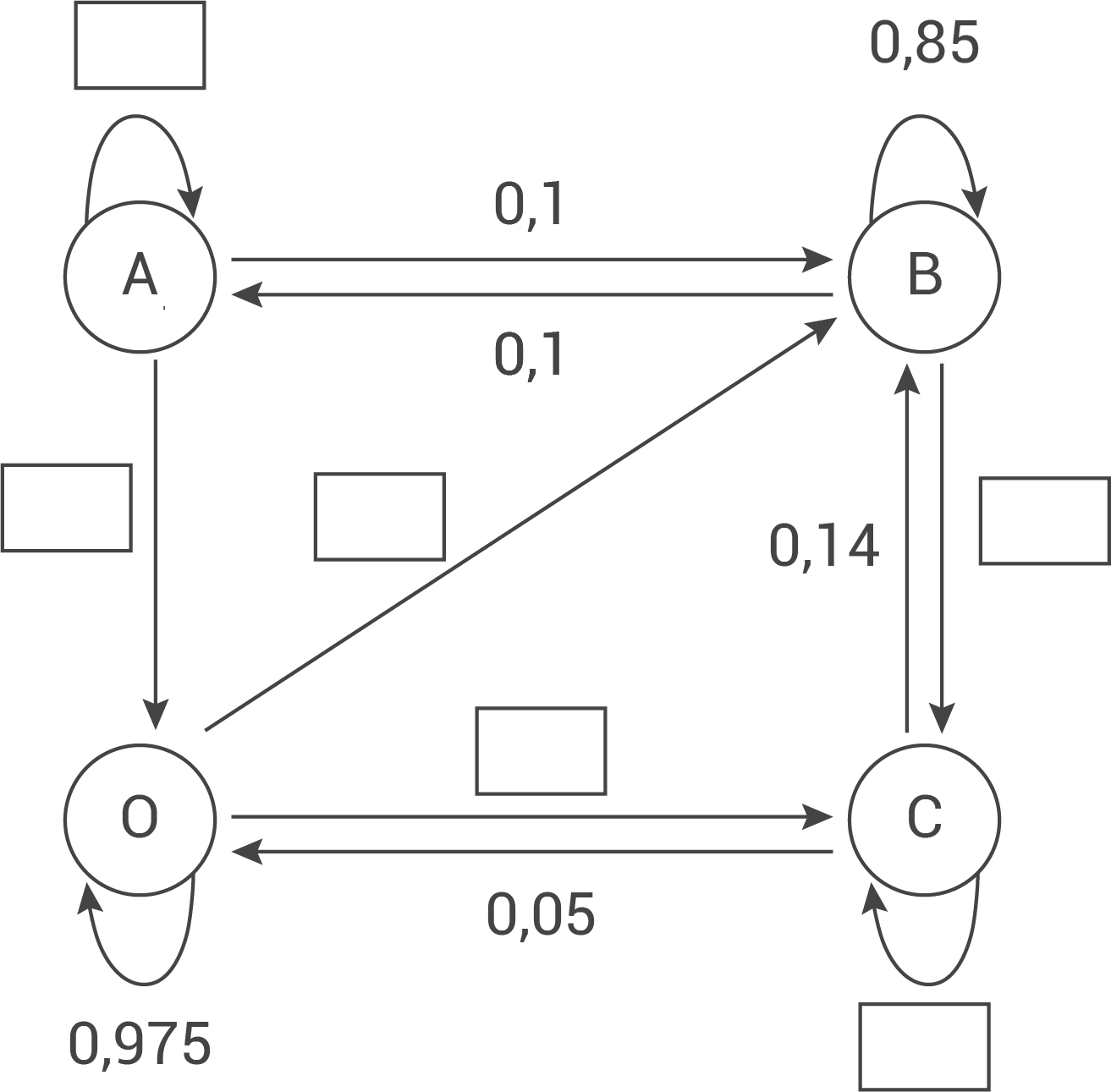
Vervollständige den Übergangsgraphen.

3
2.2
Interpretiere den Eintrag  im Sachzusammenhang.
Nenne die Fitnesskette, zu der ausschließlich Kunden kommen, die schon zuvor bei einer Kette angemeldet waren.
im Sachzusammenhang.
Nenne die Fitnesskette, zu der ausschließlich Kunden kommen, die schon zuvor bei einer Kette angemeldet waren.
2
2.3
Im Jahr 2020 waren jeweils 1400 Mitglieder in den drei Ketten angemeldet. Bestimme die Anzahl der Mitglieder der drei Ketten im Jahr 2021.
3
2.4
Langfristig werden 10 % der Kunden bei der Fitnesskette A angemeldet sein und 60 % der Kunden ohne Vertrag bleiben.
Ermittle die Verteilung aller Kunden, die von einem Jahr auf das nächste unverändert bleibt.
3
2.5
In einem Jahr hat die Fitnesskette  die doppelte Anzahl von Mitgliedern, wie jede der beiden anderen Ketten. Außerdem hat die Fitnesskette
die doppelte Anzahl von Mitgliedern, wie jede der beiden anderen Ketten. Außerdem hat die Fitnesskette  dann ein Jahr später 950 Mitglieder.
Ermittle die prozentuale Zunahme der Kunden ohne Vertrag.
dann ein Jahr später 950 Mitglieder.
Ermittle die prozentuale Zunahme der Kunden ohne Vertrag.
4
15
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
2.1
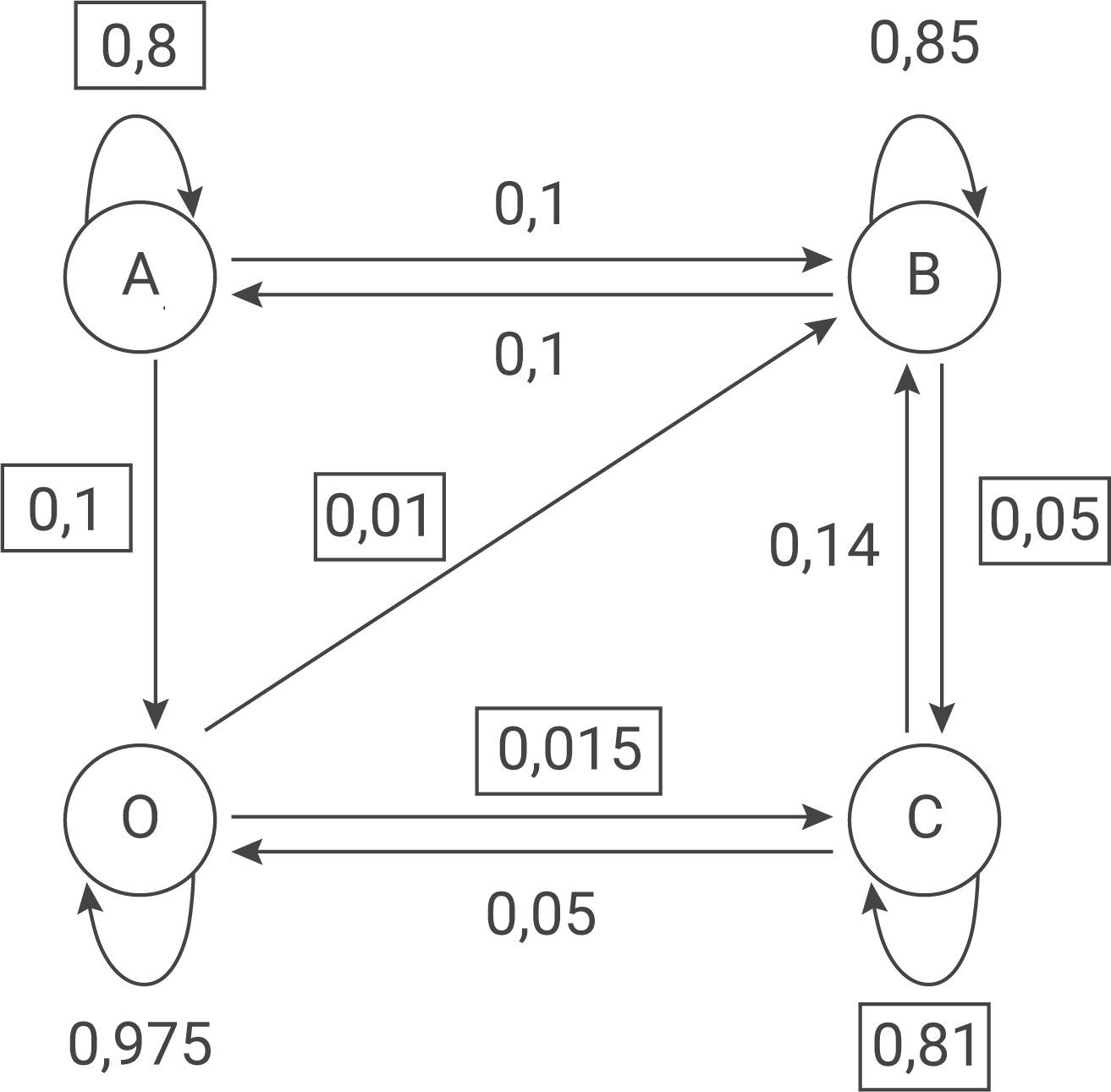
2.2
Jedes Jahr wechseln im Schnitt 14 % der Kunden von Fitnesskette C zur Fitnesskette B.
Zu Fitnesskette A kommen nur Kunden, die schon zuvor bei einer Kette angemeldet waren.
2.3
Da bei jeder der drei Fitnessketten jeweils 1.400 Kunden angemeldet waren, waren  Kunden ohne Vertrag.
Kunden ohne Vertrag.
Es ergibt sich: Im Jahr 2021 sind 1.260 Kunden bei Kette A, 1.584 Kunden bei Kette B und 1.291 Kunden bei Kette C angemeldet, sowie 5.865 ohne Vertrag.
Es ergibt sich: Im Jahr 2021 sind 1.260 Kunden bei Kette A, 1.584 Kunden bei Kette B und 1.291 Kunden bei Kette C angemeldet, sowie 5.865 ohne Vertrag.
2.4
Werden die dauerhaften Anteile der Kunden der verschiedenen Fitnessketten, bzw. ohne Vertrag mit 

 und
und  bezeichnet, dann gilt
bezeichnet, dann gilt  und
und 
Daraus ergibt sich folgende Gleichung:
 Aus der ersten Zeile folgt:
Da die Summe insgesamt 100 % ergeben muss,ergibt sich für
Aus der ersten Zeile folgt:
Da die Summe insgesamt 100 % ergeben muss,ergibt sich für 





 Bei der Verteilung der Kunden, die von einam Jahr auf das nächste unverändert bleibt, sind 10 % der Kunden bei Kette A, 20 % bei Kette B und 10 % bei Kette C angemeldet, sowie 60 % ohne Vertrag.
Bei der Verteilung der Kunden, die von einam Jahr auf das nächste unverändert bleibt, sind 10 % der Kunden bei Kette A, 20 % bei Kette B und 10 % bei Kette C angemeldet, sowie 60 % ohne Vertrag.
Daraus ergibt sich folgende Gleichung:
2.5
Es ergibt sich folgende Gleichung:
Aus der dritten Zeile der Matrixmultiplikation folgt:
Einsetzen von  und ausführen der Matrixmultiplikation ergibt dann:
Die Anzahl der Kunden ohne Vertrag ist also von 6.000 auf 6.100 angestiegen. Für die prozentuale Zunahme bedeutet das:
und ausführen der Matrixmultiplikation ergibt dann:
Die Anzahl der Kunden ohne Vertrag ist also von 6.000 auf 6.100 angestiegen. Für die prozentuale Zunahme bedeutet das:
