Stochastik 1
1
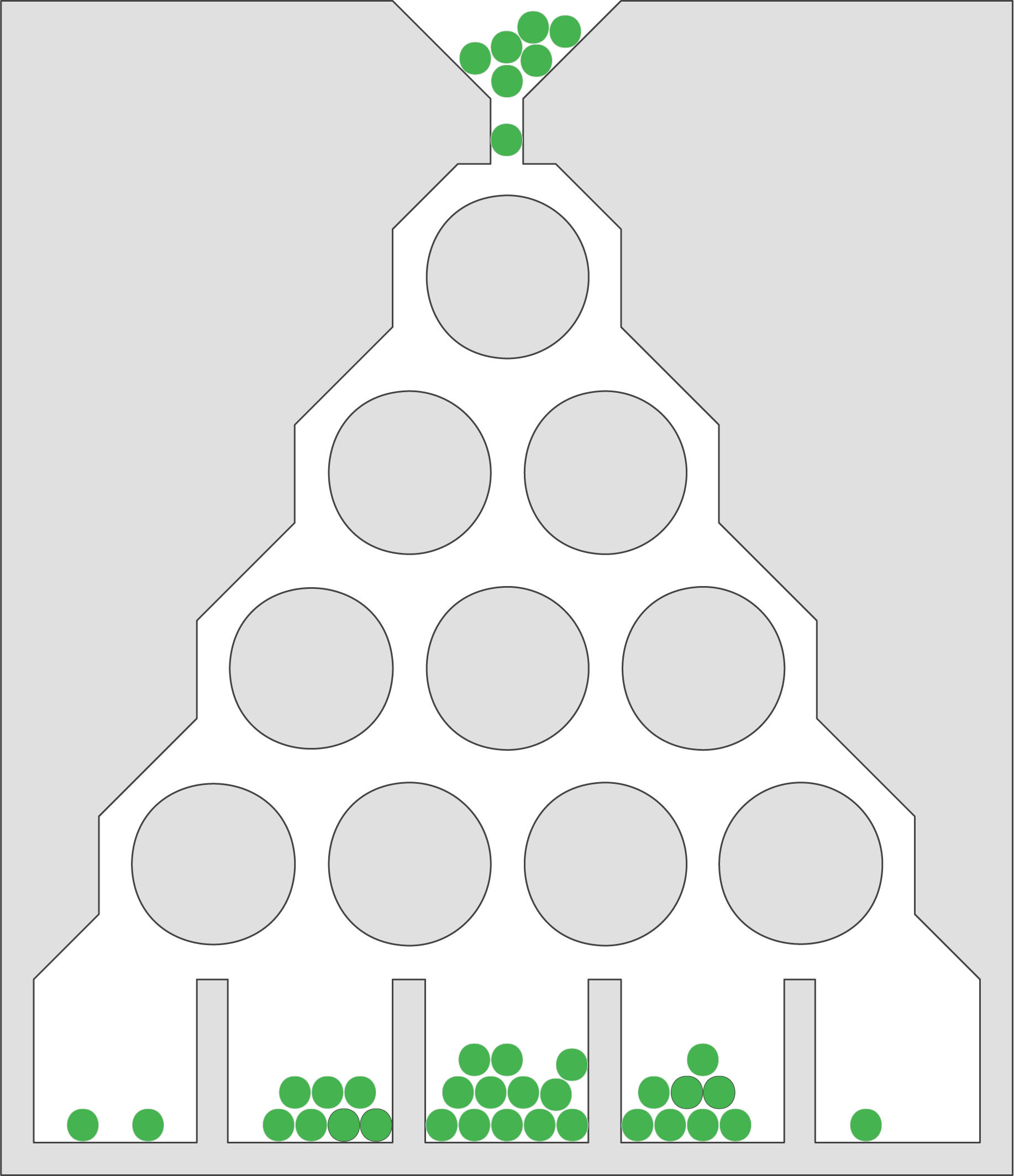
Eine Firma stellt Holzspielzeuge her. Abb. 1 illustriert die Funktionsweise eines sogenannten Galton-Bretts.
Bei diesem Spielzeug werden Kugeln von oben in einen Schacht gegeben und diese prallen dann auf runde Stifte, die sie jeweils entweder links oder rechts passieren, bevor sie in einem der unteren Fächer aufgefangen werden. Das in Abb. 1 dargestellte Galton-Brett hat die Länge vier, da jede Kugel an vier Stiften abprallt, bevor sie in einem der fünf Fächer landet. Ist ein ideales Galton-Brett waagrecht aufgestellt, so prallt jede Kugel von jedem Stift mit einer Wahrscheinlichkeit von 0,5 nach jeweils einer der beiden Seiten ab.
Bei diesem Spielzeug werden Kugeln von oben in einen Schacht gegeben und diese prallen dann auf runde Stifte, die sie jeweils entweder links oder rechts passieren, bevor sie in einem der unteren Fächer aufgefangen werden. Das in Abb. 1 dargestellte Galton-Brett hat die Länge vier, da jede Kugel an vier Stiften abprallt, bevor sie in einem der fünf Fächer landet. Ist ein ideales Galton-Brett waagrecht aufgestellt, so prallt jede Kugel von jedem Stift mit einer Wahrscheinlichkeit von 0,5 nach jeweils einer der beiden Seiten ab.
1.1
Eine Kugel wird in das Galton-Brett gegeben.
1.1.1
Erläutere, warum der Pfad der Kugel durch eine Bernoulli-Kette beschrieben werden kann.
Definiere in diesem Zusammenhang eine binomialverteilte Zufallsvariable
und gib die möglichen Werte von für ein Galton-Brett der Länge vier an.
Definiere in diesem Zusammenhang eine binomialverteilte Zufallsvariable
4
1.1.2
Berechne für ein Galton-Brett der Länge vier jeweils die Wahrscheinlichkeit der folgenden Ereignisse:
A: Die Kugel landet in einem der beiden Fächer rechts vom mittleren Fach.
B: Die Kugel landet nicht in einem der beiden äußeren Fächer.
B: Die Kugel landet nicht in einem der beiden äußeren Fächer.
4
1.2
Erfahrungsgemäß fallen 5 % der produzierten Galton-Bretter bei der Qualitätskontrolle durch. Diese werden als mangelhaft bezeichnet.
Prüfe, ob folgende Aussage wahr oder falsch ist:
„Mindestens 46 Galton-Bretter müssen überprüft werden, um mit einer Wahrscheinlichkeit von mehr als 90 % mindestens ein mangelhaftes Brett zu finden.“
„Mindestens 46 Galton-Bretter müssen überprüft werden, um mit einer Wahrscheinlichkeit von mehr als 90 % mindestens ein mangelhaftes Brett zu finden.“
3
1.3
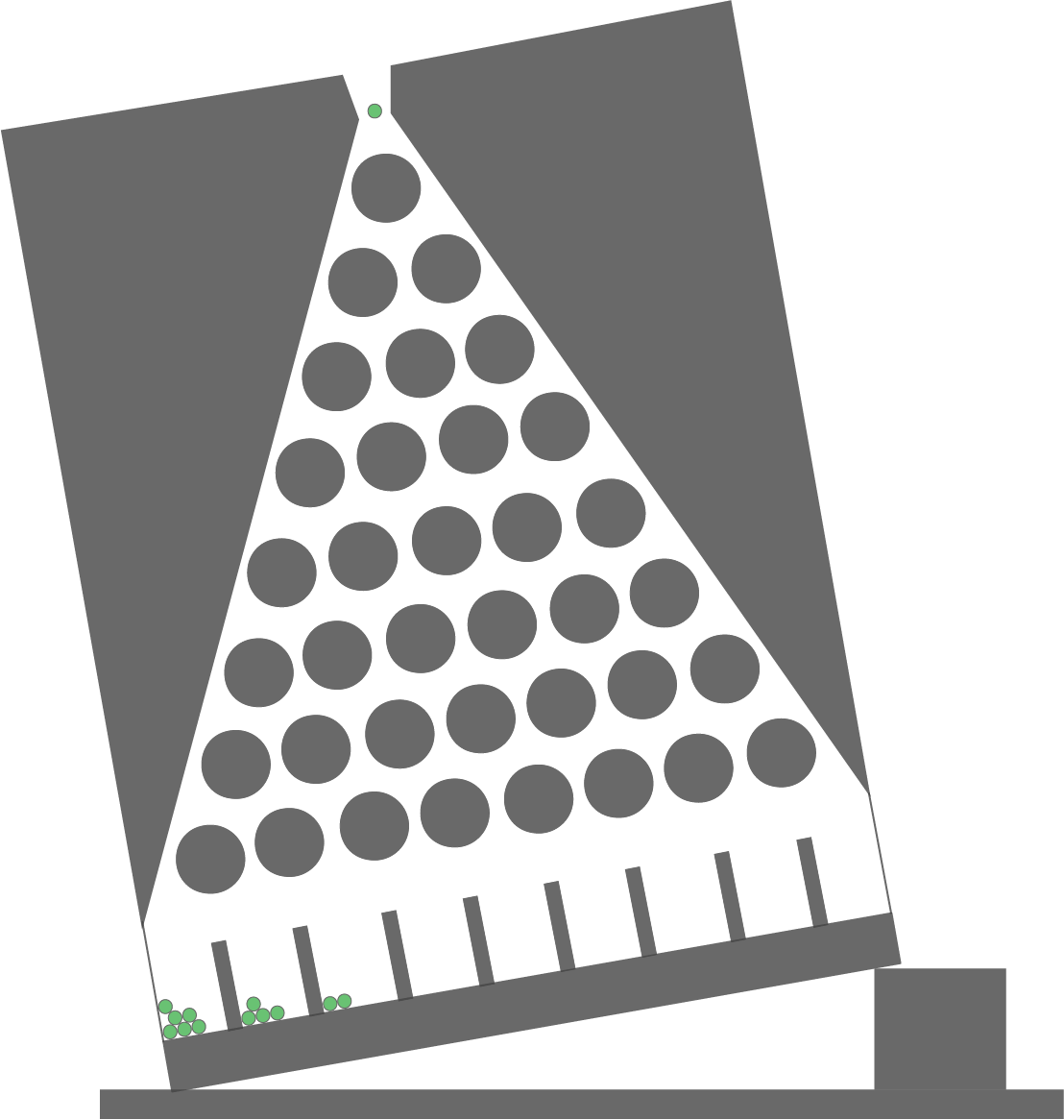
Jemand stellt ein Galton-Brett der Länge acht schräg auf (vgl. Abb. 2). Die Schrägstellung ist so, dass die Wahrscheinlichkeit, dass eine Kugel im mittleren Fach landet, den Wert 0,1 hat.
Eine Kugel wird in das Galton-Brett gegeben.
Ermittle die Wahrscheinlichkeit, dass die Kugel an den Stiften nach links abprallt.
Eine Kugel wird in das Galton-Brett gegeben.
Ermittle die Wahrscheinlichkeit, dass die Kugel an den Stiften nach links abprallt.
4
15
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.1.1
Bei der Funktionsweise des Galton-Bretts handelt es sich um eine Kette von stochastisch unabhängigen Bernoulli-Experimenten. Bei jedem Experiment gibt es zwei mögliche Ergebnisse mit der jeweiligen Wahrscheinlichkeit von 0,5, die sich nicht verändert. Deshalb kann der Pfad der Kugel durch eine Bernoulli-Kette beschrieben werden.
Die Zufallsvariable beschreibt die Anzahl der Abpraller nach rechts. Bei einem Galton-Brett der Länge vier kann die Werte 
und 
annehmen und ist binomialverteilt mit 
und 
1.1.2
Ereignis 
tritt ein, wenn die Kugel drei oder vier mal nach rechts abprallt.
Ereignis 
tritt ein, wenn die Kugel nicht null- oder viermal nach rechts abprallt.
1.2
Mit 
wird die Anzahl der Bretter bezeichnet
Für 
gilt 
Für 
gilt 
Es genügt also bereits 45 Bretter zu überprüfen, um darunter mit einer Wahrscheinlichkeit von mindestens 90 % mindestens ein mangelhaftes Brett zu finden.
Somit ist die Aussage falsch.
Somit ist die Aussage falsch.
1.3
Die Schrägstellung des Bretts beeinflusst die Trefferwahrscheinlichkeit 
dass die Kugel nach links abprallt. Wenn die Kugel im mittleren Fach landet, ist sie vier mal nach links abgeprallt. Es gilt:
Mit der 
Formel ergibt sich 
und 
Es kommt nur 
in Frage, da 
ist aufgrund der Schrägstellung.
Die Kugel prallt an den Stiften also mit einer Wahrscheinlichkeit von ca. 73,6 % nach links ab.
Die Kugel prallt an den Stiften also mit einer Wahrscheinlichkeit von ca. 73,6 % nach links ab.