Pflichtaufgaben
1 Analysis
Gegeben ist eine im Intervall![\([-4; 4]\)](https://www.schullv.de/resources/formulas/45030092f707f37f6d181387a8976f993fc2ab4591e710ff193d5590d81f3fa3_light.svg)
definierte Polynomfunktion 
vom Grad 
Der Graph von
ist punktsymmetrisch zum Ursprung und schneidet die 
-Achse im Punkt 
Der Wertebereich von
ist ![\(W_f = [-2; 2].\)](https://www.schullv.de/resources/formulas/39fa24c176bca1736e0dfd7fdcf5d6dbe7cff1e940ba344cdb4d1c70c5f6fdda_light.svg)
a)
Skizziere den Graphen der Funktion , wenn bekannt ist, dass 
gilt.
, wenn bekannt ist, dass gilt.
(3 BE)
b)
Bestimme eine Funktionsgleichung einer trigonometrischen Funktion 
, sodass und im Intervall dieselben Nullstellen haben.
, sodass und im Intervall dieselben Nullstellen haben.
(2 BE)
2 Analysis
Gegeben ist die in
definierte Funktion mit 
a)
Gib eine Gleichung der Asymptote des Graphen von an.
an.
(1 BE)
b)
Bestimme den -Wert, an dem der Graph von die Steigung 
hat.
-Wert, an dem der Graph von die Steigung hat.
(2 BE)
c)
Zeige, dass der Graph von keinen Wendepunkt hat.
keinen Wendepunkt hat.
(2 BE)
3 Stochastik
Eine Urne enthält 15 weiße und 15 rote Kugeln. Aus dieser wird 16-mal mit Zurücklegen gezogen.Die Zufallsgröße
gibt die Anzahl der gezogenen weißen Kugeln an.
Die Abbildung zeigt die Wahrscheinlichkeitsverteilung von
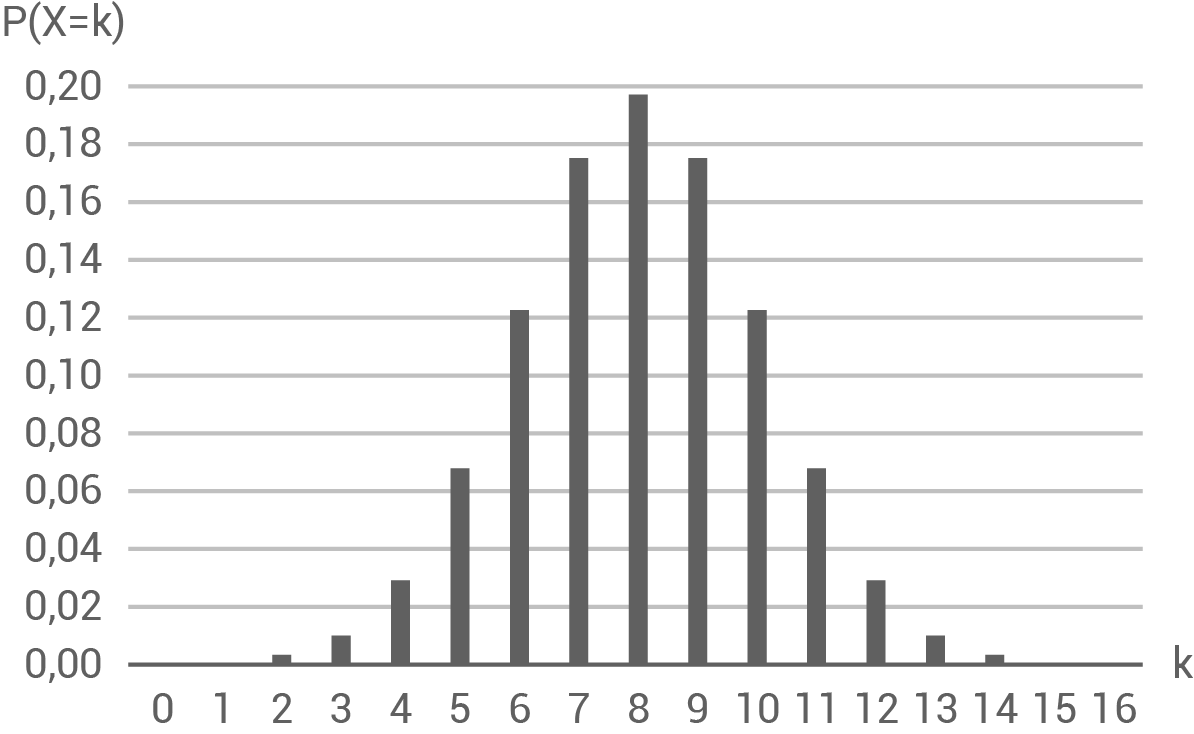
a)
Gib den Erwartungswert von an.
an.
(1 BE)
b)
Bestimme mit Hilfe von Werten aus der Abbildung näherungsweise die Wahrscheinlichkeit 
(2 BE)
c)
Die Zufallsgröße 
gibt die Anzahl der gezogenen roten Kugeln an.
Erläutere, warum die Wahrscheinlichkeitsverteilung von ebenfalls durch die Abbildung oben dargestellt werden kann.
gibt die Anzahl der gezogenen roten Kugeln an.
Erläutere, warum die Wahrscheinlichkeitsverteilung von ebenfalls durch die Abbildung oben dargestellt werden kann.
(2 BE)
4 Lineare Algebra
Gegeben sind die Punkte
, 
, 
und 
a)
Weise folgende Sachverhalte nach:
(1)
Der Punkt 
ist der Mittelpunkt der Strecke 
ist der Mittelpunkt der Strecke
(2)
Die Vektoren 
und 
schließen einen rechten Winkel ein.
und schließen einen rechten Winkel ein.
(2 BE)
b)
Bestimme die Koordinaten eines Punktes, der doppelt so weit vom Punkt entfernt ist wie vom Punkt 
entfernt ist wie vom Punkt
(3 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?1 Analysis
a)
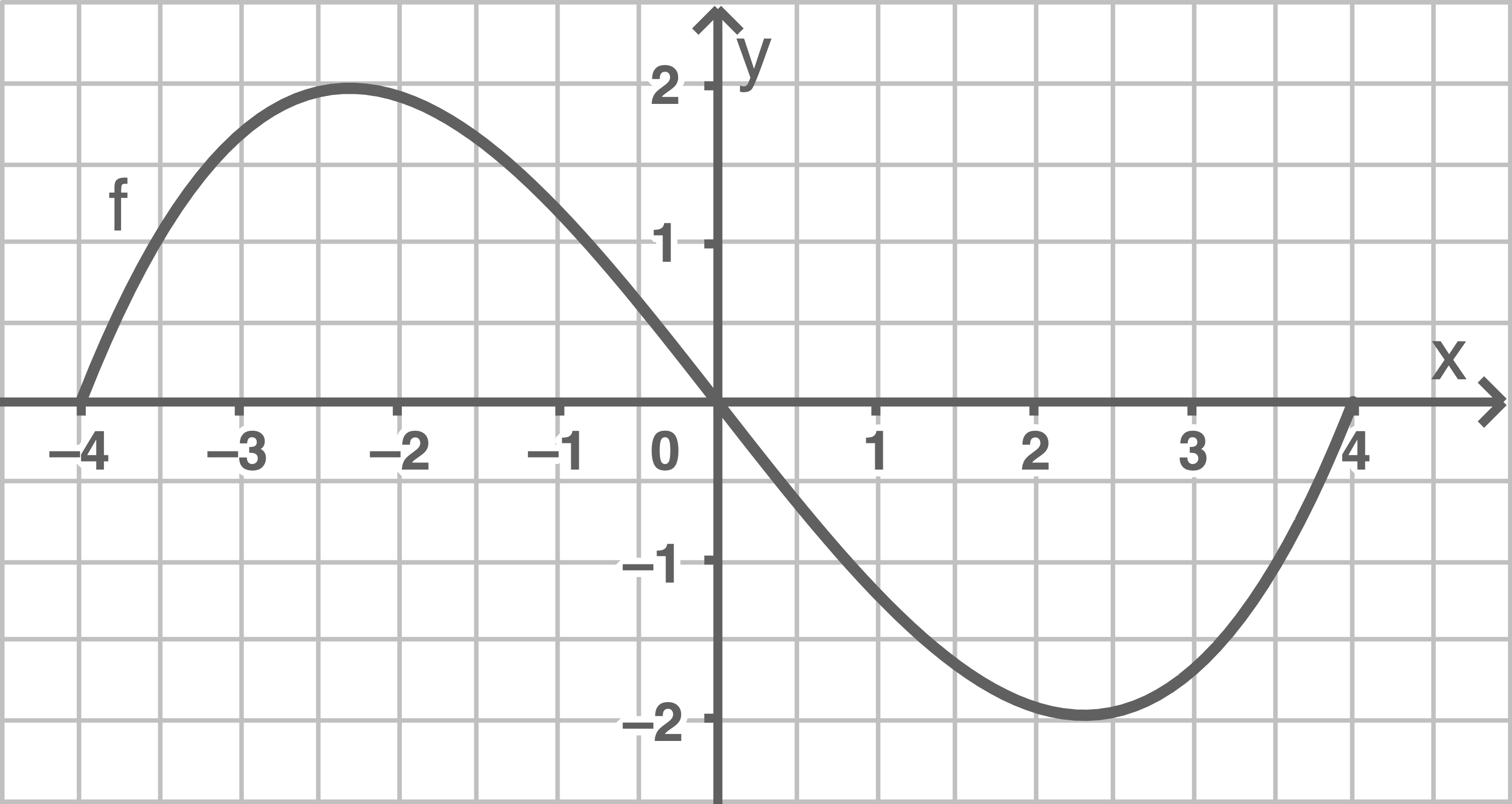
b)
Eine mögliche Funktionsgleichung mit denselben Nullstellen wie lautet 
lautet
2 Analysis
a)
b)
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/24360bc783624a500a9fdccd2bb327d8a97e44b377bc9730293636d12b5296d2_light.svg)
c)
Notwendige Bedingung für Wendestellen anwenden:
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/4ba0d3472ec2bc3fbb455b1163536e83a0a8b8849e5c6942b9fe71014eae1a0d_light.svg)
Wegen 
für alle 
ist die notwendige Bedingung für kein erfüllt und der Graph von hat folglich keinen Wendepunkt.
Wegen für alle ist die notwendige Bedingung für kein erfüllt und der Graph von hat folglich keinen Wendepunkt.
3 Stochastik
a)
Aus der Abbildung lässt sich direkt der Erwartungswert 
ablesen.
ablesen.
b)
Näherungweise gilt:
Daraus folgt:
![\(\begin{array}[t]{rll}
P(6\leq X \leq 7)&=& P(X=6)+P(X=7) \\[5pt]
&\approx& 0,12+0,175 \\[5pt]
&=& 0,295 \\[5pt]
&=& 29,5\,\%
\end{array}\)](https://www.schullv.de/resources/formulas/d860b0addf9098657618cd93c083bc8c72574e1060de7410fc88f628e3a61231_light.svg)
Daraus folgt:
c)
Die Urne enthält genauso viele weiße wie schwarze Kugeln. Daher ist die Wahrscheinlichkeitsverteilung von und gleich und kann durch die gleiche Abbildung dargestellt werden.
und gleich und kann durch die gleiche Abbildung dargestellt werden.
4 Lineare Algebra
a)
(1)
![\(\begin{array}[t]{rll}
\overrightarrow{OA}+\dfrac{1}{2}\overrightarrow{AB}&=& \pmatrix{1\\3\\3}+\dfrac{1}{2}\pmatrix{9-1\\-1-3\\-5-3} \\[5pt]
&=& \pmatrix{1\\3\\3}+\dfrac{1}{2}\pmatrix{8\\-4\\-8} \\[5pt]
&=& \pmatrix{5\\1\\-1}
\end{array}\)](https://www.schullv.de/resources/formulas/157b6ead4664091d08e59cd3ab5721c08ffc66ec0676271a9b7786312c1d063b_light.svg)
Die Koordinaten des Mittelpunkts der Strecke 
sind folglich gegeben durch 
(2)
Damit stehen die beiden Vektoren senkrecht aufeinander und schließen folglich einen rechten Winkel ein.
![\(\begin{array}[t]{rll}
\overrightarrow{AM}\circ \overrightarrow{MC}&=& \pmatrix{5-1\\1-3\\-1-3}\circ\pmatrix{3-5\\5-1\\-5-(-1)}\\[5pt]
&=& \pmatrix{4\\-2\\-4}\circ\pmatrix{-2\\4\\-4}\\[5pt]
&=& 4\cdot (-2)+(-2)\cdot 4+(-4)\cdot (-4) \\[5pt]
&=& 0
\end{array}\)](https://www.schullv.de/resources/formulas/ed2e78311884cb93c7d906f8e707abc13db652921053f1d886aff86429caf9ad_light.svg)
b)
Der Punkt mit den Koordianten 
ist doppelt so weit vom Punkt entfernt wie vom Punkt
ist doppelt so weit vom Punkt entfernt wie vom Punkt