Lerninhalte in Mathe

Abi-Aufgaben GK (GTR)

Abi-Aufgaben GK (CAS)

Digitales Schulbuch

Inhaltsverzeichnis

Aufgabe 3

Aufgabenstellung

In einem kartesischen Koordinatensystem sind die Punkte $O( 0 \mid 0 \mid 0 )$ , $A( 8 \mid 0 \mid 0 )$ , $B( 8 \mid 8 \mid 0 )$ , $C (0 \mid 8 \mid 0)$ , $D( 8 \mid 0 \mid 8 )$ , $E( 8 \mid 8 \mid 8 )$ , $F( 0 \mid 8 \mid 8 )$ und $G( 0 \mid 0 \mid 8 )$ Eckpunkte eines Würfels $OABCDEFG$ . Außerdem sind die Punkte $L (8 \mid 0 \mid 1)$ , $M (8 \mid 8 \mid 3)$ und $N (0 \mid 8 \mid 5)$ gegeben (siehe Abbildung).

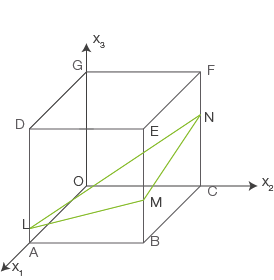
3D-Darstellung eines Würfels mit Linien und Punkten in einem Koordinatensystem.

Abb. 1

a)

(1)

Zeige, dass das Dreieck $LMN$ gleichschenklig ist.

(4P)

(2)

Zeige, dass das Dreieck $LMN$ nicht rechtwinklig ist.

(4P)

(3)

Bestimme den Flächeninhalt des Dreiecks $LMN$ .
[Zur Kontrolle: Der Flächeninhalt des Dreiecks $LMN$ beträgt $24\cdot \sqrt{2} \ [FE]$ .]

(5P)

b)

(1)

Ermittle eine Parameter- und eine Koordinatengleichung der Ebene $H$ , die die Punkte $L$ , $M$ und $N$ enthält.
[Mögliches Ergebnis für die Koordinatengleichung: $H: x_1-x_2+4x_3=12$ .]

(7P)

(2)

Bestimme die Koordinaten des Schnittpunktes der Geraden $g$ , die durch die Punkte $P (11 \mid -3 \mid 20)$ und $D$ festgelegt ist, und der Ebene $H$ .

[Zur Kontrolle: Der Schnittpunkt ist $S \left(\dfrac{58}{9} \mid \dfrac{14}{9} \mid \dfrac{16}{9}\right)$ .]

(7P)

(3)

Zeige, dass die Gerade $g$ die Ebene $H$ senkrecht schneidet.

(5P)

(4)

Bestimme das Volumen der Pyramide $LMND$ .

(5P)

c)

(1)

Bestimme den Schnittpunkt $T$ der Ebene $H$ mit der $x_3$ -Achse.
[Zur Kontrolle: $T(0 \mid 0 \mid 3)$ .]

(3P)

(2)

Skizziere in der Abbildung das Schnittgebilde, das die Ebene $H$ mit dem Würfel bildet.

(3P)

(3)

Zeige, dass das Schnittgebilde von Ebene und Würfel eine Raute ist.

(3P)

(4)

Beschreibe eine Vorgehensweise, mit der du prüfst, ob der Punkt $Q(2,5 \mid 1 \mid 2,75)$ auf derselben Seite der Ebene $H$ wie der Punkt $D$ liegt.

(4P)

Bildnachweise [nach oben]

[1]

© 2016 - SchulLV.

a)

(1)

$\blacktriangleright$ Zeigen, dass das Dreieck $\boldsymbol{\text{LMN}}$ gleichschenklig ist

Ein Dreieck heißt gleichschenklig, wenn zwei der drei Seiten gleich lang sind. Berechne die Länge der Seiten, übder die Beträge der drei Verbindungsvektoren $\overrightarrow{LM}$ , $\overrightarrow{MN}$ und $\overrightarrow{NL}$ .

$|\overrightarrow{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}$

$\begin{array}[t]{rll} &=& 2\cdot\sqrt{17} \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

\( \)

\begin{array}[t]{rll} &=& \sqrt{68} \approx 8,25 \end{array} \( \)

\( \)

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\begin{array}[t]{rll} &=& \sqrt{144} = 12 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Da die Seiten $\overrightarrow{LM}$ und $\overrightarrow{MN}$ gleich lang sind, handelt es sich um ein gleichschenkliges Dreieck.

(2)

$\blacktriangleright$ Zeigen, dass das Dreieck $\boldsymbol{\text{LMN}}$ nicht rechtwinklig ist

Um zu zeigen, dass das Dreieck $\text{LMN}$ nicht rechtwinklig ist, kannst du das Skalarprodukt verwenden. Du weißt, dass zwei Vektoren im rechten Winkel aufeinander stehen, wenn das Skalarprodukt zwischen ihnen Null ist. Wenn also das Skalarprodukt von keinen zwei der drei Vektoren Null ist, ist das Dreieck nicht rechtwinklig.

$\begin{array}[t]{rll} &=& 4\neq 0 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\begin{array}[t]{rll} &=& -72 \neq 0 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\begin{array}[t]{rll} &=& -72 \neq 0 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Da das Skalarprodukt aller Vektoren des Dreiecks ungleich 0 ist, handelt es sich nicht um ein rechtwinkliges Dreieck.

(3)

$\blacktriangleright$ Flächeninhalt des Dreiecks $\boldsymbol{\text{LMN}}$ berechnen

Um den Flächeninhalt des Dreiecks zu berechnen gibt es zwei Möglichkeiten. Die erste Möglichkeit ist die Höhe des Dreiecks zu berechnen und anschließend mit der Formel für den Flächeninhalt eines Dreiecks den Flächeninhalt zu berechnen die andere Möglichkeit ist mit Hilfe des Vektorprodukts (Kreuzprodukt) den Flächeninhalt eines Parallelogramms zu berechnen.

$\blacktriangleright$ Lösungsweg A:

Die Formel für den Flächeninhalt eines Dreiecks lautet:

$A = \frac{1}{2}\cdot g \cdot h$

Die Länge der Grundseite $\overrightarrow{NL}$ hast du bereits in der Aufgabe a) (1) berechnet. Es fehlt noch die Länge der Höhe des Dreiecks. Da es sich um ein gleichseitiges Dreieck handelt, ist die Höhe gerade die Länge des Vektors, der vom Mittelpunkt der Grundseite zum Punkt $M$ zeigt.

Die Koordinaten des Mittelpunktes kannst du mit folgender Formel berechnen:

$M\left(\frac{x_1 + x_2}{2} \left| \frac{y_1 + y_2}{2} \right| \frac{z_1 + z_2}{2} \right)$

Berechne als erstes die Koordinaten des Mittelpunktes $R$ , danach die Länge des Vektor $\overrightarrow{RM}$ und setze anschließend beide Längen in die Formel für den Flächeninhalt eines Dreiecks ein.

$R\left(\dfrac{8+ 0}{2}\; \left|\; \dfrac{0 + 8}{2} \;\right| \;\dfrac{1 + 5}{2} \right)$

$\Rightarrow R\left(4\; |\; 4\; |\; 3 \right)$

$\begin{array}[t]{rll} \left|\overrightarrow{RM}\right|&=& 4\sqrt{2} \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$A = \left |\overrightarrow{NL}\right| \cdot \left| \overrightarrow{RM}\right | = \frac{1}{2}\cdot 12 \cdot 4\sqrt{2} = 24\sqrt{2}$

Der Flächeninhalt des Dreiecks $\text{LMN}$ beträgt $24\sqrt{2}\; \text{FE}$ .

$\blacktriangleright$ Lösungsweg B:

Der Betrag des Vektorprodukts (Kreuzprodukt) enstpricht dem Flächeninhalt des durch die beiden Vektoren aufgespannten Paralellogramms. In dieser Aufgabe kannst du das Dreieck $\text{LMN}$ zu einem Parallelogramm ergänzen, den Betrag des Vektorprodukts berechnen und den berechneten Flächeninhalt durch zwei teilen.
Das Vektorprodukt ist wie folgt definiert:

$\pmatrix{a_1 \\ a_2 \\ a_3} \times \pmatrix{b_1 \\ b_2 \\ b_3} = \pmatrix{a_2b_3 - a_3b_2 \\ a_3b_1 - a_1b_3 \\ a_1b_2 - a_2b_1}$

Berechne als erstes das Vektorprodukt zwischen den beiden Vektoren $\overrightarrow{NL}$ und $\overrightarrow{LM}$ .

$\begin{array}[t]{rll} \overrightarrow{NL} \times \overrightarrow{LM} &=&\pmatrix{8 \\ -8 \\ -4} \times \pmatrix{0 \\ 8 \\ 2} \\[5pt] &=&\pmatrix{-8\cdot 2 - (-4)\cdot8\\ -4\cdot0 - 8\cdot 2 \\ 8\cdot 8-(-8)\cdot 0} \\[5pt] &=&\pmatrix{16 \\ -16 \\ 64} \end{array}$

Berechne jetzt den Betrag des Vektors und dividiere den Betrag durch zwei.

$\begin{array}[t]{rll} \left| \pmatrix{16 \\ -16 \\ 64} \right|&=& \sqrt{16^2 + (-16)^2 + 64^2} \\[5pt] &=&48\sqrt{2} \end{array}$

$48\sqrt{2} : 2 = 24\sqrt{2}$

Der Flächeninhalt des Dreiecks $\text{LMN}$ beträgt $24\sqrt{2}\; \text{FE}$ .

b)

(1)

$\blacktriangleright$ Ebenengleichung in Parameterform der Ebene H bestimmen

In dieser Aufgabe sollst du eine Ebenengleichung in Parameterform der Ebene H bestimmen, die die Punkte $\text{L}$ , $\text{M}$ und $\text{N}$ enthält. Wähle einen Ortsvektor, der zu einem der drei Punkte zeigt, als Stützvektor der Ebene und berechne anschließend die beiden Spannvektoren.

$H: \vec{x}= \overrightarrow{OL} + r\cdot \overrightarrow{LM} + s\cdot \overrightarrow{LN}$

$H: \vec{x}= \pmatrix{8 \\ 0 \\ 1} + r\cdot \pmatrix{8-8 \\ 8-0 \\ 3-1} + s\cdot \pmatrix{0-8 \\ 8-0 \\ 5-1}$

$\longrightarrow H: \vec{x}= \pmatrix{8 \\ 0 \\ 1} + r\cdot \pmatrix{0 \\ 8 \\ 2} + s\cdot \pmatrix{-8\\ 8 \\ 4}$

Eine Ebenengleichung in Parameterform lautet $H: \vec{x}= \pmatrix{8 \\ 0 \\ 1} + r\cdot \pmatrix{0 \\ 8 \\ 2} + s\cdot \pmatrix{-8\\ 8 \\ 4}$ .

$\blacktriangleright$ Ebenengleichung in Koordinatenform der Ebene $\boldsymbol{H}$ bestimmen

Um eine Ebenengleichung in Koordinatenform anzugeben, benötigst du den Normalenvektor der Ebene. Den Normalenvektor hast du vielleicht schon in der Aufgabe a) (3) berechnet, wenn nicht, kannst du den Normalenvektor mit dem Vektorprodukt (Kreuzprodukt) berechnen. Diesen kannst du dann noch mit $16$ kürzen.

$\begin{array}[t]{rll} \overrightarrow{NL} \times \overrightarrow{LM} &=&\pmatrix{8 \\ -8 \\ -4} \times \pmatrix{0 \\ 8 \\ 2} \\[5pt] &=&\pmatrix{-8\cdot 2 - (-4)\cdot8\\ -4\cdot0 - 8\cdot 2 \\ 8\cdot 8-(-8)\cdot 0} \\[5pt] &=&\pmatrix{16 \\ -16 \\ 64} \end{array}$

$\vec{n} = \pmatrix{16 \\ -16 \\ 64}$

$\vec{n_1} =\pmatrix{1 \\ -1 \\ 4}$

$\longrightarrow H: x_1 - x_2 + 4x_3 = d$

Den Parameter $d$ kannst du berechnen, indem du die Koordinaten des Stützvektors in die Ebenengleichung einsetzt.

$1\cdot 8 - 1\cdot 0 + 4\cdot 1 = 12$

$\longrightarrow H: x_1 - x_2 + 4x_3 = 12$

Die Ebenengleichung in Koordinatenform lautet $H: x_1 - x_2 + 4x_3 = 12$ .

(2)

$\blacktriangleright$ Schnittpunkt der Gerade g mit der Ebene H

In dieser Aufgabe sollst du den Schnittpunkt zwischen der Geraden g und der Ebene H berechnen. Dazu bildest du als erstes die Gerade g und anschließend kannst du den Schnittpunkt berechnen.

1. Schritt: Gerade g bilden

Die Gerade g geht durch den Punkt $P(11\;|\;-3\;|\;20)$ und den Punkt D. Wähle den Ortsvektor der zu einem der beiden Punkte zeigt als Stützvektor und berechne damit den Richtungsvektor.

$g: \overrightarrow{x}=\pmatrix{8 \\ 0 \\ 8}+ r\cdot\left(\pmatrix{11 \\ -3 \\ 20}-\pmatrix{8 \\ 0 \\ 8} \right)$

$g: \overrightarrow{x}=\pmatrix{8 \\ 0 \\ 8}+ r\cdot \pmatrix{3 \\ -3 \\ 12}$

2. Schritt: Schnittpunkt berechnen

Jetzt kannst du den allgemeinen Punkt der Geraden g in die Ebenengleichung in Koordinatenform der Ebene H einsetzen. Du erhälst eine Gleichung mit einer Unbekannten. Löse also die Gleichung nach r auf.

$G(8+3r\;|\;-3r\;|\;8+12r)$

$\begin{array}[t]{rll} 8+3r+3r+8\cdot 4+12r&=& \frac{-14}{27} \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Den Wert für $r$ kannst du in den allgemeinen Punkt der Geraden g einsetzen und du erhälst die Koordinaten des Schnittpunktes S.

$S\left(8+3\cdot\frac{-14}{27}\left|-3\cdot \frac{-14}{27} \right| 8+12\cdot \frac{-14}{27}\right)$

$S\left(\frac{58}{9}\left|\frac{14}{9} \right| \frac{16}{9}\right)$

Der Schnittpunkt der Ebene H und der Geraden g hat die Koordinaten $S\left(\frac{58}{9}\left|\frac{14}{9} \right| \frac{16}{9}\right)$ .

(3)

$\blacktriangleright$ Zeigen, dass die Gerade g dei Ebene H senkrecht schneidet

In dieser Aufgabe sollst du zeigen, dass die Gerade g die Ebene H senkrecht schneidet. Den Normalenvektor der Ebene H hast du in der Aufgabe b) (1) berechnet. Dieser steht senkrecht auf der Ebene H. Die Gerade g schneidet die Ebene H senkrecht, wenn der Normalenvektor der Ebene H und der Richtungsvektor der Geraden g vielfaches von einander sind.

Der Normalenvektor der Ebene H hat die Koordinaten $\overrightarrow{n}=\pmatrix{1 \\ -1 \\ 4}$ und der Richtungsvektor der Geraden g hat die Koordinaten $\overrightarrow{r}=\pmatrix{3 \\ -3 \\ 12}$ . Das bedeutet also:

$\overrightarrow{r}=\pmatrix{3 \\ -3 \\ 12} = 3\cdot\pmatrix{1 \\ -1 \\ 4} = 3\cdot \overrightarrow{n}$ Der Richtungsvektor der Geraden g ist vielfaches des Normalenvektors der Ebene H und die Gerade g schneidet die Ebene H senkrecht.

(4)

$\blacktriangleright$ Volumen der Pyramide $\boldsymbol{\text{LMND}}$ berechnen

In dieser Aufgabe sollst du das Volumen der Pyramide $\text{LMND}$ berechnen. Die Formel für das Volumen einer Pyramide lautet:

$V_{\text{Pyramide}} = \frac{1}{3} \cdot g \cdot h$

Den Flächeninhalt der Grundseite hast du in der Aufgabe a) (3) schon berechnet. Die Höhe der Pyramide kannst du berechnen, indem du den Abstand vom Punkt $D$ zur Ebene $H$ berechnest. Den Abstand $c$ zwischen einem Punkt und einer Ebene kannst du mit der Hesseschen Normalenform berechnen:

$\dfrac{n_1\cdot x_1+ n_2\cdot x_2+n_3\cdot x_3-d}{\left|\vec{n}\right|}=0$

Setze in die Hessesche Normalenform die Koordinaten des Punktes D ein:

$\begin{array}[t]{rll} c&=&\dfrac{1\cdot 8 - 1\cdot 0 + 4\cdot 8 -12}{\sqrt{1^2 + (-1)^2 +4^2}} \\[5pt] &=&\dfrac {28}{\sqrt{18}} = \dfrac{14\sqrt{2}}{3} \end{array}$

Jetzt kannst du den Flächeninhalt der Grundfläche und die Höhe der Pyramide in die Formel einsetzen:

$V_{\text{Pyramide}} = \dfrac{1}{3} \cdot 24\sqrt{2} \cdot \dfrac{14\sqrt{2}}{3} = 74,\overline{6}$

Das Volumen der Pyramide $\text{LMND}$ beträgt $74,\overline{6}\; VE$ .

c)

(1)

$\blacktriangleright$ Schnittpunkt T der Ebene H mit der $x_3$ -Achse berechnen

In dieser Aufgabe sollst du den Schnittpunkt T der Ebene H mit der $x_3$ -Achse berechnen. Damit die Ebene die $x_3$ - Achse schneidet, müssen die $x_1-$ und $x_2-$ Koordinaten des Schnittpunktes $T$ 0 sein.

$T(0\;|\; 0 \;|\; t)$

Wenn du den Ortsvektor des Punktes $T$ in die Ebenengleichung der Ebene $H$ einsetzt, kannst du die fehlende Koordinate des Punktes $T$ berechnen. Du erhälst zwei Gleichungen, die du nach $r$ und $s$ auflöst.

$\begin{array}[t]{rll} s &=& 1 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\begin{array}[t]{rll} r&=&-1 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Wenn du jetzt die berechneten Werte für $r$ und $s$ in die dritte Zeile der Ebenengleichung einsetzt, erhälst du die Koordinaten des Schnittpunktes $T$ .

$1 + (-1)\cdot 2 + 1\cdot (4) = 3$

Die Koordinaten des Punktes $T$ lauten $T(0\;|\; 0 \;|\; 3)$ .

(2)

$\blacktriangleright$ Schnittgebilde skizzieren

In dieser Aufgabe sollst du das Schnittgebilde, das die Ebene H mit dem Würfel bildet, skizzieren. Dazu benötigst du noch den Schnittpunkt der Ebene H mit der $x_3$ -Achse. Diesen hast du im Aufgabenteil davor berechnet. Diesen Punkt kannst du nun in das gegebene Koordinatensystem einzeichnen, und anschließend die Eckpunkte $L$ und $N$ mit dem Punkt $T$ verbinden.

Diagramm eines Quaders mit Linien und Punkten zur Veranschaulichung geometrischer Beziehungen.

Abb. 1: Skizze Schnittgebilde

(3)

$\blacktriangleright$ Zeigen, dass das Schnittgebilde eine Raute ist

In dieser Aufgabe sollst du zeigen, dass das Schnittgebilde zwischen Würfel und Ebene H eine Raute ist. Eine Raute ist ein Viereck, bei dem alle Seiten gleich lang sind. Du musst also noch zeigen, dass alle vier Seiten des Vierecks gleich lang sind. Das die Seiten $\overrightarrow{MN}$ und $\overrightarrow{LM}$ gleich lang sind hast du in der Aufgabe a) (2) schon gezeigt. Du musst also noch zeigen, dass die Seiten $\overrightarrow{LT}$ und $\overrightarrow{TN}$ genau so lang sind.

$\begin{array}[t]{rll} \left|\overrightarrow{LT}\right| &=&\ 2\sqrt{17} \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\begin{array}[t]{rll} \left|\overrightarrow{TN}\right| &=& 2\sqrt{17} \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\left|\overrightarrow{LM}\right|=2\cdot\sqrt{17}$

$\left|\overrightarrow{MN}\right|=2\cdot\sqrt{17}$

Da alle vier Seiten des Vierecks gleich lang sind, ist das Schnittgebilde zwischen dem Würfel und der Ebene H eine Raute.

(4)

$\blacktriangleright$ Vorgehensweise beschreiben

In dieser Aufgabe sollst du beschreiben, wie du vorgehen musst, um zu überprüfen, ob der Punkt $Q(2,5\;|\;1\;|\;2,75)$ auf der selben Seite der Ebene H wie der Punkt D liegt.

Wenn du dies zeigen möchtest, setzt du in die „linke Seite“ der Ebenengleichung in Koordinatenform die Koordinaten des Punktes D und berechnest somit die „rechte Seite“ der Ebenengleichung, also den Parameter c. Dieser müsste in diesem Fall größer als 12 sein. Das selbe machst du mit den Koordinaten des Punktes Q. Wenn der Parameter c dann auch größer als 12 ist, liegen die beiden Punkte auf der gleichen Seite der Ebene.

a)

(1)

$\blacktriangleright$ Zeigen, dass das Dreieck $\boldsymbol{\text{LMN}}$ gleichschenklig ist

Ein Dreieck heißt gleichschenklig, wenn zwei der drei Seiten gleich lang sind. Berechne die Länge der Seiten, übder die Beträge der drei Verbindungsvektoren $\overrightarrow{LM}$ , $\overrightarrow{MN}$ und $\overrightarrow{NL}$ .

$|\overrightarrow{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}$

$\begin{array}[t]{rll} &=& 2\cdot\sqrt{17} \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

\( \)

\begin{array}[t]{rll} &=& \sqrt{68} \approx 8,25 \end{array} \( \)

\( \)

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\begin{array}[t]{rll} &=& \sqrt{144} = 12 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Da die Seiten $\overrightarrow{LM}$ und $\overrightarrow{MN}$ gleich lang sind, handelt es sich um ein gleichschenkliges Dreieck.

(2)

$\blacktriangleright$ Zeigen, dass das Dreieck $\boldsymbol{\text{LMN}}$ nicht rechtwinklig ist

Um zu zeigen, dass das Dreieck $\text{LMN}$ nicht rechtwinklig ist, kannst du das Skalarprodukt verwenden. Du weißt, dass zwei Vektoren im rechten Winkel aufeinander stehen, wenn das Skalarprodukt zwischen ihnen Null ist. Wenn also das Skalarprodukt von keinen zwei der drei Vektoren Null ist, ist das Dreieck nicht rechtwinklig.

$\begin{array}[t]{rll} &=& 4\neq 0 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\begin{array}[t]{rll} &=& -72 \neq 0 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\begin{array}[t]{rll} &=& -72 \neq 0 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Da das Skalarprodukt aller Vektoren des Dreiecks ungleich 0 ist, handelt es sich nicht um ein rechtwinkliges Dreieck.

(3)

$\blacktriangleright$ Flächeninhalt des Dreiecks $\boldsymbol{\text{LMN}}$ berechnen

Um den Flächeninhalt des Dreiecks zu berechnen gibt es zwei Möglichkeiten. Die erste Möglichkeit ist die Höhe des Dreiecks zu berechnen und anschließend mit der Formel für den Flächeninhalt eines Dreiecks den Flächeninhalt zu berechnen die andere Möglichkeit ist mit Hilfe des Vektorprodukts (Kreuzprodukt) den Flächeninhalt eines Parallelogramms zu berechnen.

$\blacktriangleright$ Lösungsweg A:

Die Formel für den Flächeninhalt eines Dreiecks lautet:

$A = \frac{1}{2}\cdot g \cdot h$

Die Länge der Grundseite $\overrightarrow{NL}$ hast du bereits in der Aufgabe a) (1) berechnet. Es fehlt noch die Länge der Höhe des Dreiecks. Da es sich um ein gleichseitiges Dreieck handelt, ist die Höhe gerade die Länge des Vektors, der vom Mittelpunkt der Grundseite zum Punkt $M$ zeigt.

Die Koordinaten des Mittelpunktes kannst du mit folgender Formel berechnen:

$M\left(\frac{x_1 + x_2}{2} \left| \frac{y_1 + y_2}{2} \right| \frac{z_1 + z_2}{2} \right)$

Berechne als erstes die Koordinaten des Mittelpunktes $R$ , danach die Länge des Vektor $\overrightarrow{RM}$ und setze anschließend beide Längen in die Formel für den Flächeninhalt eines Dreiecks ein.

$R\left(\dfrac{8+ 0}{2}\; \left|\; \dfrac{0 + 8}{2} \;\right| \;\dfrac{1 + 5}{2} \right)$

$\Rightarrow R\left(4\; |\; 4\; |\; 3 \right)$

$\begin{array}[t]{rll} \left|\overrightarrow{RM}\right|&=& 4\sqrt{2} \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$A = \left |\overrightarrow{NL}\right| \cdot \left| \overrightarrow{RM}\right | = \frac{1}{2}\cdot 12 \cdot 4\sqrt{2} = 24\sqrt{2}$

Der Flächeninhalt des Dreiecks $\text{LMN}$ beträgt $24\sqrt{2}\; \text{FE}$ .

$\blacktriangleright$ Lösungsweg B:

Der Betrag des Vektorprodukts (Kreuzprodukt) enstpricht dem Flächeninhalt des durch die beiden Vektoren aufgespannten Paralellogramms. In dieser Aufgabe kannst du das Dreieck $\text{LMN}$ zu einem Parallelogramm ergänzen, den Betrag des Vektorprodukts berechnen und den berechneten Flächeninhalt durch zwei teilen.
Das Vektorprodukt ist wie folgt definiert:

$\pmatrix{a_1 \\ a_2 \\ a_3} \times \pmatrix{b_1 \\ b_2 \\ b_3} = \pmatrix{a_2b_3 - a_3b_2 \\ a_3b_1 - a_1b_3 \\ a_1b_2 - a_2b_1}$

Berechne als erstes das Vektorprodukt zwischen den beiden Vektoren $\overrightarrow{NL}$ und $\overrightarrow{LM}$ .

$\begin{array}[t]{rll} \overrightarrow{NL} \times \overrightarrow{LM} &=&\pmatrix{8 \\ -8 \\ -4} \times \pmatrix{0 \\ 8 \\ 2} \\[5pt] &=&\pmatrix{-8\cdot 2 - (-4)\cdot8\\ -4\cdot0 - 8\cdot 2 \\ 8\cdot 8-(-8)\cdot 0} \\[5pt] &=&\pmatrix{16 \\ -16 \\ 64} \end{array}$

Berechne jetzt den Betrag des Vektors und dividiere den Betrag durch zwei.

$\begin{array}[t]{rll} \left| \pmatrix{16 \\ -16 \\ 64} \right|&=& \sqrt{16^2 + (-16)^2 + 64^2} \\[5pt] &=&48\sqrt{2} \end{array}$

$48\sqrt{2} : 2 = 24\sqrt{2}$

Der Flächeninhalt des Dreiecks $\text{LMN}$ beträgt $24\sqrt{2}\; \text{FE}$ .

b)

(1)

$\blacktriangleright$ Ebenengleichung in Parameterform der Ebene H bestimmen

In dieser Aufgabe sollst du eine Ebenengleichung in Parameterform der Ebene H bestimmen, die die Punkte $\text{L}$ , $\text{M}$ und $\text{N}$ enthält. Wähle einen Ortsvektor, der zu einem der drei Punkte zeigt, als Stützvektor der Ebene und berechne anschließend die beiden Richtungsvektoren.

$H: \vec{x}= \overrightarrow{OL} + r\cdot \overrightarrow{LM} + s\cdot \overrightarrow{LN}$

$H: \vec{x}= \pmatrix{8 \\ 0 \\ 1} + r\cdot \pmatrix{8-8 \\ 8-0 \\ 3-1} + s\cdot \pmatrix{0-8 \\ 8-0 \\ 5-1}$

$\longrightarrow H: \vec{x}= \pmatrix{8 \\ 0 \\ 1} + r\cdot \pmatrix{0 \\ 8 \\ 2} + s\cdot \pmatrix{-8\\ 8 \\ 4}$

Eine Ebenengleichung in Parameterform lautet $H: \vec{x}= \pmatrix{8 \\ 0 \\ 1} + r\cdot \pmatrix{0 \\ 8 \\ 2} + s\cdot \pmatrix{-8\\ 8 \\ 4}$ .

$\blacktriangleright$ Ebenengleichung in Koordinatenform der Ebene H bestimmen

Um eine Ebenengleichung in Koordinatenform anzugeben, benötigst du den Normalenvektor der Ebene. Den Normalenvektor hast du vielleicht schon in der Aufgabe a) (3) berechnet, wenn nicht, kannst du den Normalenvektor mit dem Vektorprodukt (Kreuzprodukt) berechnen. Diesen kannst du dann noch mit $16$ kürzen

$\begin{array}[t]{rll} \overrightarrow{NL} \times \overrightarrow{LM} &=&\pmatrix{8 \\ -8 \\ -4} \times \pmatrix{0 \\ 8 \\ 2} \\[5pt] &=&\pmatrix{-8\cdot 2 - (-4)\cdot8\\ -4\cdot0 - 8\cdot 2 \\ 8\cdot 8-(-8)\cdot 0} \\[5pt] &=&\pmatrix{16 \\ -16 \\ 64} \end{array}$

$\vec{n} = \pmatrix{16 \\ -16 \\ 64}$

$\vec{n_1} =\pmatrix{1 \\ -1 \\ 4}$

$\longrightarrow H: x_1 - x_2 + 4x_3 = d$

Den Parameter $d$ kannst du berechnen, indem du die Koordinaten des Stützvektors in die Ebenengleichung einsetzt.

$1\cdot 8 - 1\cdot 0 + 4\cdot 1 = 12$

$\longrightarrow H: x_1 - x_2 + 4x_3 = 12$

Die Ebenengleichung in Koordinatenform lautet $H: x_1 - x_2 + 4x_3 = 12$ .

(2)

$\blacktriangleright$ Schnittpunkt der Gerade g mit der Ebene H

In dieser Aufgabe sollst du den Schnittpunkt zwischen der Geraden g und der Ebene H berechnen. Dazu bildest du als erstes die Gerade g und anschließend kannst du den Schnittpunkt berechnen.

1. Schritt: Gerade g bilden

Die Gerade g geht durch den Punkt $P(11\;|\;-3\;|\;20)$ und den Punkt D. Wähle den Ortsvektor der zu einem der beiden Punkte zeigt als Stützvektor und berechne damit den Richtungsvektor.

$g: \overrightarrow{x}=\pmatrix{8 \\ 0 \\ 8}+ r\cdot\left(\pmatrix{11 \\ -3 \\ 20}-\pmatrix{8 \\ 0 \\ 8} \right)$

$g: \overrightarrow{x}=\pmatrix{8 \\ 0 \\ 8}+ r\cdot \pmatrix{3 \\ -3 \\ 12}$

2. Schritt: Schnittpunkt berechnen

Jetzt kannst du den allgemeinen Punkt der Geraden g in die Ebenengleichung in Koordinatenform der Ebene H einsetzen. Du erhälst eine Gleichung mit einer Unbekannten. Löse also die Gleichung nach r auf.

$G(8+3r\;|\;-3r\;|\;8+12r)$

$\begin{array}[t]{rll} 8+3r+3r+8\cdot 4+4\cdot12r&=& \frac{-14}{27} \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Den Wert für $r$ kannst du in den allgemeinen Punkt der Geraden g einsetzen und du erhälst die Koordinaten des Schnittpunktes S.

$S\left(8+3\cdot\frac{-14}{27}\left|-3\cdot \frac{-14}{27} \right| 8+12\cdot \frac{-14}{27}\right)$

$S\left(\frac{58}{9}\left|\frac{14}{9} \right| \frac{16}{9}\right)$

Der Schnittpunkt zwischen der Ebene H und der Geraden g hat die Koordinaten $S\left(\frac{58}{9}\left|\frac{14}{9} \right| \frac{16}{9}\right)$ .

(3)

$\blacktriangleright$ Zeigen, dass die Gerade g dei Ebene H senkrecht schneidet

In dieser Aufgabe sollst du zeigen, dass die Gerade g die Ebene H senkrecht schneidet. Den Normalenvektor der Ebene H hast du in der Aufgabe b) (1) berechnet. Dieser steht senkrecht auf der Ebene H. Die Gerade g schneidet die Ebene H senkrecht, wenn der Normalenvektor der Ebene H und der Richtungsvektor der Geraden g vielfaches von einander sind.

Der Normalenvektor der Ebene H hat die Koordinaten $\overrightarrow{n}=\pmatrix{1 \\ -1 \\ 4}$ und der Richtungsvektor der Geraden g hat die Koordinaten $\overrightarrow{r}=\pmatrix{3 \\ -3 \\ 12}$ . Das bedeutet also:

$\overrightarrow{r}=\pmatrix{3 \\ -3 \\ 12} = 3\cdot\pmatrix{1 \\ -1 \\ 4} = 3\cdot \overrightarrow{n}$ Der Richtungsvektor der Geraden g ist vielfaches des Normalenvektors der Ebene H und die Gerade g schneidet die Ebene H senkrecht.

(4)

$\blacktriangleright$ Volumen der Pyramide $\boldsymbol{\text{LMND}}$ berechnen

In dieser Aufgabe sollst du das Volumen der Pyramide $\text{LMND}$ berechnen. Die Formel für das Volumen einer Pyramide lautet:

$V_{\text{Pyramide}} = \frac{1}{3} \cdot g \cdot h$

Den Flächeninhalt der Grundseite hast du in der Aufgabe a) (3) schon berechnet. Die Höhe der Pyramide kannst du berechnen, indem du den Abstand vom Punkt $D$ zur Ebene $H$ berechnest. Den Abstand $c$ zwischen einem Punkt und einer Ebene kannst du mit der Hesseschen Normalenform berechnen:

$\dfrac{n_1\cdot x_1+ n_2\cdot x_2+n_3\cdot x_3-d}{\left|\vec{n}\right|}=0$

Setze in die Hessesche Normalenform die Koordinaten des Punktes D ein:

$\begin{array}[t]{rll} c&=&\dfrac{1\cdot 8 - 1\cdot 0 + 4\cdot 8 -12}{\sqrt{1^2 + (-1)^2 +4^2}} \\[5pt] &=&\dfrac {28}{\sqrt{18}} = \dfrac{14\sqrt{2}}{3} \end{array}$

Jetzt kannst du den Flächeninhalt der Grundfläche und die Höhe der Pyramide in die Formel einsetzen:

$V_{\text{Pyramide}} = \dfrac{1}{3} \cdot 24\sqrt{2} \cdot \dfrac{14\sqrt{2}}{3} = 74,\overline{6}$

Das Volumen der Pyramide $\text{LMND}$ beträgt $74,\overline{6}\; VE$ .

c)

(1)

$\blacktriangleright$ Schnittpunkt T der Ebene H mit der $x_3$ -Achse berechnen

In dieser Aufgabe sollst du den Schnittpunkt T der Ebene H mit der $x_3$ -Achse berechnen. Damit die Ebene die $x_3$ - Achse schneidet, müssen die $x_1-$ und $x_2-$ Koordinaten des Schnittpunktes $T$ 0 sein.

$T(0\;|\; 0 \;|\; t)$

Wenn du den Ortsvektor des Punktes $T$ in die Ebenengleichung der Ebene $H$ einsetzt, kannst du die fehlende Koordinate des Punktes $T$ berechnen. Du erhälst zwei Gleichungen, die du nach $r$ und $s$ auflöst.

$\begin{array}[t]{rll} s &=& 1 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\begin{array}[t]{rll} r&=&-1 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Wenn du jetzt die berechneten Werte für $r$ und $s$ in die dritte Zeile der Ebenengleichung einsetzt, erhälst du die Koordinaten des Schnittpunktes $T$ .

$1 + (-1)\cdot 2 + 1\cdot (4) = 3$

Die Koordinaten des Punktes $T$ lauten $T(0\;|\; 0 \;|\; 3)$ .

(2)

$\blacktriangleright$ Schnittgebilde skizzieren

In dieser Aufgabe sollst du das Schnittgebilde, das die Ebene H mit dem Würfel bildet, skizzieren. Dazu benötigst du noch den Schnittpunkt der Ebene H mit der $x_3$ -Achse. Diesen hast du im Aufgabenteil davor berechnet. Diesen Punkt kannst du nun in das gegebene Koordinatensystem einzeichnen, und anschließend die Eckpunkte $L$ und $N$ mit dem Punkt $T$ verbinden.

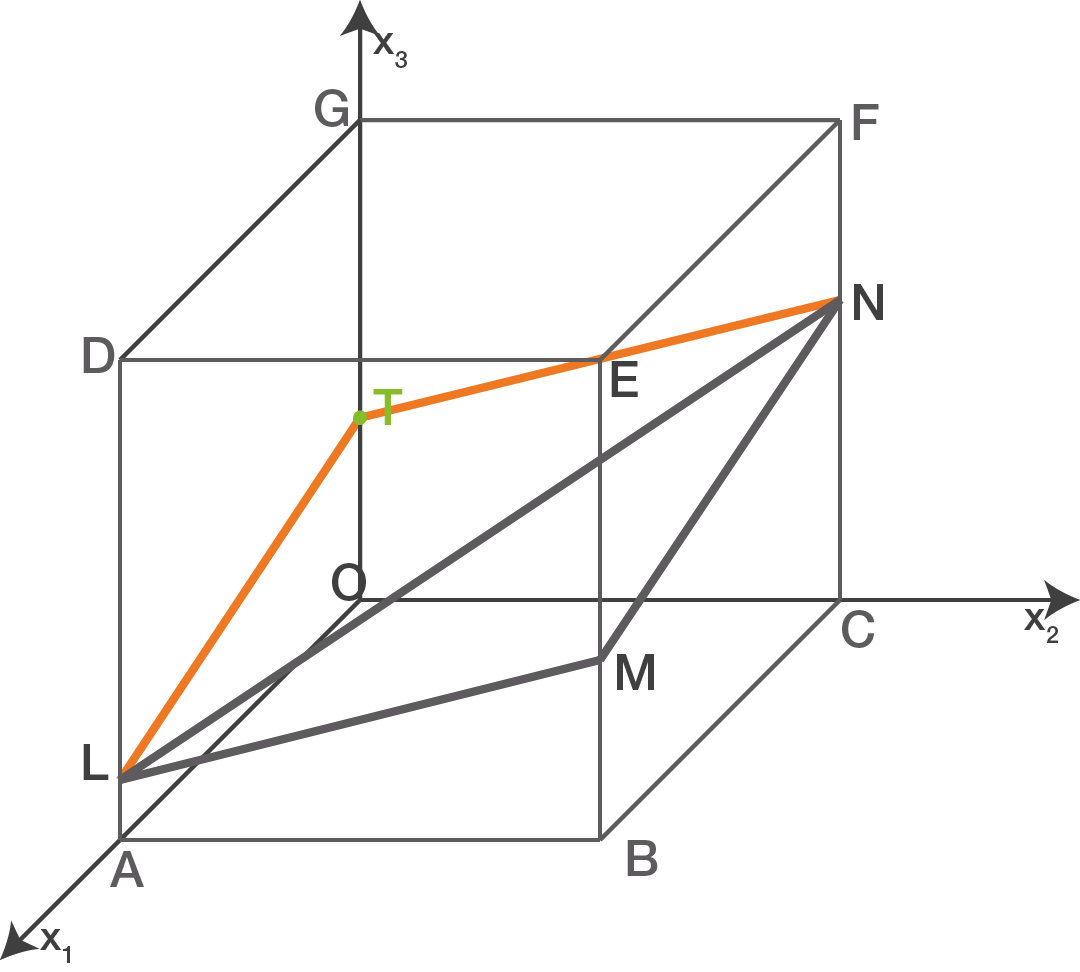Diagramm eines Quaders mit Linien und Punkten zur Veranschaulichung geometrischer Beziehungen.

Abb. 1: Skizze Schnittgebilde

(3)

$\blacktriangleright$ Zeigen, dass das Schnittgebilde eine Raute ist

In dieser Aufgabe sollst du zeigen, dass das Schnittgebilde zwischen Würfel und Ebene H eine Raute ist. Eine Raute ist ein Viereck, bei dem alle Seiten gleich lang sind. Du musst also noch zeigen, dass alle vier Seiten des Vierecks gleich lang sind. Das die Seiten $\overrightarrow{MN}$ und $\overrightarrow{LM}$ gleich lang sind hast du in der Aufgabe a) (2) schon gezeigt. Du musst also noch zeigen, dass die Seiten $\overrightarrow{LT}$ und $\overrightarrow{TN}$ genau so lang sind.

$\begin{array}[t]{rll} \left|\overrightarrow{LT}\right| &=&\ 2\sqrt{17} \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\begin{array}[t]{rll} \left|\overrightarrow{TN}\right| &=& 2\sqrt{17} \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

$\left|\overrightarrow{LM}\right|=2\cdot\sqrt{17}$

$\left|\overrightarrow{MN}\right|=2\cdot\sqrt{17}$

Da alle vier Seiten des Vierecks gleich lang sind, ist das Schnittgebilde zwischen dem Würfel und der Ebene H eine Raute.

(4)

$\blacktriangleright$ Vorgehensweise beschreiben

In dieser Aufgabe sollst du beschreiben, wie du vorgehen musst, um zu überprüfen, ob der Punkt $Q(2,5\;|\;1\;|\;2,75)$ auf der selben Seite der Ebene H wie der Punkt D liegt.

Wenn du dies zeigen möchtest, setzt du in die „linke Seite“ der Ebenengleichung in Koordinatenform die Koordinaten des Punktes D und berechnest somit die „rechte Seite“ der Ebenengleichung, also den Parameter c. Dieser müsste in diesem Fall größer als 12 sein. Das selbe machst du mit den Koordinaten des Punktes Q. Wenn der Parameter c dann auch größer als 12 ist, liegen die beiden Punkte auf der gleichen Seite der Ebene.