Teil A: Ohne Hilfsmittel

Gegeben sind die Funktionen $g$ und $h$ durch die Gleichungen

$g(x) = x^2 -x+1\,$ mit $x\in \mathbb{R}$ und

$h(x) = -x^2-5x +1\,$ mit $x\in \mathbb{R}.$

(1)

Zeige, dass sich die Graphen von $g$ und $h$ nur für $x=-2$ und $x=0$ schneiden.

(2)

Berechne den Inhalt der Fläche, die die Graphen von $g$ und $h$ einschließen.

(2 + 4 Punkte)

Gegeben ist die Funktion $f$ durch die Gleichung $f(x)= x\cdot \mathrm e^{2x+2},$ $x\in \mathbb{R}.$

(1)

Bestimme die erste Ableitung.

Für die zweite Ableitung von $f$ gilt: $\(f$

(2)

Bestimme die Koordinaten des Wendepunktes.
Hinweis: Auf den Nachweis einer hinreichenden Bedingung kann verzichtet werden.

(3 + 3 Punkte)

In einer Urne befinden sich drei rote und sieben weiße Kugeln.

(1)

Zweimal nacheinander wird jeweils eine Kugel zufällig entnommen und wieder zurückgelegt.

Berechne die Wahrscheinlichkeit dafür, dass höchstens eine der entnommenen Kugeln weiß ist.

(2)

Zehnmal nacheinander wird jeweils eine Kugel zufällig entnommen und wieder zurückgelegt. Die Zufallsgröße $X$ beschreibt die Anzahl der entnommenen weißen Kugeln.

Begründe ohne Berechnung von Wahrscheinlichkeiten, dass keine der folgenden Abbildungen 1 und 2 die Wahrscheinlichkeitsverteilung von $X$ darstellt.

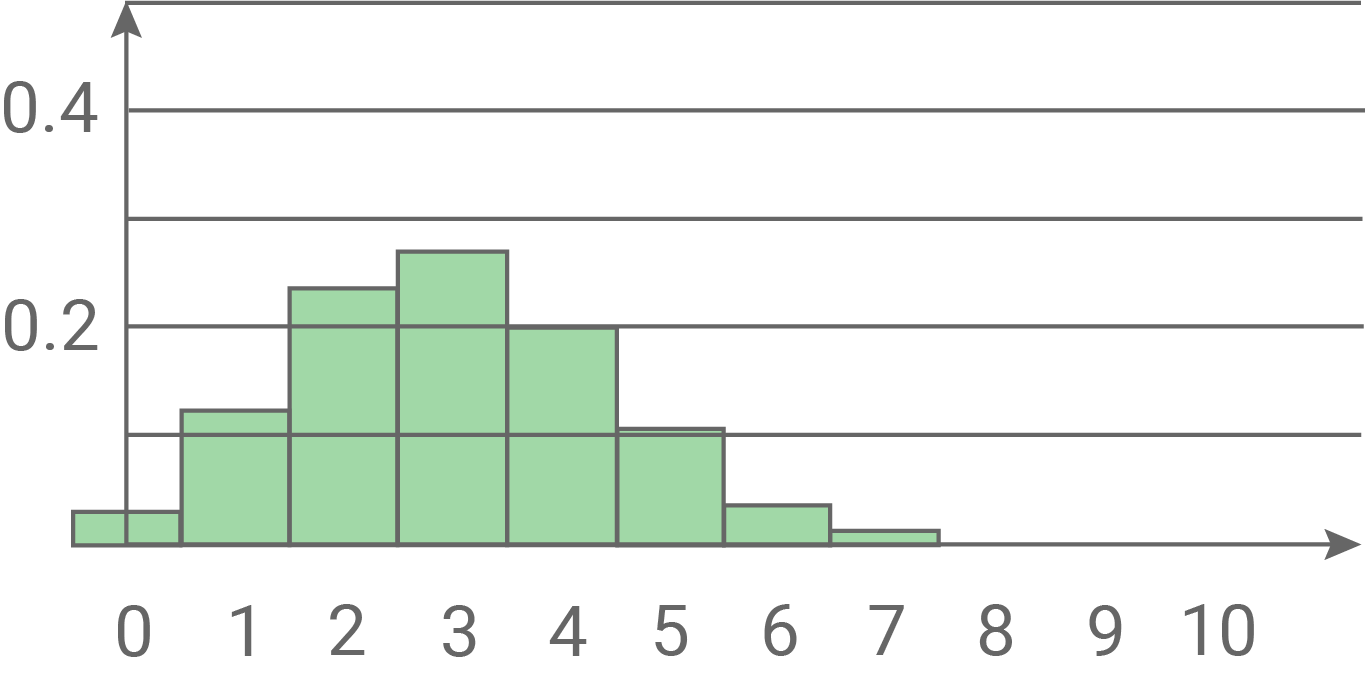
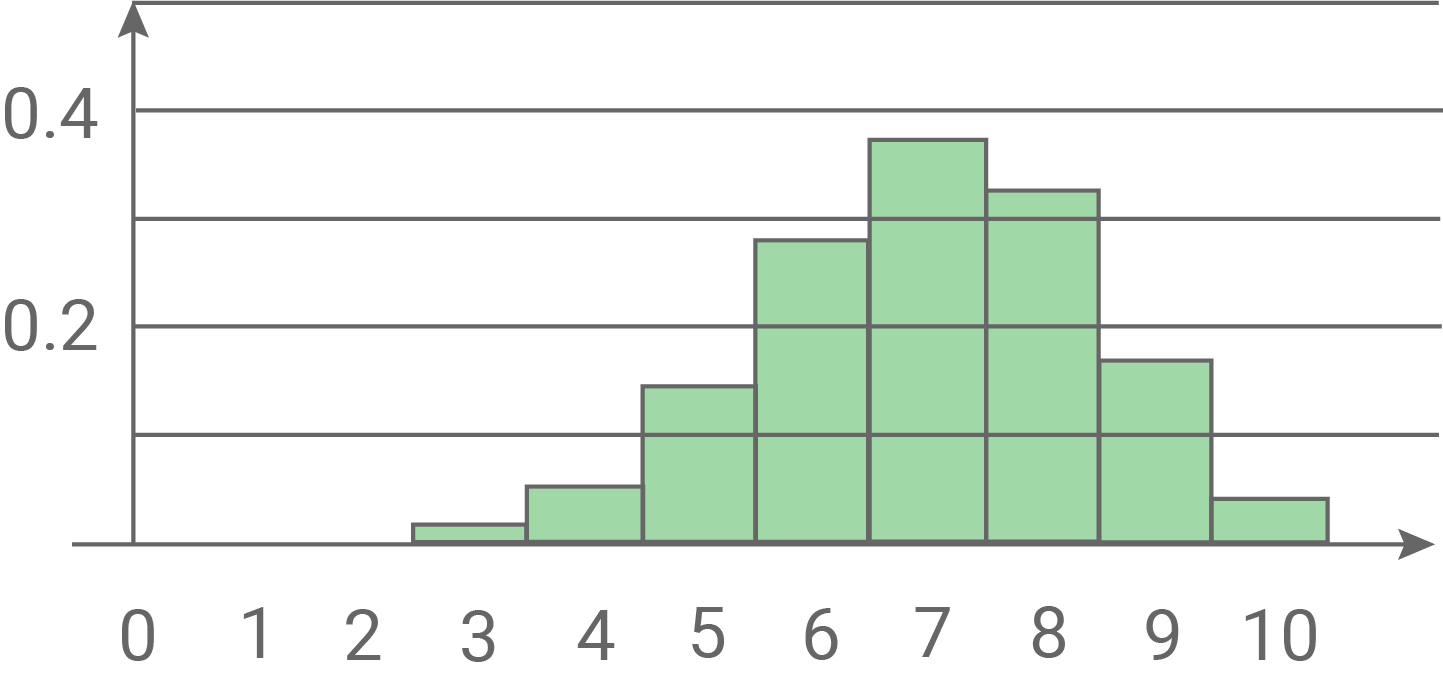
Abbildung 1

Abbildung 2

(3 + 3 Punkte)

In einem kartesischen Koordinatensystem sind die Punkte $A(0\mid 2\mid 2),$ $B(4\mid -1\mid z)$ und $C(-3\mid y\mid 6)$ mit $y,z\in \mathbb{R}$ gegeben.

(1)

$B$ liegt auf der Geraden

$g:\, \overrightarrow{x} = \pmatrix{0\\2\\2} + r\cdot \pmatrix{-1\\0,75\\-2}$ mit $r\in \mathbb{R}.$

Bestimme den Wert von $z.$

(2)

Zeige, dass der Abstand von $A$ und $C$ mindestens $5$ beträgt.

(3 + 3 Punkte)

(1)

$\blacktriangleright$ Schnittstellen zeigen

$\begin{array}[t]{rll} g(x) &=& h(x) \\[5pt] ... \\[5pt] 2x_2 &=& -4 &\quad \scriptsize \mid\;:2 \\[5pt] x_2 &=& -2 \end{array}$

Vollständige Lösung anzeigen

Die Gleichung $g(x) =h(x)$ hat genau zwei Lösungen, $x_1 = 0$ und $x_2 = -2.$ Die Graphen von $g$ und $h$ schneiden sich also nur an diesen beiden Stellen.

(2)

$\blacktriangleright$ Flächeninhalt berechnen

$\displaystyle\int_{-2}^{0}\left(g(x)-h(x) \right)\;\mathrm dx =- \frac{8}{3}$

Vollständige Lösung anzeigen

Der Flächeninhalt der vom Graphen von $g$ und $h$ eingeschlossenen Fläche beträgt $\frac{8}{3}\,\text{FE}.$

(1)

$\blacktriangleright$ Ableitung bestimmen

Verwende die Produktregel:

$f‘(x)=\left(1+2x \right)\cdot \mathrm e^{2x+2}$

Vollständige Lösung anzeigen

(2)

$\blacktriangleright$ Koordinaten des Wendepunktes bestimmen

1. Schritt: Notwendiges Kriterium für Wendestellen anwenden

$x=-1$

Vollständige Lösung anzeigen

$x=-1$ ist die einzige mögliche Wendestelle von $f.$ Eine Überprüfung einer hinreichenden Bedingung ist laut Aufgabenstellung nicht erforderlich.

2. Schritt: $y$ -Koordinate bestimmen

$f(-1)=-1$

Vollständige Lösung anzeigen

Der Wendepunkt des Graphen von $f$ hat die Koordinaten $W(-1\mid -1).$

(1)

$\blacktriangleright$ Wahrscheinlichkeit berechnen

$... = 51\,\%$

Vollständige Lösung anzeigen

(2)

$\blacktriangleright$ Passende Abbildung begründen

$X$ ist binomialverteilt mit $n=10$ und $p=0,7.$ Für den Erwartungswert gilt also:

$\mu(X) = 10\cdot 0,7 = 7$

Bei einer binomialverteilten Zufallsgröße ist der Erwartungswert der Wert mit der höchsten Wahrscheinlichkeit.
In Abbildung 1 ist aber $3$ der Wert mit der höchsten Wahrscheinlichkeit. Diese Abbildung kann also nicht die Wahrscheinlichkeitsverteilung einer binomialverteilten Zufallsgröße mit dem Erwartungswert $7$ darstellen.

Abbildung 2 kann die Wahrscheinlichkeitsverteilung von $X$ nicht darstellen, da die Summe aller dargestellten Wahrscheinlichkeiten hier größer als $1$ ist. Die Summe aller Wahrscheinlichkeiten einer Wahrscheinlichkeitsverteilung beträgt aber immer $1.$