Wahlpflichtteil

Aufgabe 1 - Analysis

Der Graph einer quadratischen Funktion $f$ verläuft durch den Koordinatenursprung.

Die Tangente an diesen Graphen im Punkt $(2\mid f(2))$ hat die Gleichung $y=4\cdot x-2.$

Bestimme eine Funktionsgleichung von $f.$

(5 Punkte)

Aufgabe 2 - Analysis

Betrachtet werden die Exponentialfunktionen $f$ und $g.$

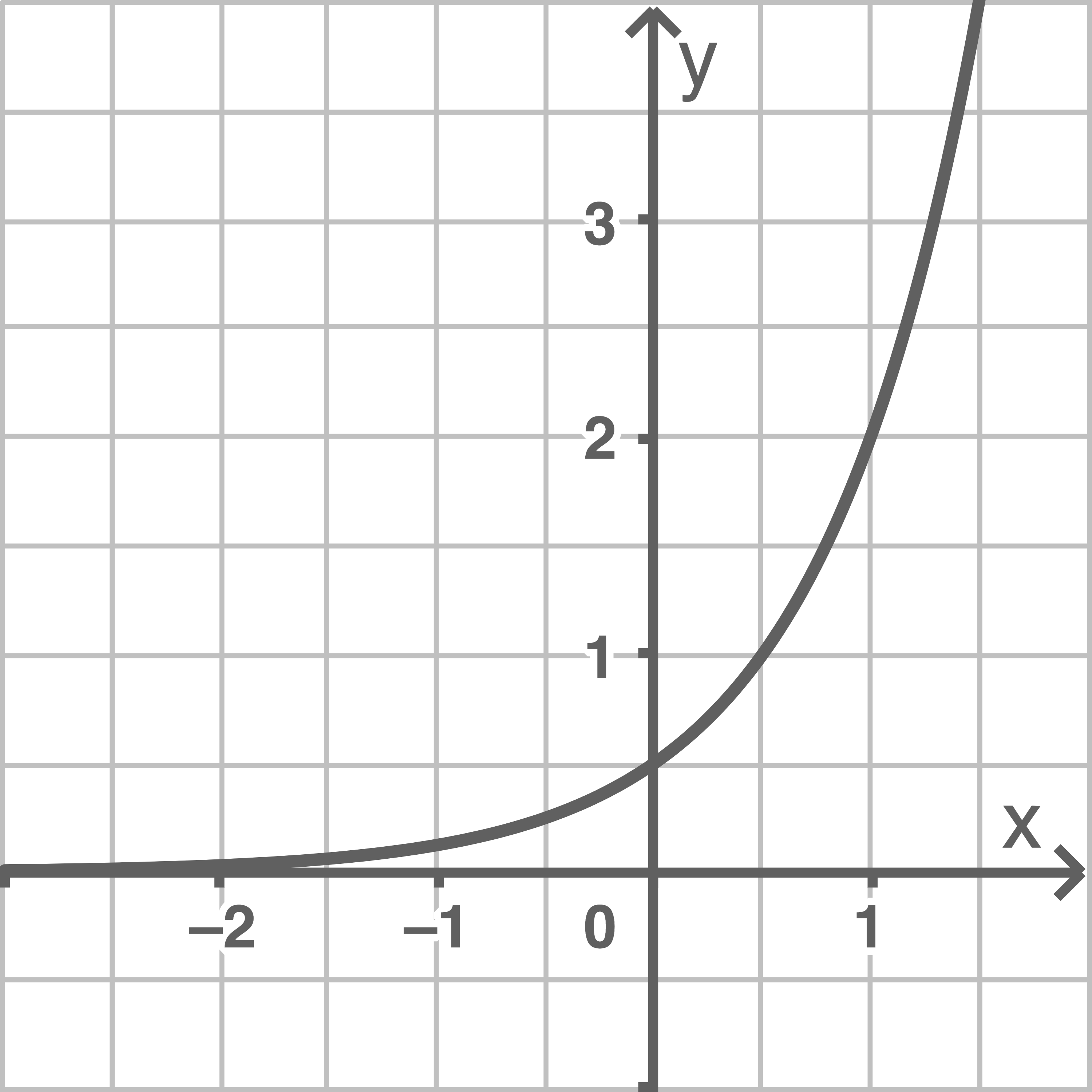
Die Abbildung zeigt den Graphen von $f$ mit $f(x)=a \cdot b^{x}$ und $a, b \in \mathbb{R}$ sowie $a>0$ und $b>0$ . Bestimme die passenden Werte von $a$ und $b$ .

Der Graph der in $\mathbb{R}$ definierten Funktion $g$ mit $g(x)=3^{x}$ wird um 2 in negative $x$ -Richtung verschoben.

Zeige, dass der dadurch entstehende Graph auch durch eine Streckung des Graphen von $g$ in $y$ -Richtung erzeugt werden kann.

(2 + 3 Punkte)

Aufgabe 3 - Vektorielle Geometrie

Gegeben ist der Punkt $P(4\mid6\mid4)$ und die Ebene $E:\,\vec{x}=\pmatrix{1\\2\\3}+t\cdot\pmatrix{0\\2\\1}+s\cdot\pmatrix{3\\0\\-1}$ ; $t,\,s\,\in\mathbb{R}$ .

Weise nach, dass der Punkt $P$ in der Ebene $E$ liegt.

Die Gerade $g$

liegt in der Ebene $E$ ,
geht durch den Punkt $P$ und
hat keinen Schnittpunkt mit der $xy$ -Ebene.

Gib eine Gleichung der Geraden $g$ an.

(2 + 3 Punkte)

Aufgabe 4 - Vektorielle Geometrie

Gegeben sind die Punkte $A(-2\mid 1\mid -2),$ $B(1\mid 2\mid -1)$ und $C(1\mid 1\mid 4)$ sowie für eine reelle Zahl $d$ der Punkt $D(d\mid 1\mid 4).$

Zeige, dass $A,$ $B$ und $C$ Eckpunkte eines Dreiecks sind.

Gib eine Gleichung der Ebene an, in der dieses Dreieck liegt.

Das Dreieck $ABD$ ist im Punkt $B$ rechtwinklig.

Ermittle den Wert von $d.$

(3 + 2 Punkte)

Aufgabe 5 - Stochastik

In einem Behälter befinden sich 2 blaue und 3 weiße Kugeln.

Zwei Kugeln werden nacheinander zufällig ohne Zurücklegen gezogen.

Gib für die folgenden Ereignisse jeweils einen Term zur Berechnung der Wahrscheinlichkeit an.

Das Berechnen der Ergebnisse ist nicht nötig.

$A:$

"Beide Kugeln sind blau."

$B:$

"Mindestens eine Kugel ist weiß."

$C:$

"Eine Kugel ist weiß und eine blau."

Bestimme, wie viele grüne Kugeln zusätzlich in den Behälter gelegt werden müssen, damit die Wahrscheinlichkeit, beim einmaligen Ziehen zufällig eine grüne Kugel zu ziehen, $\dfrac{2}{3}$ beträgt.

(3 + 2 Punkte)

Aufgabe 6 - Stochastik

Überprüfungen in einer Kleinstadt haben gezeigt, dass ein Viertel der Radfahrenden keinen Helm trägt.

Gib einen Term an, mit dem die Wahrscheinlichkeit dafür berechnet werden kann, dass unter 75 zufällig ausgewählten Radfahrenden genau 20 keinen Helm tragen.

Untersuche, wie viele Radfahrende man mindestens überprüfen muss, damit die Wahrscheinlichkeit, nur Radfahrende mit Helm anzutreffen, kleiner als $\displaystyle \frac{1}{2}$ ist.

(2 + 3 Punkte)

(10 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1 - Analysis

Die Gleichung einer quadratischen Funktion hat die Form $f(x)=ax^2 +bx+c.$

Da $f$ durch den Koordinatenursprung verläuft, muss gelten:

$\begin{array}[t]{rll} f(0)&=& 0 & \\[5pt] a \cdot 0^2 +b \cdot 0+c&=& 0& \\[5pt] c&=& 0& \\[5pt] \end{array}$

Aus der Tangentengleichung am Punkt $(2\mid f(2))$ ergeben sich folgende Bedingungen:

$\text{I}\; : \; \; f(2)=4\cdot 2 -2=6$

$\(\text{II}: \;f$

Erste Ableitung von $f$ bilden:

$\(f$

Einsetzen von $\text{II}$ in die Ableitungsfunktion liefert:

$\(\begin{array}[t]{rll} f$

Durch Einsetzen von $b$ in $\text{I}$ folgt nun:

$\begin{array}[t]{rll} f(2)&=& 6 & \\[5pt] a\cdot 2^2 +b\cdot 2&=& 6& \quad \scriptsize \mid\; b= 4-4a \\[5pt] 4a +2\cdot (4-4a) &=& 6 \\[5pt] 4a +8 -8a &=& 6 &\quad \scriptsize \mid\; -8\\[5pt] -4a &=& -2 &\quad \scriptsize \mid\; :(-4)\\[5pt] a &=& \dfrac{1}{2} \end{array}$

Für $b$ ergibt sich damit:

$b = 4-4\cdot \dfrac{1}{2} = 2$

Eine Funktionsgleichung von $f$ lautet also:

$f(x)=\dfrac{1}{2}x^2 +2x$

Lösung 2 - Analysis

Aus dem Graphen können eindeutig die Punkte $P_1(0\mid 0,5)$ und $P_2(1\mid 2)$ der Exponentialfunktion entnommen werden.

$P_1$ in $f$ einsetzen:

$\begin{array}[t]{rll} f(0)&=& 0,5 & \\[5pt] a\cdot b^0&=& 0,5 & \\[5pt] a&=& 0,5 & \\[5pt] \end{array}$

$P_2$ und $a$ in $f$ einsetzen:

$\begin{array}[t]{rll} f(1)&=& 2& \\[5pt] 0,5\cdot b^1&=& 2& \quad \scriptsize \mid :0,5\\[5pt] b &=& 4 \end{array}$

Die Abbildung zeigt folglich den Graphen von $f(x)=0,5\cdot 4^x.$

Verschiebung von $g$ um $2$ in negative $x$ -Richtung:

$g_2(x)=3^{x+2}$

Anwendung der Potenzgesetze:

$3^{x+2}=3^x\cdot 3^2=3^x\cdot 9$

Der Multiplikationsfaktor $9$ streckt den Graphen von $g$ in $y$ -Richtung.

Lösung 3 - Vektorielle Geometrie

Einsetzen des Ortsvektors von $P$ in die Geradengleichung liefert:

Vollständigen Rechenweg anzeigen

$\pmatrix{3\\4\\1} = ...$

Aus der ersten Zeile folgt:

$\begin{array}[t]{rll} 3&=& 3s&\quad \scriptsize \mid\;:3 \\[5pt] 1&=& s \end{array}$

Aus der zweiten Zeile ergibt sich:

$\begin{array}[t]{rll} 4&=& 2t&\quad \scriptsize \mid\; :2\\[5pt] 2&=& t \end{array}$

Durch Einsetzen der Werte in die dritte Zeile folgt:

$\begin{array}[t]{rll} 1&=& t-s & \\[5pt] 1&=& 2-1& \\[5pt] 1&=& 1 \end{array}$

Der Punkt $P$ liegt somit in der Ebene $E.$

Die Gerade $g$ schneidet die $xy$ -Ebene nicht, wenn alle Punkte, die auf ihr liegen, die gleichen $z$ -Koordinaten haben.

Es wird also ein weiterer Punkt $Q$ benötigt, der in $E$ liegt und die gleiche $z$ -Koordinate wie $P$ besitzt:

$Q(q_1\mid q_2\mid 4)$

Für die Koordinaten des Punktes $Q$ muss also gelten:

$\begin{array}[t]{rll} q_1&=& 1+ 3s\\ q_2&=& 2 +2t\\ 4&=& 3 + t-s\\ \end{array}$

Eine mögliche Lösung für die Koordinaten von $Q$ ist für $s=0$ und $t=1$ beispielsweise $Q(1\mid4\mid4).$

Mit den Punkten $Q$ und $P$ folgt nun eine Geradengleichung von $g$ mit:

$g_{PQ}:\,\vec{x}=\pmatrix{4\\6\\4}+r\cdot\pmatrix{-3\\-2\\0}$ mit $r\in\mathbb{R}$

Lösung 4 - Vektorielle Geometrie

Zeigen, dass die Punkte ein Dreieck bilden

Die drei Punkte $A,$ $B$ und $C$ sind nur dann nicht die Eckpunkte eines Dreiecks, wenn sie auf einer Geraden liegen. Das ist genau dann der Fall, wenn die beiden Vektoren $\overrightarrow{AB}$ und $\overrightarrow{AC}$ linear abhängig sind.

Es muss also ein $a\in \mathbb{R}$ geben, sodass gilt:

$\begin{array}[t]{rll} \overrightarrow{AB}&=& a\cdot \overrightarrow{AC} & \\[5pt] \pmatrix{3\\1\\1}&=& a\cdot \pmatrix{3\\0\\6} & \\[5pt] \end{array}$

Da $1\neq0$ ist, sind die beiden Vektoren also nicht linear abhängig.

Somit sind die Punkte $A$ , $B$ und $C$ Eckpunkte eines Dreiecks.

Ebenengleichung angeben

$E: \quad \overrightarrow{x}= \overrightarrow{OA}+s \cdot\overrightarrow{AB}+t\cdot\overrightarrow{AC}$

Vollständige Ebenengleichung anzeigen

Das Dreieck $ABD$ ist genau dann rechtwinklig im Punkt $B,$ wenn die beiden an $B$ angrenzenden Dreiecksseiten und damit auch die zugehörigen Verbindungsvektoren $\overrightarrow{AB}$ und $\overrightarrow{BD}$ orthogonal zueinander verlaufen.

Es muss also gelten:

$\begin{array}[t]{rll} \overrightarrow{AB}\circ \overrightarrow{BD}&=& 0 \\[5pt] \pmatrix{3\\1\\1}\circ \pmatrix{d-1\\-1\\ 5}&=& 0 \\[5pt] \end{array}$

Auflösen nach $d$ ergibt nun:

Rechenweg anzeigen

$d= -\dfrac{1}{3}$

Für $d=-\dfrac{1}{3}$ ist das Dreieck $ABD$ somit rechtwinklig im Punkt $B.$

Lösung 5 - Stochastik

Mit den Pfadregeln folgt:

$\begin{array}[t]{rll} P(A)&=& P(b,b) &\\[5pt] &=& \dfrac{2}{5}\cdot \dfrac{1}{4} \end{array}$

$\begin{array}[t]{rll} P(B)&=& P(w,w)+ P(w,b)+P(b,w) &\\[5pt] &=&\dfrac{3}{5}\cdot \dfrac{2}{4} + \dfrac{3}{5}\cdot \dfrac{2}{4} +\dfrac{2}{5}\cdot \dfrac{3}{4} \end{array}$

$\begin{array}[t]{rll} P(C) &=& P(w,b)+P(b,w) &\\[5pt] &=& \dfrac{3}{5}\cdot \dfrac{2}{4} + \dfrac{2}{5}\cdot \dfrac{3}{4} \end{array}$

Werden $x$ grüne Kugeln hinzugefügt, dann befinden sich $5+x$ Kugeln im Behälter.

Die Wahrscheinlichkeit, eine grüne Kugel zu ziehen, beträgt dann $\dfrac{x}{5+x}.$

Gleichsetzen mit $\dfrac{2}{3}$ liefert:

$\begin{array}[t]{rll} \dfrac{x}{5+x} &=& \dfrac{2}{3} &\quad \scriptsize \mid\; \cdot (5+x) \\[5pt] x &=&\dfrac{10}{3} + \dfrac{2}{3}x &\quad \scriptsize \mid\;-\dfrac{2}{3}x \\[5pt] \dfrac{1}{3}x&=& \dfrac{10}{3} &\quad \scriptsize \mid\;\cdot 3 \\[5pt] x &=& 10 \end{array}$

Es müssen also $10$ grüne Kugeln hinzugefügt werden.

Lösung 6 - Stochastik

$X$ beschreibt die Anzahl der Radfahrenden ohne Helm und ist binomialverteilt mit $B_{75; 0,25}$ .

Der gesuchte Term folgt mit:

$P(X=20)=\pmatrix{75\\20}\cdot 0,25^{20}\cdot 0,75^{55}$

$X$ beschreibt die Anzahl der Radfahrenden ohne Helm und ist binomialverteilt mit $B_{n; 0,25}$ .

$\begin{array}[t]{rll} P(X=0)&\lt& \dfrac{1}{2} &\quad \\[5pt] \pmatrix{n\\0}\cdot 0,25^{0}\cdot 0,75^{n}&\lt& \dfrac{1}{2} &\quad \\[5pt] 1 \cdot 0,75^n&\lt& \dfrac{1}{2} &\quad \\[5pt] \left(\dfrac{3}{4}\right)^n&\lt&\dfrac{1}{2}&\quad \\[5pt] \end{array}$

Systematisches Probieren liefert:

Für $n=1$ gilt: $\left(\dfrac{3}{4}\right)^1=\dfrac{3}{4} \gt \dfrac{1}{2}$

Für $n=2$ gilt: $\left(\dfrac{3}{4}\right)^2=\dfrac{9}{16} \gt \dfrac{1}{2}$

Für $n=3$ gilt: $\left(\dfrac{3}{4}\right)^3=\dfrac{27}{64} \lt \dfrac{1}{2}$

Daraus folgt, dass mindestens drei Radfahrende überprüft werden müssen, damit die Wahrscheinlichkeit, nur Radfahrende mit Helm anzutreffen, kleiner als $\displaystyle \frac{1}{2}$ ist.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?