Aufgabe 4

Im Jahr 2018 wurden in Nordrhein-Westfalen etwa $390\,000$ praktische Führerscheinprüfungen abgelegt. Der relative Anteil von bestandenen Prüfungen lag in dem Jahr bei etwa $70 \,\%.$

Bei einer Fahrschulkette geht man am Standort Düsseldorf für das Jahr 2021 von insgesamt $250$ praktischen Führerscheinprüfungen aus. Die Zufallsvariable $X$ beschreibt die Anzahl unter diesen $250$ praktischen Prüfungen, die bestanden werden. Es wird modellhaft angenommen, dass $X$ binomialverteilt mit $p = 0,7$ ist.

(1)

Ermittle für die folgenden Ereignisse jeweils die Wahrscheinlichkeit:

E1: "Es werden höchstens $160$ praktische Prüfungen bestanden."

E2: "Es werden mindestens $80\; \%$ der praktischen Prüfungen bestanden."

E3: "Die Anzahl der bestandenen praktischen Prüfungen weicht um mindestens eine Standardabweichung vom Erwartungswert ab."

(2)

Im Folgenden ist $k$ eine ganze Zahl mit $0\leq k\leq250.$

(i)

Bestimme für $k = 165$ die Wahrscheinlichkeit $P(X \geq k)$ , dass mindestens $k$ praktische Prüfungen bestanden werden.

(ii)

Beschreibe, wie sich die in (i) bestimmte Wahrscheinlichkeit ändert, wenn der Wert von $k$ verändert wird.

(iii)

Die Wahrscheinlichkeit, für mindestens $k$ bestandene praktische Prüfungen soll kleiner oder gleich $60\; \%$ sein.

Ermittle, wie groß $k$ in diesem Fall mindestens gewählt werden muss.

(8 + 6 Punkte)

Die Fahrschulkette plant für das Jahr 2022 die Eröffnung einer Filiale in Soest. Die Zentrale stellt als Anspruch an die Ausbildungsqualität, dass von den praktischen Prüfungen im Schnitt mindestens $70 \;\%$ bestanden werden. Man prognostiziert für Soest, dass $200$ praktische Prüfungen im Jahr 2022 abgelegt werden. Wenn davon mindestens $140$ Prüfungen bestanden werden, will die Zentrale davon ausgehen, dass auch in Soest aufgrund der Ausbildungsqualität jede Prüfung mit einer Wahrscheinlichkeit von mindestens $70 \;\%$ bestanden wird. Es wird modellhaft angenommen, dass die Anzahl $Y$ der bestandenen Prüfungen unter den $200$ prognostizierten Prüfungen binomialverteilt ist.

(1)

Bestimme die Wahrscheinlichkeit, dass die Zentrale zu der Einschätzung kommt, dass in Soest jede Prüfung mit einer Wahrscheinlichkeit von mindestens $70 \;\%$ bestanden wird, obwohl die Prüfungen tatsächlich nur mit einer Wahrscheinlichkeit von jeweils $65\;\%$ bestanden werden.

(2)

Die Abbildung zeigt das Histogramm zu $P_{200;0,7}(Y=k)$ , also für den Fall, dass $p=0,7$ gilt.

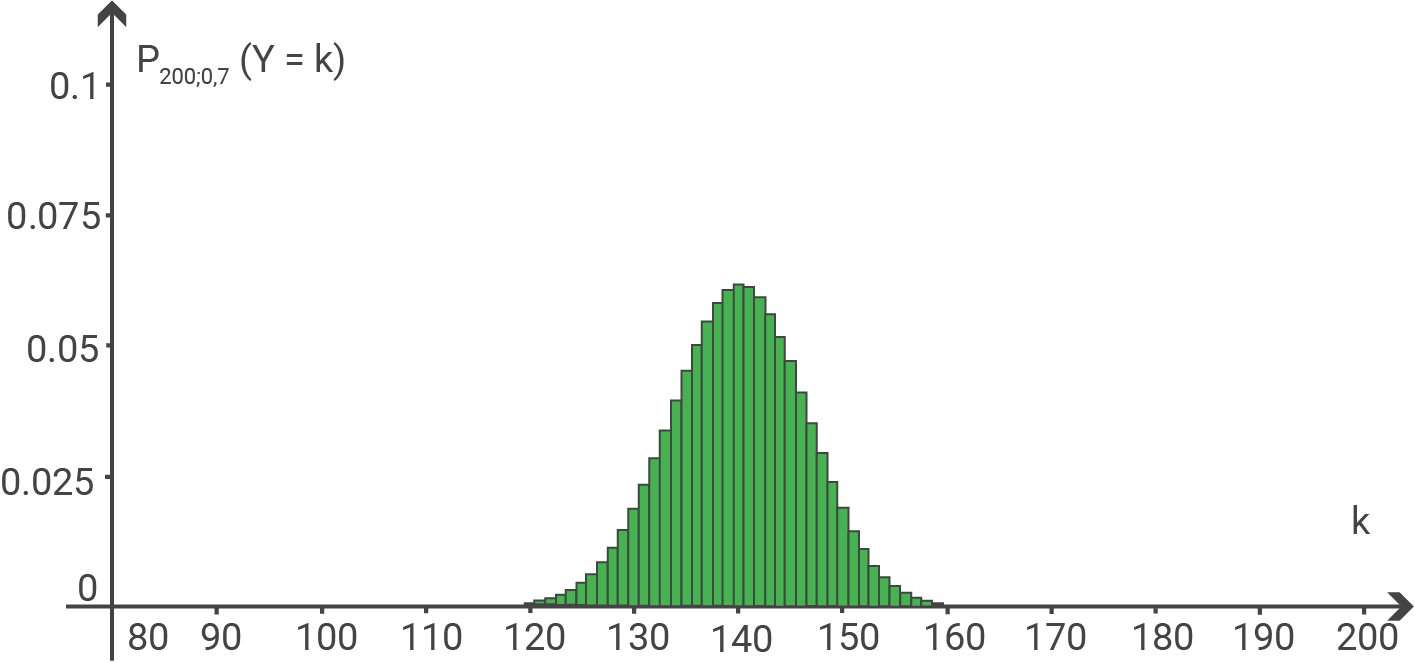Histogramm mit Wahrscheinlichkeitsverteilung, zeigt Werte von k auf der x-Achse und Wahrscheinlichkeiten auf der y-Achse.

Falls von den $200$ prognostizierten praktischen Prüfungen in Soest z.B. nur $130$ bestanden werden, kommt die Zentrale zu der Einschätzung, dass in Soest jede Prüfung mit einer Wahrscheinlichkeit von weniger als $70\; \%$ bestanden wird.

Erkläre mithilfe des Histogramms, warum die Zentrale bei dieser Einschätzung einen Irrtum begangen haben könnte.

(3 + 3 Punkte)