Aufgabe 4
Die Entwicklung der Population einer bestimmten Seevogelart in einem festgelegten Beobachtungsgebiet wird durch folgende Modellannahmen beschrieben:
Die Überlebensrate der Vögel in den ersten beiden Lebensjahren wird jeweils mit 0,6 angenommen, in den späteren Lebensjahren mit 0,8. Die erste Brut findet im 3. Lebensjahr statt, der Bruterfolg wird mit 0,5 Jungvögeln pro Elternvogel und Jahr angenommen.
Die Vögel werden in drei Altersgruppen eingeteilt, deren Anzahlen
 Anzahl der Jungvögel im 1. Lebensjahr (Altersgruppe 1)
Anzahl der Jungvögel im 1. Lebensjahr (Altersgruppe 1)
 Anzahl der Vögel im 2. Lebensjahr (Altersgruppe 2)
Anzahl der Vögel im 2. Lebensjahr (Altersgruppe 2)
 Anzahl der Altvögel, die älter als 2 Jahre sind (Altersgruppe 3)
durch jährliche Zählungen ermittelt und jeweils zu einer Verteilung1
Anzahl der Altvögel, die älter als 2 Jahre sind (Altersgruppe 3)
durch jährliche Zählungen ermittelt und jeweils zu einer Verteilung1  zusammengefasst werden. Die Matrix
zusammengefasst werden. Die Matrix  beschreibt dieses Modell.
beschreibt dieses Modell.
1 Verteilungsvektoren werden der Einfachheit halber im Folgenden kurz „Verteilung“ genannt.
a) Die aktuelle Zählung ergibt  ,
,  ,
,  .
.
- Berechnen Sie, ausgehend von diesen Zahlen, die Verteilung der Vögel nach einem Jahr und nach zwei Jahren.
- Bestimmen Sie die Verteilung der Vögel, die sich aus dem Modell für das Vorjahr ergäbe.
- Fünf Elemente der Matrix L haben den Wert Null.
Erklären Sie für jedes dieser Elemente aus dem Sachzusammenhang heraus, warum es den Wert Null hat.
(5P + 5P + 5P)
b)
 Jungvögeln pro Elternvogel und Jahr erhöht.
Jungvögeln pro Elternvogel und Jahr erhöht.
- Untersuchen Sie, ob es eine von
verschiedene stationäre Verteilung gibt, d.h. eine Verteilung, die sich innerhalb eines Jahres nicht ändert.
- Wenn sich die Population sehr lange nach dem durch die Matrix L beschriebenen Modell entwickelt, wird sie sich pro Jahr näherungsweise um einen festen Prozentsatz p verkleinern. Nach 20 Jahren wird sie noch aus insgesamt 17.870 Vögeln, nach weiteren 10 Jahren aus 15.422 Vögeln bestehen.
Berechnen Sie anhand dieser Angaben einen Näherungswert für den Prozentsatz p. - Langfristig gilt:
.
Ermitteln Sie näherungsweise, in wie viel Jahren sich unter dieser Voraussetzung die Population jeweils halbiert.
- Zeigen Sie, dass die Verteilung
für jede positive ganze Zahl
eine stationäre Verteilung ist.
- Berechnen Sie für eine konkrete stationäre Verteilung aus
die prozentualen Anteile jeder der 3 Altergruppen an der Gesamtzahl der Vögel und zeigen Sie, dass sich für jede stationäre Verteilung aus
unabhängig von
dieselben Anteile ergeben.
(6P + 5P + 5P + 4P + 6P)
c) Die Entwicklung einer Population einer anderen Vogelart ist durch den folgenden Übergangsgraphen gegeben, wobei sich die Übergangsquoten wieder auf ein Jahr beziehen.
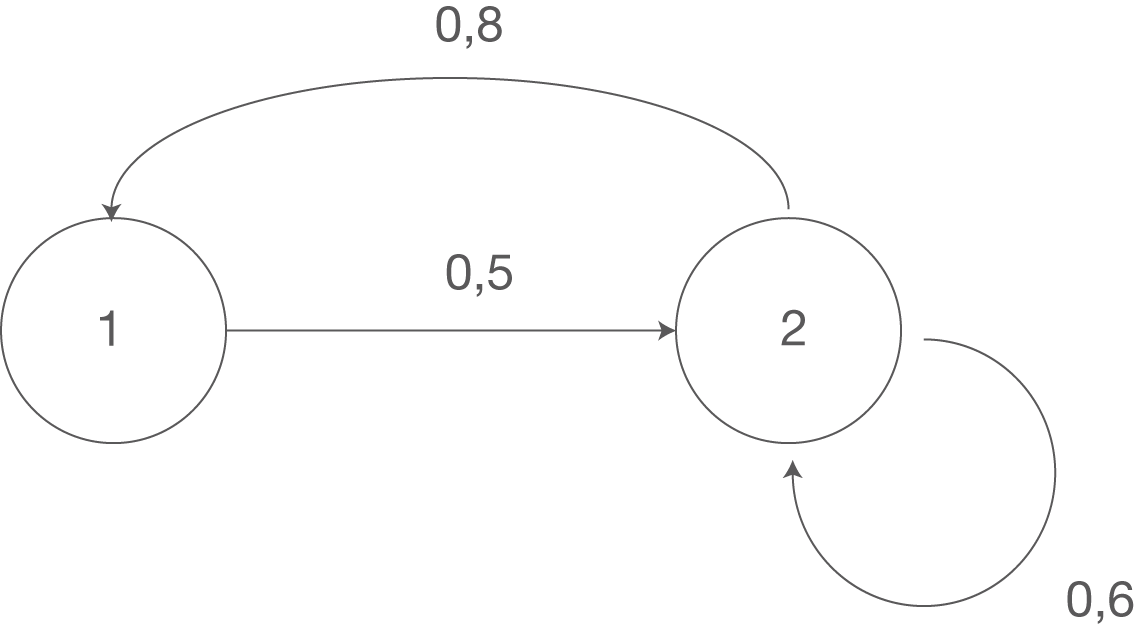

- Geben sie dazu eine Übergangsmatrix M an.
- Beschreiben Sie anhand des Übergangsgraphen, nach welchen Modellannahmen die Entwicklung der Population dieser anderen Vogelart im Vergleich zur bisher betrachteten Seevogelart abläuft.
(4P + 5P)
a) (1)  Verteilung der Vögel nach einem und zwei Jahren berechnen
Deine Aufgabe ist es hier, die Verteilung der Vögel nach einem und nach zwei Jahren zu berechnen, wobei dir die aktuelle Verteilung gegeben ist mit:
Verteilung der Vögel nach einem und zwei Jahren berechnen
Deine Aufgabe ist es hier, die Verteilung der Vögel nach einem und nach zwei Jahren zu berechnen, wobei dir die aktuelle Verteilung gegeben ist mit:
 Die Übergangsmatrix ist dir ebenfalls gegeben mit
Die Übergangsmatrix ist dir ebenfalls gegeben mit  Hierbei bietet sich die folgende Formel an, um die Verteilung zum Zeitpunkt
Hierbei bietet sich die folgende Formel an, um die Verteilung zum Zeitpunkt  zu berechnen:
zu berechnen:
 Dort kannst du nun
Dort kannst du nun  ,
,  für
für  und
und  bzw
bzw  einsetzen und erhältst so die Verteilung der Vögel nach ein bzw. zwei Jahren.
Dabei kannst du deinen GTR zu Hilfe nehmen oder auch handschriftlich rechnen.
einsetzen und erhältst so die Verteilung der Vögel nach ein bzw. zwei Jahren.
Dabei kannst du deinen GTR zu Hilfe nehmen oder auch handschriftlich rechnen.
 Lösungsweg A: Handschriftlich
Hierbei kannst du zunächst die Verteilung nach einem Jahr berechnen und diese zur Berechnung der Verteilung im zweiten Jahr wieder verwenden:
Lösungsweg A: Handschriftlich
Hierbei kannst du zunächst die Verteilung nach einem Jahr berechnen und diese zur Berechnung der Verteilung im zweiten Jahr wieder verwenden:
 Nach einem Jahr sind
Nach einem Jahr sind  Jungvögel,
Jungvögel,  Vögel im 2. Lebensjahr und
Vögel im 2. Lebensjahr und  Altvögel vorhanden.
Nun kennst du
Altvögel vorhanden.
Nun kennst du  und kannst damit
und kannst damit  berechnen:
berechnen:
 Nach zwei Jahren sind
Nach zwei Jahren sind  Jungvögel,
Jungvögel,  Vögel im zweiten Lebensjahr und
Vögel im zweiten Lebensjahr und  Altvögel vorhanden.
Altvögel vorhanden.
 Lösungsweg B: GTR
Mit dem GTR kannst du hier am besten arbeiten, indem du zunächst die Übergangsmatrix
Lösungsweg B: GTR
Mit dem GTR kannst du hier am besten arbeiten, indem du zunächst die Übergangsmatrix  unter der Bezeichnung
unter der Bezeichnung  speicherst. Dies kannst du im Rechenmenü tun. Wähle dazu unter
speicherst. Dies kannst du im Rechenmenü tun. Wähle dazu unter
 aus. Anschließend musst du zunächst die Dimension der Matrix (3 x 3) und anschließend die Matrixeinträge eingeben. Verlasse das Matrixmenü anschließend wieder. Das gleiche kannst du mit dem Verteilungsvektor
aus. Anschließend musst du zunächst die Dimension der Matrix (3 x 3) und anschließend die Matrixeinträge eingeben. Verlasse das Matrixmenü anschließend wieder. Das gleiche kannst du mit dem Verteilungsvektor  tun und ihn unter
tun und ihn unter  abspeichern. Dieser hat die Dimension 3 x 1.
abspeichern. Dieser hat die Dimension 3 x 1.
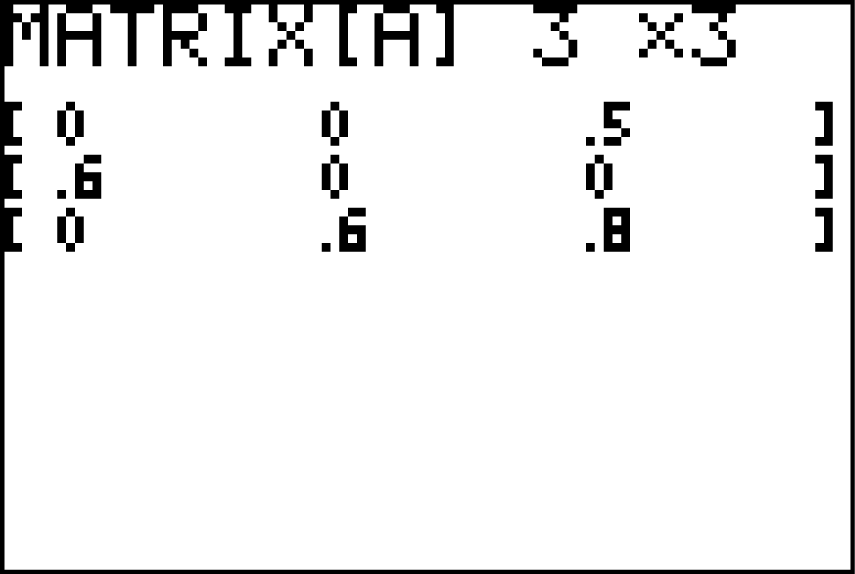
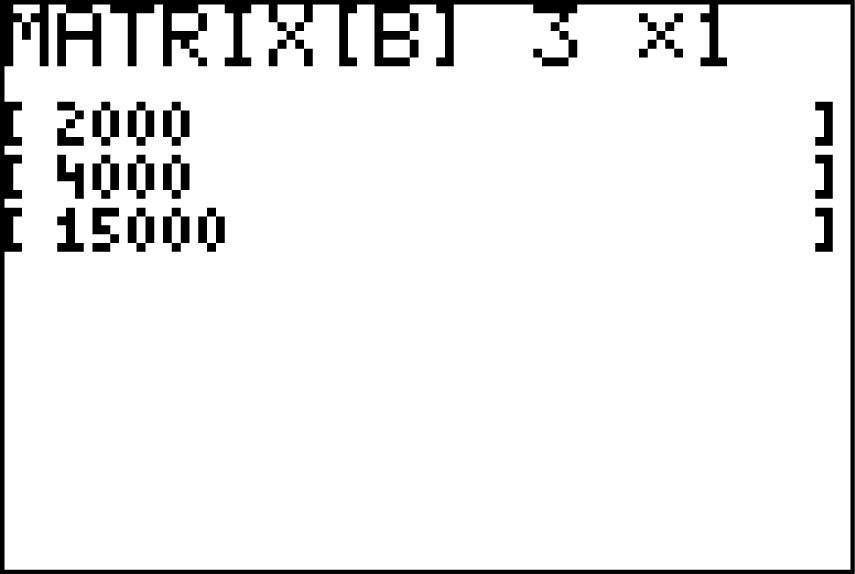 Dann kannst du anschließend
Dann kannst du anschließend  berechnen, indem du die Matrix bzw. den Vektor wieder aufrufst. Den Befehl um eine Matrix abzurufen findest du unter:
berechnen, indem du die Matrix bzw. den Vektor wieder aufrufst. Den Befehl um eine Matrix abzurufen findest du unter:

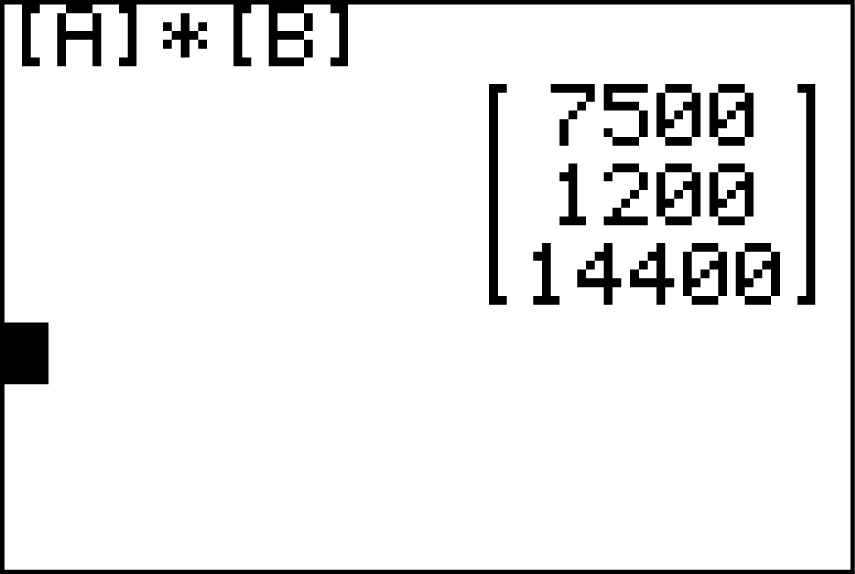 Nach einem Jahr sind
Nach einem Jahr sind  Jungvögel,
Jungvögel,  Vögel im 2. Lebensjahr und
Vögel im 2. Lebensjahr und  Altvögel vorhanden.
Genauso kannst du nun auch die Verteilung nach zwei Jahren berechnen, indem du den Verteilungsvektor
Altvögel vorhanden.
Genauso kannst du nun auch die Verteilung nach zwei Jahren berechnen, indem du den Verteilungsvektor  als C speicherst:
als C speicherst:

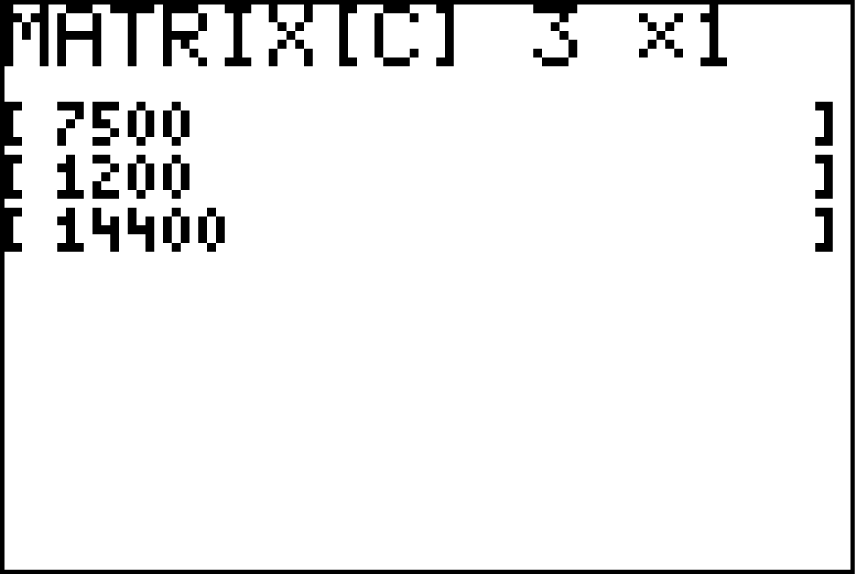
 Nach zwei Jahren sind
Nach zwei Jahren sind  Jungvögel,
Jungvögel,  Vögel im zweiten Lebensjahr und
Vögel im zweiten Lebensjahr und  Altvögel vorhanden.
(2)
Altvögel vorhanden.
(2)  Verteilung für das Vorjahr berechnen
Nun sollst du die Verteilung für das Vorjahr berechnen. Also die Anzahl der verschiedenen Altersgruppen der Vögel zum Zeitpunkt
Verteilung für das Vorjahr berechnen
Nun sollst du die Verteilung für das Vorjahr berechnen. Also die Anzahl der verschiedenen Altersgruppen der Vögel zum Zeitpunkt  . Hier kannst du wieder die Formel von oben anwenden, und zwar kennst du in diesem Fall den Verteilungsvektor
. Hier kannst du wieder die Formel von oben anwenden, und zwar kennst du in diesem Fall den Verteilungsvektor  und die Übergangsmatrix
und die Übergangsmatrix  und du suchst den Verteilungsvektor
und du suchst den Verteilungsvektor
 ,
das heißt die Verteilung, sodass daraus ein Jahr später die Verteilung
,
das heißt die Verteilung, sodass daraus ein Jahr später die Verteilung  entsteht.
Insgesamt suchst du also den Verteilungsvektor
entsteht.
Insgesamt suchst du also den Verteilungsvektor  , der die folgende Gleichung erfüllt:
, der die folgende Gleichung erfüllt:
 Setzt du dort die Informationen ein, so kannst du aus dieser Gleichung ein
lineares Gleichungssystem in Abhängigkeit von
Setzt du dort die Informationen ein, so kannst du aus dieser Gleichung ein
lineares Gleichungssystem in Abhängigkeit von  ,
,  und
und  gewinnen, welches du anschließend entweder mit dem GTR oder per Hand lösen kannst.
1. Schritt: Lineares Gleichungssystem aufstellen
Setzt du
gewinnen, welches du anschließend entweder mit dem GTR oder per Hand lösen kannst.
1. Schritt: Lineares Gleichungssystem aufstellen
Setzt du  und
und  in die Gleichung ein, so erhältst du folgende Gleichung:
in die Gleichung ein, so erhältst du folgende Gleichung:
 Dort kannst du nun jede „Zeile“ einzeln ablesen. Dann erhältst du das folgende lineare Gleichungssystem:
Dort kannst du nun jede „Zeile“ einzeln ablesen. Dann erhältst du das folgende lineare Gleichungssystem:
 2. Schritt: Gleichungssystem lösen
Hier hast du auch wieder zwei Möglichkeiten, entweder du löst das LGS mit Hilfe des GTR oder handschriftlich.
2. Schritt: Gleichungssystem lösen
Hier hast du auch wieder zwei Möglichkeiten, entweder du löst das LGS mit Hilfe des GTR oder handschriftlich.
 Lösungsweg A: Handschriftlich
Du kannst schnell erkennen, dass die erste und zweite Gleichung des LGS jeweils von nur einer Variablen abhängen. Außerdem weißt du, dass du aus einer Gleichung mit einer Variablen die Lösung für die Variablen direkt bestimmen kannst.
Du kannst hier also wie folgt vorgehen:
Lösungsweg A: Handschriftlich
Du kannst schnell erkennen, dass die erste und zweite Gleichung des LGS jeweils von nur einer Variablen abhängen. Außerdem weißt du, dass du aus einer Gleichung mit einer Variablen die Lösung für die Variablen direkt bestimmen kannst.
Du kannst hier also wie folgt vorgehen:
 Aus der zweiten Gleichung erhältst du:
Aus der zweiten Gleichung erhältst du:
 Setzt du dies nun in (3) ein, so kannst du nach
Setzt du dies nun in (3) ein, so kannst du nach  auflösen:
auflösen:
 Aus dem Modell ergäbe sich die folgende Verteilung für das Vorjahr:
Es waren ca. 6.667 Jungvögel, 19.667 Vögel im 2. Lebensjahr und 4.000 Altvögel vorhanden.
Aus dem Modell ergäbe sich die folgende Verteilung für das Vorjahr:
Es waren ca. 6.667 Jungvögel, 19.667 Vögel im 2. Lebensjahr und 4.000 Altvögel vorhanden.
 Lösungsweg B: GTR
Mit dem GTR kannst du das LGS lösen, indem du die Koeffizienten als Einträge einer Matrix auffasst. Es ergibt sich die folgende Matrix:
Lösungsweg B: GTR
Mit dem GTR kannst du das LGS lösen, indem du die Koeffizienten als Einträge einer Matrix auffasst. Es ergibt sich die folgende Matrix:
 Diese kannst du wie zuvor zunächst eingeben und abspeichern. Verlasse das Matrixmenü anschließend wieder.
Dann kannst du die Matrix
Diese kannst du wie zuvor zunächst eingeben und abspeichern. Verlasse das Matrixmenü anschließend wieder.
Dann kannst du die Matrix  mit dem rref-Befehl so umformen, dass sie dir die Lösungen anzeigt. Den Befehl findest du unter
mit dem rref-Befehl so umformen, dass sie dir die Lösungen anzeigt. Den Befehl findest du unter
 in der Klammer hinter dem Befehl wieder so auf wie zuvor.
Bestätigst du anschließend mit ENTER, so erhältst du die folgende Matrix als Ergebnis:
in der Klammer hinter dem Befehl wieder so auf wie zuvor.
Bestätigst du anschließend mit ENTER, so erhältst du die folgende Matrix als Ergebnis:

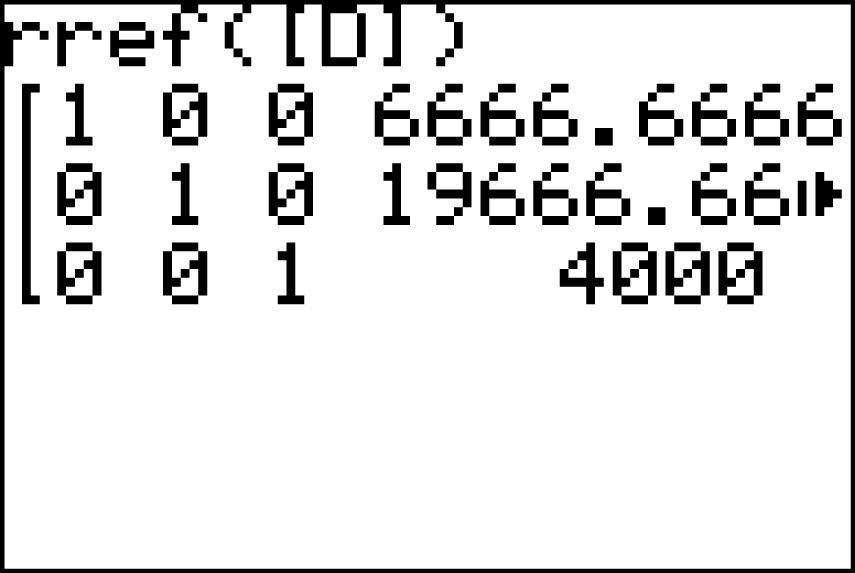 Daraus kannst du das Ergebnis ablesen und erhältst:
Daraus kannst du das Ergebnis ablesen und erhältst:
 ,
,  ,
,  Aus dem Modell ergäbe sich die folgende Verteilung für das Vorjahr:
Es waren ca. 6.667 Jungvögel, 19.667 Vögel im 2. Lebensjahr und 4.000 Altvögel vorhanden.
(3)
Aus dem Modell ergäbe sich die folgende Verteilung für das Vorjahr:
Es waren ca. 6.667 Jungvögel, 19.667 Vögel im 2. Lebensjahr und 4.000 Altvögel vorhanden.
(3)  Nullwerte der Matrix erklären
In diesem Aufgabenteil, sollst du für jedes Element der Matrix
Nullwerte der Matrix erklären
In diesem Aufgabenteil, sollst du für jedes Element der Matrix  , das den Wert Null hat, erklären, warum es eben diesen Wert hat. Am besten kannst du dabei schrittweise für jedes Element einzeln vorgehen.
Die folgenden Elemente der Matrix
, das den Wert Null hat, erklären, warum es eben diesen Wert hat. Am besten kannst du dabei schrittweise für jedes Element einzeln vorgehen.
Die folgenden Elemente der Matrix  haben den Wert Null:
haben den Wert Null:
 gibt dabei den Anteil der Vögel an, die im nächsten Jahr von Altersgruppe
gibt dabei den Anteil der Vögel an, die im nächsten Jahr von Altersgruppe  in Altersgruppe
in Altersgruppe  übergehen. Bei den Altvögeln bedeutet
übergehen. Bei den Altvögeln bedeutet  beispielsweise, dass jeder Altvogel im Schnitt pro Jahr
beispielsweise, dass jeder Altvogel im Schnitt pro Jahr  Nachkommen hat.
Erklärung für
Nachkommen hat.
Erklärung für  Das erste Element
Das erste Element  beschreibt den Anteil der Vögel, die nach einem Jahr vom Stadium
beschreibt den Anteil der Vögel, die nach einem Jahr vom Stadium  immer noch im Stadium
immer noch im Stadium  bleiben. Da
bleiben. Da  aber das Stadium der Vögel im ersten Lebensjahr bezeichnet, ist dieser Wert Null, weil ein Vogel nicht zwei Jahre hintereinander im 1. Lebensjahr sein kann.
Erklärung für
aber das Stadium der Vögel im ersten Lebensjahr bezeichnet, ist dieser Wert Null, weil ein Vogel nicht zwei Jahre hintereinander im 1. Lebensjahr sein kann.
Erklärung für 
 beschreibt den Anteil der Vögel, die von der Altersgruppe
beschreibt den Anteil der Vögel, die von der Altersgruppe  in die Altersgruppe
in die Altersgruppe  übergehen. Für einen solchen Übergang müsste folgendes passieren:
übergehen. Für einen solchen Übergang müsste folgendes passieren:

 hat aus ähnlichen Gründen den Wert Null, wie
hat aus ähnlichen Gründen den Wert Null, wie  . Nach einem Jahr ist jeder Vogel entweder ein Jahr älter oder gestorben. Ist er vorher in Altersgruppe
. Nach einem Jahr ist jeder Vogel entweder ein Jahr älter oder gestorben. Ist er vorher in Altersgruppe  , also im zweiten Lebensjahr, so kann er im nächsten Jahr nicht noch einmal in Altergruppe
, also im zweiten Lebensjahr, so kann er im nächsten Jahr nicht noch einmal in Altergruppe  sein. Daher hat
sein. Daher hat  den Wert Null.
Erklärung für
den Wert Null.
Erklärung für  Hierbei verläuft die Erklärung analog zu
Hierbei verläuft die Erklärung analog zu  .
.  beschreibt den Anteil der Vögel, die von Altersgruppe
beschreibt den Anteil der Vögel, die von Altersgruppe  nach einem Jahr zurück in Altersgruppe
nach einem Jahr zurück in Altersgruppe  übergeht. Dies würde aber bedeuten, dass ein Vogel vom dritten Lebensjahr, ein Jahr später im 2. Lebensjahr wäre. Dies ist unmöglich. Nachkommen, die nach einem Jahr bereits das zweite Lebensjahr erreicht haben, kann ein Altvogel auch nicht produzieren. Daher hat
übergeht. Dies würde aber bedeuten, dass ein Vogel vom dritten Lebensjahr, ein Jahr später im 2. Lebensjahr wäre. Dies ist unmöglich. Nachkommen, die nach einem Jahr bereits das zweite Lebensjahr erreicht haben, kann ein Altvogel auch nicht produzieren. Daher hat  den Wert Null.
Erklärung für
den Wert Null.
Erklärung für 
 beschreibt den Anteil der Vögel aus Altersgruppe
beschreibt den Anteil der Vögel aus Altersgruppe  , die nach einem Jahr Altersgruppe
, die nach einem Jahr Altersgruppe  angehören. Da dies aber bedeuten würde, dass ein Vogel das zweite Lebensjahr überspringen würde, ist dies unmöglich. Daher ist
angehören. Da dies aber bedeuten würde, dass ein Vogel das zweite Lebensjahr überspringen würde, ist dies unmöglich. Daher ist  .
.
2ND 
 (MATRIX)
(MATRIX)  EDIT
EDIT
die Bezeichnung 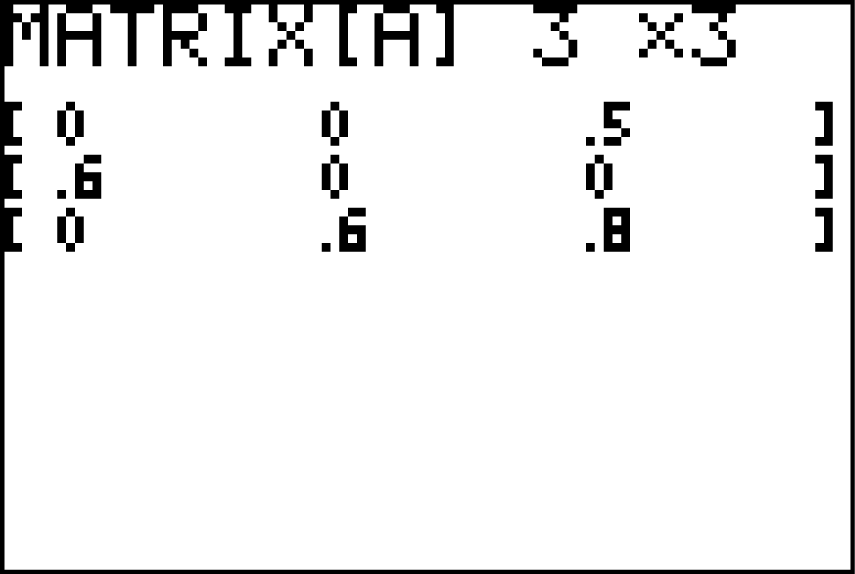
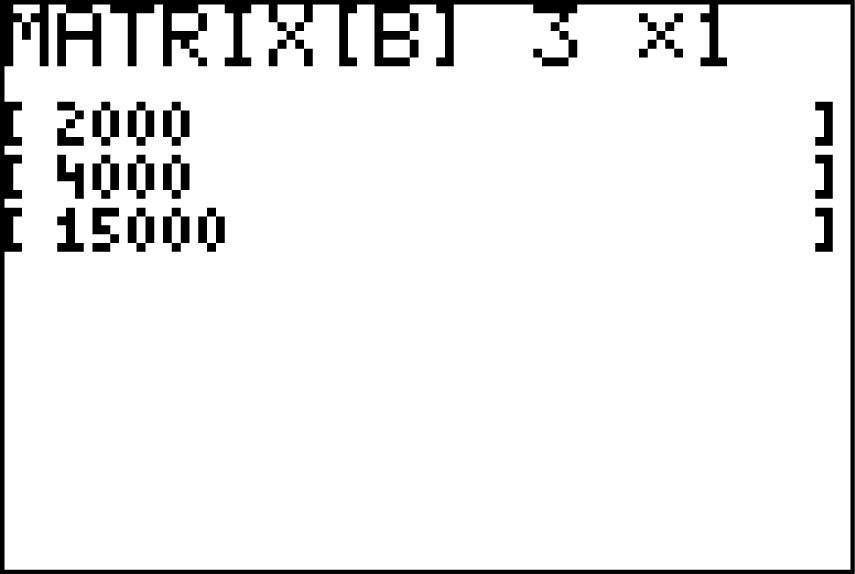
2ND 
 (MATRIX)
(MATRIX)  NAMES
NAMES

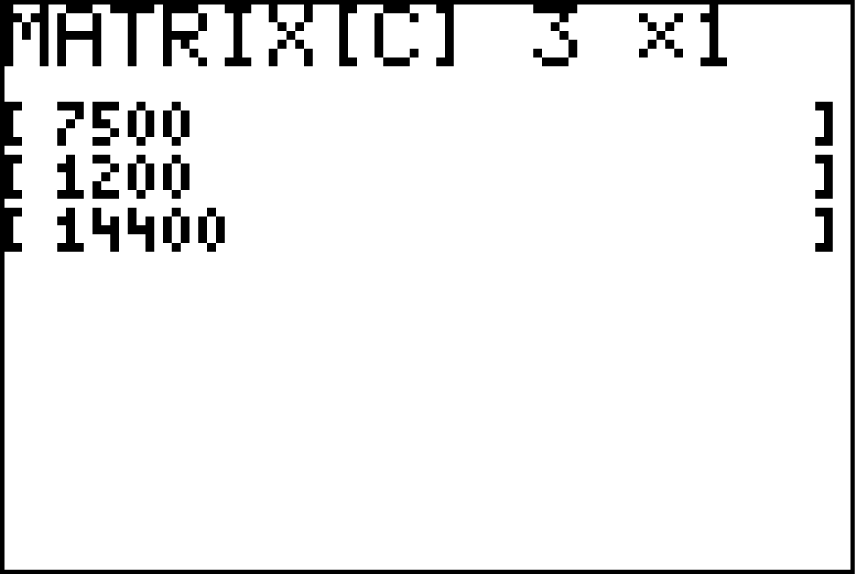

- Löse (1) nach
und bestimme so die Lösung für
- Löse (2) nach
und bestimme so die Lösung für
- Setze die Lösungen aus den ersten beiden Schritten in (3) ein und bestimme die Lösung für
durch Umformen von (3)
2ND 
 (MATRIX)
(MATRIX)  MATH
MATH  B: rref(
B: rref(
Rufe dazu die Matrix 
- Ein Vogel, der im zweiten Lebensjahr ist, ist ein Jahr später wieder im ersten Lebensjahr oder
- Ein Vogel im zweiten Lebensjahr zeugt Nachkommen
b) (1)  Auf stationäre Verteilungen untersuchen
Hier ist es deine Aufgabe, zu untersuchen, ob es eine von
Auf stationäre Verteilungen untersuchen
Hier ist es deine Aufgabe, zu untersuchen, ob es eine von  verschiedene stationäre Verteilung gibt. Eine stationäre Verteilung ist eine Verteilung
verschiedene stationäre Verteilung gibt. Eine stationäre Verteilung ist eine Verteilung  , sodass
, sodass  usw. gilt. Das bedeutet,
usw. gilt. Das bedeutet,  muss die folgende Gleichung erfüllen:
muss die folgende Gleichung erfüllen:
 Aus dieser Gleichung ergibt sich mit
Aus dieser Gleichung ergibt sich mit  wieder ein lineares Gleichungssystem in Abhängigkeit von
wieder ein lineares Gleichungssystem in Abhängigkeit von  ,
,  und
und  . Dieses kannst du dann wieder mit dem GTR oder auch handschriftlich lösen.
1. Schritt: Lineares Gleichungssystem aufstellen
Das lineare Gleichungssystem kannst du wieder wie in Aufgabenteil a) (2) aufstellen, indem du die Matrix und den Vektor miteinander multiplizierst und anschließend jede „Zeile“ einzeln abliest:
. Dieses kannst du dann wieder mit dem GTR oder auch handschriftlich lösen.
1. Schritt: Lineares Gleichungssystem aufstellen
Das lineare Gleichungssystem kannst du wieder wie in Aufgabenteil a) (2) aufstellen, indem du die Matrix und den Vektor miteinander multiplizierst und anschließend jede „Zeile“ einzeln abliest:
 Daraus ergibt sich dann das folgende LGS:
Daraus ergibt sich dann das folgende LGS:
 2. Schritt: Gleichungssystem lösen
Das LGS kannst du nun handschriftlich oder mit dem GTR lösen.
2. Schritt: Gleichungssystem lösen
Das LGS kannst du nun handschriftlich oder mit dem GTR lösen.
 Lösungsweg A: Handschriftlich
Hier kannst du mit dem Einsetzungsverfahren arbeiten. Wie du siehst, hast du
Lösungsweg A: Handschriftlich
Hier kannst du mit dem Einsetzungsverfahren arbeiten. Wie du siehst, hast du  in Abhängigkeit von
in Abhängigkeit von  dargestellt und
dargestellt und  in Abhängigkeit von
in Abhängigkeit von  . Setzt du nun
. Setzt du nun  in (2) ein, so erhältst du
in (2) ein, so erhältst du  ebenfalls in Abhängigkeit von
ebenfalls in Abhängigkeit von  . Dann kannst du diese Darstellungsweisen von
. Dann kannst du diese Darstellungsweisen von  und
und  in (3) einsetzen, die dann nur noch von
in (3) einsetzen, die dann nur noch von  abhängt. So kannst du eine Lösung für
abhängt. So kannst du eine Lösung für  bestimmen und anschließend die Lösungen für
bestimmen und anschließend die Lösungen für  und
und  .
.
 Setzt du nun
Setzt du nun  und
und  in (3) ein, so erhältst du:
in (3) ein, so erhältst du:
 Mit
Mit  ergibt sich für
ergibt sich für  und
und  :
:

 Damit wäre also
Damit wäre also  , was der Voraussetzung widerspricht.
Es existiert keine stationäre Verteilung außer
, was der Voraussetzung widerspricht.
Es existiert keine stationäre Verteilung außer  .
.
 Lösungsweg B: GTR
Um das LGS wie zuvor mit dem GTR zu lösen, musst du zunächst alle
Lösungsweg B: GTR
Um das LGS wie zuvor mit dem GTR zu lösen, musst du zunächst alle  auf eine Seite bringen. Dann wird aus
auf eine Seite bringen. Dann wird aus

 Fasst du nun die Koeffizienten wieder als Einträge einer Matrix auf und wendest auf diese Matrix den rref-Befehl (diesen kennst du bereits aus Aufgabenteil a) ) des GTR an, so erhältst du:
Fasst du nun die Koeffizienten wieder als Einträge einer Matrix auf und wendest auf diese Matrix den rref-Befehl (diesen kennst du bereits aus Aufgabenteil a) ) des GTR an, so erhältst du:

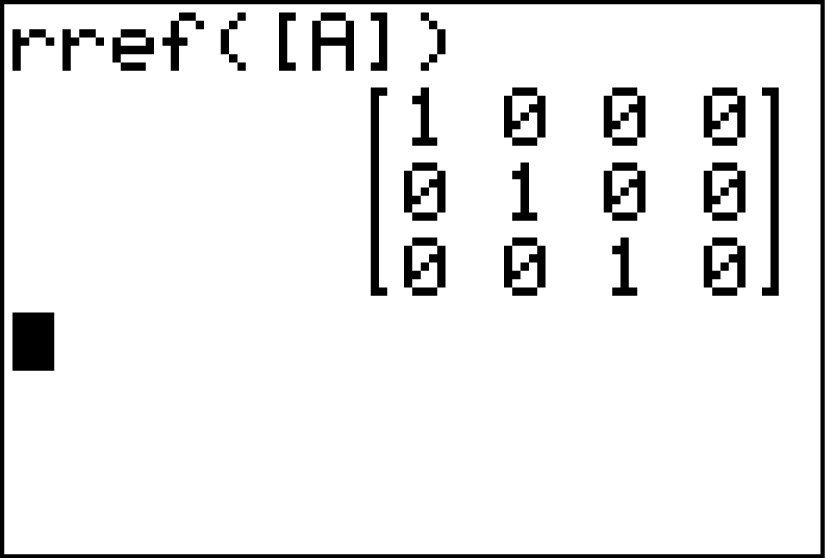 Damit existiert keine stationäre Verteilung außer
Damit existiert keine stationäre Verteilung außer  .
(2)
.
(2)  Prozentsatz berechnen
Nun sollst du den Prozentsatz
Prozentsatz berechnen
Nun sollst du den Prozentsatz  näherungsweise berechnen, um den sich die Gesamtpopulation der Vögel jährlich verkleinert. Du hast dazu die Gesamtpopulation
näherungsweise berechnen, um den sich die Gesamtpopulation der Vögel jährlich verkleinert. Du hast dazu die Gesamtpopulation  zu zwei Zeitpunkten
zu zwei Zeitpunkten  und
und  gegeben:
gegeben:

 Wenn sich die Gesamtpopulation
Wenn sich die Gesamtpopulation  innerhalb eines Jahres um den Prozentsatz
innerhalb eines Jahres um den Prozentsatz  verkleinert, so bleibt ein Anteil von
verkleinert, so bleibt ein Anteil von  der Population erhalten. Also gilt aufgrund der Regeln der Prozentrechnung:
der Population erhalten. Also gilt aufgrund der Regeln der Prozentrechnung:
 Du kennst nun aber nicht zwei Werte, die nur ein Jahr auseinander liegen, sondern zwei Werte, die 10 Jahre auseinander liegen. Du suchst also eine Formel für
Du kennst nun aber nicht zwei Werte, die nur ein Jahr auseinander liegen, sondern zwei Werte, die 10 Jahre auseinander liegen. Du suchst also eine Formel für  in Abhängigkeit von
in Abhängigkeit von  . Aus der obigen Formel kannst du solch eine Formel herleiten und anschließend mit Hilfe der gegebenen Werte eine Gleichung in Abhängigkeit von
. Aus der obigen Formel kannst du solch eine Formel herleiten und anschließend mit Hilfe der gegebenen Werte eine Gleichung in Abhängigkeit von  aufstellen und so anschließend
aufstellen und so anschließend  berechnen.
1. Schritt: Gleichung aufstellen
Du weißt, dass
berechnen.
1. Schritt: Gleichung aufstellen
Du weißt, dass  gilt. Das gleiche kannst du auch für
gilt. Das gleiche kannst du auch für  formulieren:
formulieren:
 Dort kannst du nun wieder die Formel für
Dort kannst du nun wieder die Formel für  einsetzen und erhältst:
einsetzen und erhältst:
 Du kannst folgendes erkennen: Setzt du dies immer weiter fort, bis du
Du kannst folgendes erkennen: Setzt du dies immer weiter fort, bis du  erhältst so kommt jedes mal einmal der Faktor
erhältst so kommt jedes mal einmal der Faktor  hinzu:
hinzu:
 2. Schritt: Gleichung aufstellen und lösen
Setzt du nun die beiden Werte in die Formel ein, so erhältst du die folgende Gleichung:
2. Schritt: Gleichung aufstellen und lösen
Setzt du nun die beiden Werte in die Formel ein, so erhältst du die folgende Gleichung:
 Diese Gleichung kannst du nun entweder handschriftlich oder auch mit Hilfe des GTR lösen.
Diese Gleichung kannst du nun entweder handschriftlich oder auch mit Hilfe des GTR lösen.
 Lösungsweg A: Handschriftlich
Lösungsweg A: Handschriftlich
![\(\begin{array}{rll}
15.422 &=&(1-p)^{10} \cdot 17.870&\scriptsize{ \mid\; : 17.870 }\\
0,86301&\approx&(1-p)^{10}&\scriptsize{ \mid\; \sqrt[10]{\quad}}\\
0,98538&\approx&1-p&\scriptsize{ \mid\; -1}\\
-0,01462&\approx&-p&\scriptsize{ \mid\; \cdot (-1)}\\
0,01462&\approx&p\\
1,462\,\%&\approx&p\\
\end{array}\)](https://mathjax.schullv.de/c2640585ef082f79c28385a8d573eaa748ed90db3171300cbc7bd9b70bc8896d?color=5a5a5a) Die Gesamtpopulation der Seevögel reduziert sich jährlich um einen Prozentsatz von
Die Gesamtpopulation der Seevögel reduziert sich jährlich um einen Prozentsatz von  .
.
 Lösungsweg B: GTR
Mit dem GTR kannst du die Gleichung lösen, indem du diese in ein Nullstellenproblem umformst:
Lösungsweg B: GTR
Mit dem GTR kannst du die Gleichung lösen, indem du diese in ein Nullstellenproblem umformst:
 Den rechten Teil der Gleichung kannst du nun als Funktionsterm einer Funktion
Den rechten Teil der Gleichung kannst du nun als Funktionsterm einer Funktion  in Abhängigkeit von
in Abhängigkeit von  auffassen. Bestimmst du mit Hilfe des Graph-Menüs des GTR nun wie zuvor die Nullstellen der Funktion
auffassen. Bestimmst du mit Hilfe des Graph-Menüs des GTR nun wie zuvor die Nullstellen der Funktion  , so erhältst du die Lösung:
, so erhältst du die Lösung:  .
.
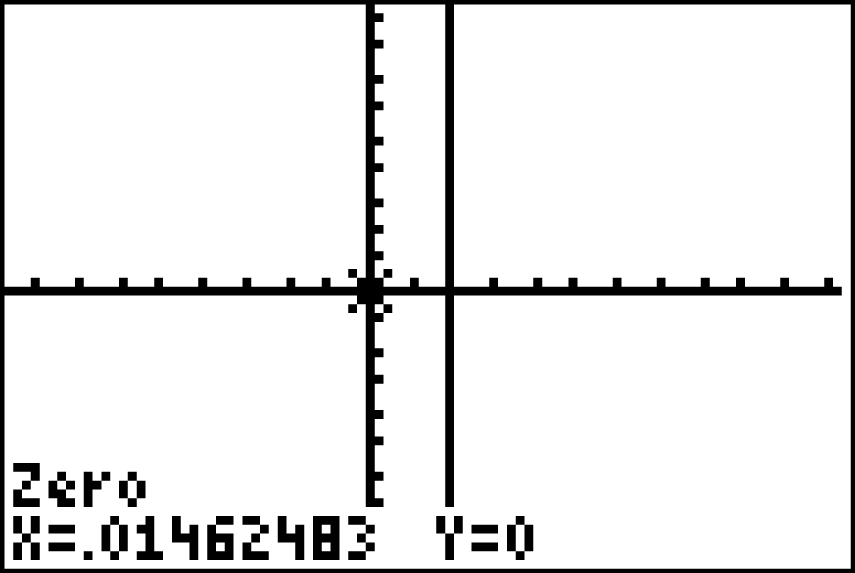 Die Gesamtpopulation der Seevögel reduziert sich jährlich um einen Prozentsatz von
Die Gesamtpopulation der Seevögel reduziert sich jährlich um einen Prozentsatz von  .
(3)
.
(3)  Anzahl der Jahre ermitteln, in denen sich die Population halbiert
In dieser Aufgabe sollst du nun die Anzahl der Jahre ermitteln, nach denen sich die Population halbiert. Das heißt, du sollst
Anzahl der Jahre ermitteln, in denen sich die Population halbiert
In dieser Aufgabe sollst du nun die Anzahl der Jahre ermitteln, nach denen sich die Population halbiert. Das heißt, du sollst  finden, sodass die folgende Gleichung gilt:
finden, sodass die folgende Gleichung gilt:
 Aus dem vorherigen Aufgabenteil weißt du, dass du
Aus dem vorherigen Aufgabenteil weißt du, dass du  auf folgende Weise berechnen kannst:
auf folgende Weise berechnen kannst:
 }
Da du
}
Da du  kennst, kannst du dies in die obere Gleichung einsetzen und erhältst so eine Gleichung in Abhängigkeit von
kennst, kannst du dies in die obere Gleichung einsetzen und erhältst so eine Gleichung in Abhängigkeit von  . Diese kannst du dann nach
. Diese kannst du dann nach  lösen.
lösen.
 Diese Gleichung kannst du nun ebenfalls wieder handschriftlich oder mit dem GTR lösen.
Diese Gleichung kannst du nun ebenfalls wieder handschriftlich oder mit dem GTR lösen.
 Lösungsweg A: Handschriftlich
Handschriftlich kannst du die Gleichung nun weiter nach
Lösungsweg A: Handschriftlich
Handschriftlich kannst du die Gleichung nun weiter nach  umformen, indem du einen Logarithmus anwendest, beispielsweise den Logarithmus zur Basis
umformen, indem du einen Logarithmus anwendest, beispielsweise den Logarithmus zur Basis  . Dann erhältst du:
. Dann erhältst du:
 Nach etwa
Nach etwa  Jahren halbiert sich die Population jeweils.
Jahren halbiert sich die Population jeweils.
 Lösungsweg B: GTR
Um die Gleichung mit Hilfe des GTR zu lösen, kannst du die Gleichung wieder in ein Nullstellenproblem umformen:
Lösungsweg B: GTR
Um die Gleichung mit Hilfe des GTR zu lösen, kannst du die Gleichung wieder in ein Nullstellenproblem umformen:
 Nun kannst du wie zuvor die Nullstellen der Funktion
Nun kannst du wie zuvor die Nullstellen der Funktion  mit
mit  bestimmen und erhältst:
bestimmen und erhältst:

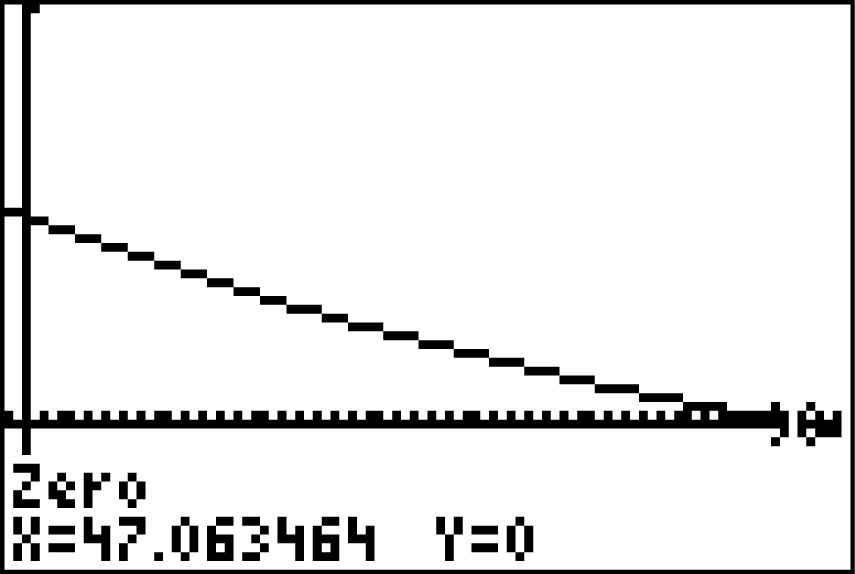 Nach etwa
Nach etwa  Jahren halbiert sich die Population jeweils.
(4)
Jahren halbiert sich die Population jeweils.
(4)  Zeigen, dass die angegebene Verteilung stationär ist
Du sollst zeigen, dass die Verteilung
Zeigen, dass die angegebene Verteilung stationär ist
Du sollst zeigen, dass die Verteilung  für jede positive ganze Zahl
für jede positive ganze Zahl  eine stationäre Verteilung ist. Was eine stationäre Verteilung ist, weißt du bereits aus Aufgabenteil b) (1). Da sich nun aber der Bruterfolg der Seevögel durch Schutzmaßnahmen verbessert hat, musst du hier die Matrix zunächst anpassen. Wie du weißt, beschreibt der Eintrag
eine stationäre Verteilung ist. Was eine stationäre Verteilung ist, weißt du bereits aus Aufgabenteil b) (1). Da sich nun aber der Bruterfolg der Seevögel durch Schutzmaßnahmen verbessert hat, musst du hier die Matrix zunächst anpassen. Wie du weißt, beschreibt der Eintrag  die Anzahl der Nachkommen pro Jahr pro Altvogel. Dies ist also der Eintrag, den du ersetzen musst. Damit ergibt sich die „neue“ Matrix mit:
die Anzahl der Nachkommen pro Jahr pro Altvogel. Dies ist also der Eintrag, den du ersetzen musst. Damit ergibt sich die „neue“ Matrix mit:
 Um nun zu zeigen, dass
Um nun zu zeigen, dass  eine stationäre Verteilung ist, kannst du die Gleichung aus Aufgabenteil b) (1) anwenden. Damit
eine stationäre Verteilung ist, kannst du die Gleichung aus Aufgabenteil b) (1) anwenden. Damit  eine stationäre Verteilung zu der neuen Übergangsmatrix ist, muss gelten:
eine stationäre Verteilung zu der neuen Übergangsmatrix ist, muss gelten:
 Setzt du dort die Matrix und die Verteilung ein, so kannst du nachrechnen, ob diese Gleichung stimmt:
Setzt du dort die Matrix und die Verteilung ein, so kannst du nachrechnen, ob diese Gleichung stimmt:
 Diese Gleichung stimmt, und damit ist
Diese Gleichung stimmt, und damit ist  eine stationäre Verteilung für alle positiven ganzen Zahlen
eine stationäre Verteilung für alle positiven ganzen Zahlen  .
(5)
.
(5)  Prozentuale Anteile berechnen
Hier ist es deine Aufgabe, für eine der stationären Verteilung aus (4) die prozentualen Anteile der einzelnen Altersgruppen an der Gesamtpopulation zu berechnen. Das bedeutet, du sollst nun für ein
Prozentuale Anteile berechnen
Hier ist es deine Aufgabe, für eine der stationären Verteilung aus (4) die prozentualen Anteile der einzelnen Altersgruppen an der Gesamtpopulation zu berechnen. Das bedeutet, du sollst nun für ein  deiner Wahl berechnen, wie viel Prozent der Vögel Jungvögel, Vögel im 2. Lebensjahr oder Altvögel sind.
Dabei kannst du so vorgehen:
deiner Wahl berechnen, wie viel Prozent der Vögel Jungvögel, Vögel im 2. Lebensjahr oder Altvögel sind.
Dabei kannst du so vorgehen:
 der Altersgruppe
der Altersgruppe  an der Gesamtpopulation
an der Gesamtpopulation  :
:
 Dabei ist
Dabei ist  der Verteilungsvektor der stationären Verteilung, die du betrachtest.
1. Schritt: Verteilung und Gesamtpopulation berechnen
Wählst du zum Beispiel
der Verteilungsvektor der stationären Verteilung, die du betrachtest.
1. Schritt: Verteilung und Gesamtpopulation berechnen
Wählst du zum Beispiel  , dann ergibt sich der folgende Verteilungsvektor:
, dann ergibt sich der folgende Verteilungsvektor:
 Damit ist:
Damit ist:  ,
,  und
und  .
Die Gesamtpopulation ist dann also:
.
Die Gesamtpopulation ist dann also:  .
2. Schritt: Anteile der Altersgruppen berechnen
Nun kennst du alle Werte, die du benötigst und kannst diese nacheinander in die Formel einsetzen, um
.
2. Schritt: Anteile der Altersgruppen berechnen
Nun kennst du alle Werte, die du benötigst und kannst diese nacheinander in die Formel einsetzen, um  ,
,  und
und  zu berechnen:
zu berechnen:


 Für
Für  und die stationäre Verteilung
und die stationäre Verteilung  hat Altersgruppe 1 einen prozentualen Anteil an der Gesamtpopulation von ca.
hat Altersgruppe 1 einen prozentualen Anteil an der Gesamtpopulation von ca.  , Altersgruppe 2 hat einen Anteil von ca.
, Altersgruppe 2 hat einen Anteil von ca.  und Altersgruppe 3 einen Anteil von ca.
und Altersgruppe 3 einen Anteil von ca.  an der Gesamtpopulation.
an der Gesamtpopulation.
 Zeigen, dass sich für beliebiges
Zeigen, dass sich für beliebiges  die gleichen Anteile ergeben
Im vorherigen Aufgabenteil hast du bereits die prozentualen Anteile der einzelnen Altersgruppen für eine konkrete stationäre Verteilung berechnet. Nun sollst du zeigen, dass diese Anteile für jedes
die gleichen Anteile ergeben
Im vorherigen Aufgabenteil hast du bereits die prozentualen Anteile der einzelnen Altersgruppen für eine konkrete stationäre Verteilung berechnet. Nun sollst du zeigen, dass diese Anteile für jedes  gleich sind. Dazu kannst du genauso vorgehen wie eben, nur dass du nun nicht eine konkrete Verteilung wählst sondern die Verteilung abhängig von
gleich sind. Dazu kannst du genauso vorgehen wie eben, nur dass du nun nicht eine konkrete Verteilung wählst sondern die Verteilung abhängig von  belässt und so in die Formel einsetzt. Anschließend kannst du sehen, ob die prozentualen Anteile noch von
belässt und so in die Formel einsetzt. Anschließend kannst du sehen, ob die prozentualen Anteile noch von  abhängen oder nicht. Ist das der Fall, so ist der Anteil nicht bei jeder stationären Verteilung gleich, ansonsten sind sie für jede Altersgruppe immer gleich. Berechne dazu wieder
abhängen oder nicht. Ist das der Fall, so ist der Anteil nicht bei jeder stationären Verteilung gleich, ansonsten sind sie für jede Altersgruppe immer gleich. Berechne dazu wieder  ,
,  ,
,  und die Gesamtpopulation
und die Gesamtpopulation  , diesmal aber in Abhängigkeit von
, diesmal aber in Abhängigkeit von  .
1. Schritt: Verteilung und Gesamtpopulation berechnen
Für die Verteilung ergibt sich:
.
1. Schritt: Verteilung und Gesamtpopulation berechnen
Für die Verteilung ergibt sich:
 Damit ist:
Damit ist:  ,
,  und
und  .
Für die Gesamtpopulation ergibt sich damit:
.
Für die Gesamtpopulation ergibt sich damit:  .
2. Schritt: Anteile berechnen
Setze nun die Werte aus dem 1. Schritt wieder in die Formel ein, die du zuvor auch verwendet hast:
.
2. Schritt: Anteile berechnen
Setze nun die Werte aus dem 1. Schritt wieder in die Formel ein, die du zuvor auch verwendet hast:


 Die prozentualen Anteile der einzelnen Altersgruppen, sind nicht mehr abhängig von
Die prozentualen Anteile der einzelnen Altersgruppen, sind nicht mehr abhängig von  und daher für jede der angegebenen stationären Verteilungen gleich.
und daher für jede der angegebenen stationären Verteilungen gleich.



- Berechne für ein
, z.B.
, die Verteilung und die Gesamtpopulation
- Berechne den Anteil jeder Altersgruppe an der Gesamtpopulation mit Hilfe der Regeln für die Prozentrechnung
c) (1)  Übergangsmatrix angeben
Hier hast du nun den Übergangsgraphen gegeben, der die Entwicklung einer zweiten Seevogelart beschreibt und sollst ausgehend davon eine zugehörige Übergangsmatrix
Übergangsmatrix angeben
Hier hast du nun den Übergangsgraphen gegeben, der die Entwicklung einer zweiten Seevogelart beschreibt und sollst ausgehend davon eine zugehörige Übergangsmatrix  angeben.
angeben.
Überlege dir zunächst, wie viele Zeilen und spalten die Matrix haben muss. Anschließend kannst du dich um die Einträge von
haben muss. Anschließend kannst du dich um die Einträge von  kümmern.
Im Übergangsgraphen gibt es nur zwei Knoten, also kannst du davon ausgehen, dass es bei dieser Seevogelart nur zwei Altersgruppen gibt. Demnach muss die Übergangsmatrix jeweils zwei Zeilen und Spalten besitzen.
In Aufgabenteil a) (3) hast du gesehen, dass das Element
kümmern.
Im Übergangsgraphen gibt es nur zwei Knoten, also kannst du davon ausgehen, dass es bei dieser Seevogelart nur zwei Altersgruppen gibt. Demnach muss die Übergangsmatrix jeweils zwei Zeilen und Spalten besitzen.
In Aufgabenteil a) (3) hast du gesehen, dass das Element  die Übergangsquote von Altersgruppe
die Übergangsquote von Altersgruppe  in Altersgruppe
in Altersgruppe  beschreibt. In dem Übergangsgraphen findest du diese Quote als Bezeichnung an dem Pfeil vom Knoten
beschreibt. In dem Übergangsgraphen findest du diese Quote als Bezeichnung an dem Pfeil vom Knoten  zum Knoten
zum Knoten  .
Damit ergibt sich dann die folgende Übergangsmatrix:
.
Damit ergibt sich dann die folgende Übergangsmatrix:
 (2)
(2)  Entwicklung der 2. Seevogelart im Vergleich zur 1. beschreiben
Die Beschreibung der Entwicklung der 1. Seevogelart ist dir bereits in der Einführung zur Aufgabe gegeben. Überlege dir hier nun zunächst mit Hilfe des Übergangsgraphen, wie die Entwicklung der 2. Seevogelart abläuft und ziehe anschließend den Vergleich zur 1. Seevogelart.
1. Schritt: Entwicklung der zweiten Seevogelart beschreiben
Betrachte dazu zunächst den allgemeinen Aufbau des Graphen, also die Anzahl der Knoten, die Beschriftung der Knoten usw. Anschließend kannst du die Details betrachten, indem du dir über die Bedeutung der einzelnen Pfeile nacheinander Gedanken machst.
Am Graphen kannst du sehen, dass es bei der zweiten Seevogelart nur zwei Altersgruppen gibt. Da die Übergangsquoten sich wieder auf ein Jahr beziehen, bedeutet dies also, dass diese Seevogelart bereits nach einem Jahr ausgewachsen ist und die erste Brut bereits im zweiten Lebensjahr stattfinden kann.
Daran, dass der Pfeil von (1) nach (2) mit
Entwicklung der 2. Seevogelart im Vergleich zur 1. beschreiben
Die Beschreibung der Entwicklung der 1. Seevogelart ist dir bereits in der Einführung zur Aufgabe gegeben. Überlege dir hier nun zunächst mit Hilfe des Übergangsgraphen, wie die Entwicklung der 2. Seevogelart abläuft und ziehe anschließend den Vergleich zur 1. Seevogelart.
1. Schritt: Entwicklung der zweiten Seevogelart beschreiben
Betrachte dazu zunächst den allgemeinen Aufbau des Graphen, also die Anzahl der Knoten, die Beschriftung der Knoten usw. Anschließend kannst du die Details betrachten, indem du dir über die Bedeutung der einzelnen Pfeile nacheinander Gedanken machst.
Am Graphen kannst du sehen, dass es bei der zweiten Seevogelart nur zwei Altersgruppen gibt. Da die Übergangsquoten sich wieder auf ein Jahr beziehen, bedeutet dies also, dass diese Seevogelart bereits nach einem Jahr ausgewachsen ist und die erste Brut bereits im zweiten Lebensjahr stattfinden kann.
Daran, dass der Pfeil von (1) nach (2) mit  beschriftet ist, kannst du erkennen, dass die Übergangsquote, also sozusagen die Überlebensrate im 1. Lebensjahr,
beschriftet ist, kannst du erkennen, dass die Übergangsquote, also sozusagen die Überlebensrate im 1. Lebensjahr,  beträgt.
Analog dazu bedeutet der Pfeil von (2) zur (1) mit der Beschriftung
beträgt.
Analog dazu bedeutet der Pfeil von (2) zur (1) mit der Beschriftung  , dass ein Vogel im Durchschnitt jedes Jahr
, dass ein Vogel im Durchschnitt jedes Jahr  Nachkommen bekommt.
Der Pfeil von (2) zu (2) mit der Beschriftung
Nachkommen bekommt.
Der Pfeil von (2) zu (2) mit der Beschriftung  ist die Übergangsquote von Altersgruppe 2 nach Altersgruppe 2, also die Überlebensquote eines ausgewachsenen Vogels.
2. Schritt: Vergleich zwischen den beiden Arten
Vergleiche nun schrittweise die Entwicklungen der beiden Arten:
Dabei fällt dir folgendes auf:
ist die Übergangsquote von Altersgruppe 2 nach Altersgruppe 2, also die Überlebensquote eines ausgewachsenen Vogels.
2. Schritt: Vergleich zwischen den beiden Arten
Vergleiche nun schrittweise die Entwicklungen der beiden Arten:
Dabei fällt dir folgendes auf:
Überlege dir zunächst, wie viele Zeilen und spalten die Matrix
- Die 1. Seevogelart wird in drei Altersgruppen eingeteilt und ist erst nach zwei Jahren ausgewachsen und brutfähig, die 2. Seevogelart ist dagegen in nur zwei Altersgruppen eingeteilt worden und bereits nach dem ersten Lebensjahr ausgewachsen und brutfähig.
- Bei den Jungvögeln der 1. Seevogelart beträgt die Überlebensquote
, bei der 2. Art überleben weniger Jungtiere, hier beträgt die Überlebensquote
.
- Bei den Altvögeln, ist die Überlebensquote der 2. Seevogelart ebenfalls niedriger, diese beträgt
und die der 1. Art
.
- Der Bruterfolg ist allerdings bei der 2. Art höher: Hier bekommt jeder Altvogel durchschnittlich
Nachkommen pro Jahr, bei der 2. Art sind es
bzw. nach der Einführung der Schutzmaßnahmen
Nachkommen pro Vogel und pro Jahr.
a) (1)  Verteilung der Vögel nach einem und zwei Jahren berechnen
Deine Aufgabe ist es hier, die Verteilung der Vögel nach einem und nach zwei Jahren zu berechnen, wobei dir die aktuelle Verteilung gegeben ist mit:
Verteilung der Vögel nach einem und zwei Jahren berechnen
Deine Aufgabe ist es hier, die Verteilung der Vögel nach einem und nach zwei Jahren zu berechnen, wobei dir die aktuelle Verteilung gegeben ist mit:
 Die Übergangsmatrix ist dir ebenfalls gegeben mit
Die Übergangsmatrix ist dir ebenfalls gegeben mit  Hierbei bietet sich die folgende Formel an, um die Verteilung zum Zeitpunkt
Hierbei bietet sich die folgende Formel an, um die Verteilung zum Zeitpunkt  zu berechnen:
zu berechnen:
 Dort kannst du nun
Dort kannst du nun  ,
,  für
für  und
und  bzw
bzw  einsetzen und erhältst so die Verteilung der Vögel nach ein bzw. zwei Jahren.
Dabei kannst du deinen GTR zu Hilfe nehmen oder auch handschriftlich rechnen.
einsetzen und erhältst so die Verteilung der Vögel nach ein bzw. zwei Jahren.
Dabei kannst du deinen GTR zu Hilfe nehmen oder auch handschriftlich rechnen.
 Lösungsweg A: Handschriftlich
Hierbei kannst du zunächst die Verteilung nach einem Jahr berechnen und diese zur Berechnung der Verteilung im zweiten Jahr wieder verwenden:
Lösungsweg A: Handschriftlich
Hierbei kannst du zunächst die Verteilung nach einem Jahr berechnen und diese zur Berechnung der Verteilung im zweiten Jahr wieder verwenden:
 Nach einem Jahr sind
Nach einem Jahr sind  Jungvögel,
Jungvögel,  Vögel im 2. Lebensjahr und
Vögel im 2. Lebensjahr und  Altvögel vorhanden.
Nun kennst du
Altvögel vorhanden.
Nun kennst du  und kannst damit
und kannst damit  berechnen:
berechnen:
 Nach zwei Jahren sind
Nach zwei Jahren sind  Jungvögel,
Jungvögel,  Vögel im zweiten Lebensjahr und
Vögel im zweiten Lebensjahr und  Altvögel vorhanden.
Altvögel vorhanden.
 Lösungsweg B: GTR
Mit dem GTR kannst du hier am besten arbeiten, indem du zunächst die Übergangsmatrix
Lösungsweg B: GTR
Mit dem GTR kannst du hier am besten arbeiten, indem du zunächst die Übergangsmatrix  unter der Bezeichnung
unter der Bezeichnung  speicherst. Dies kannst du im CALC-menü tun. Wähle dazu unter
speicherst. Dies kannst du im CALC-menü tun. Wähle dazu unter
 aus. Anschließend musst du zunächst die Dimension der Matrix (3 x 3) und anschließend die Matrixeinträge eingeben. Verlasse das Matrixmenü anschließend wieder. Das gleiche kannst du mit dem Verteilungsvektor
aus. Anschließend musst du zunächst die Dimension der Matrix (3 x 3) und anschließend die Matrixeinträge eingeben. Verlasse das Matrixmenü anschließend wieder. Das gleiche kannst du mit dem Verteilungsvektor  tun und ihn unter
tun und ihn unter  abspeichern. Dieser hat die Dimension 3 x 1.
abspeichern. Dieser hat die Dimension 3 x 1.
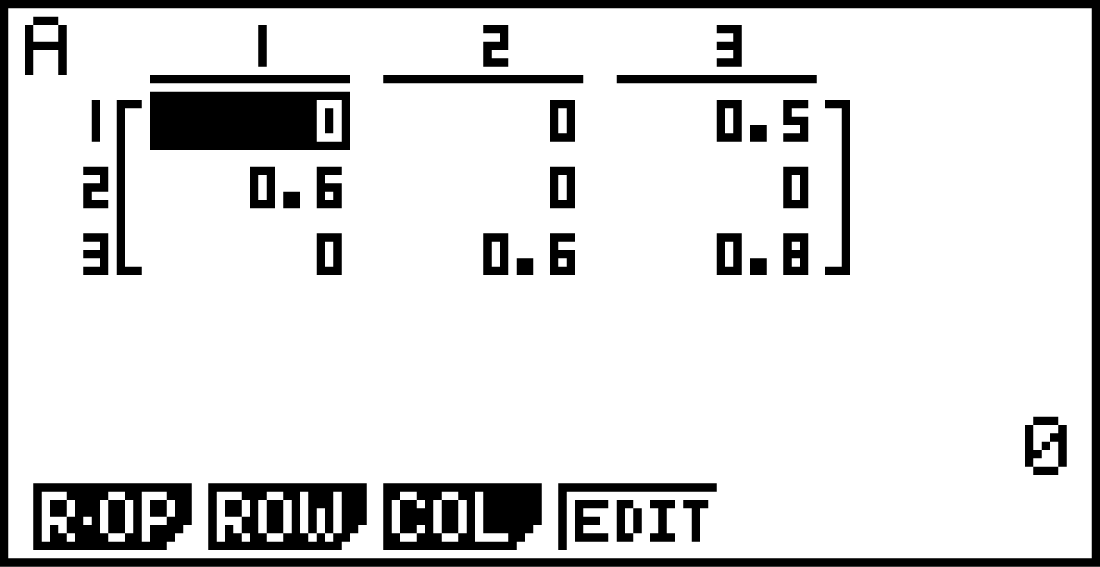
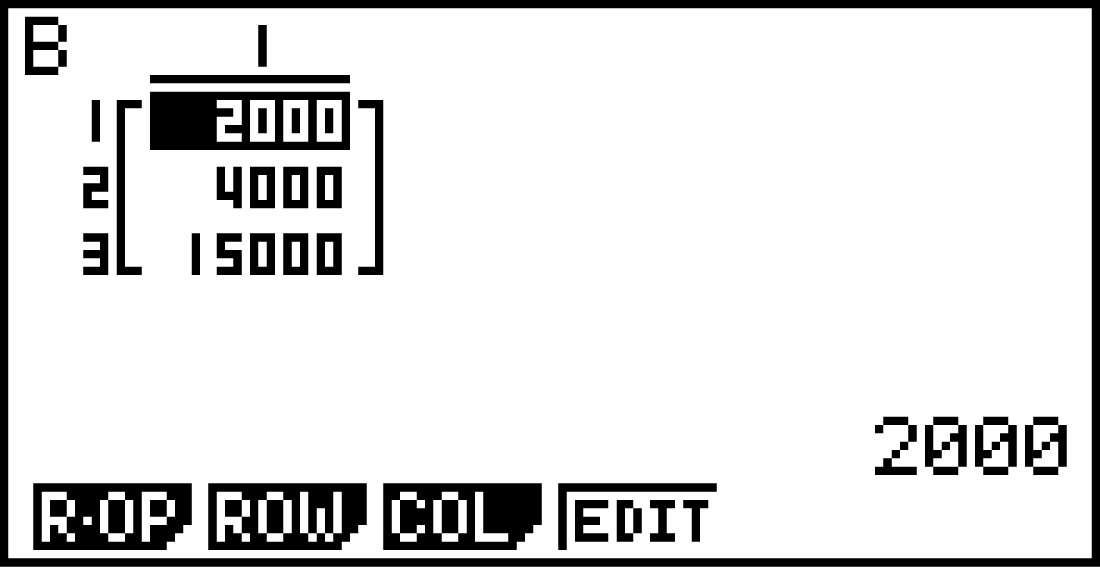 Dann kannst du anschließend
Dann kannst du anschließend  berechnen, indem du die Matrix bzw. den Vektor wieder aufrufst. Den Befehl um eine Matrix abzurufen findest du unter:
berechnen, indem du die Matrix bzw. den Vektor wieder aufrufst. Den Befehl um eine Matrix abzurufen findest du unter:

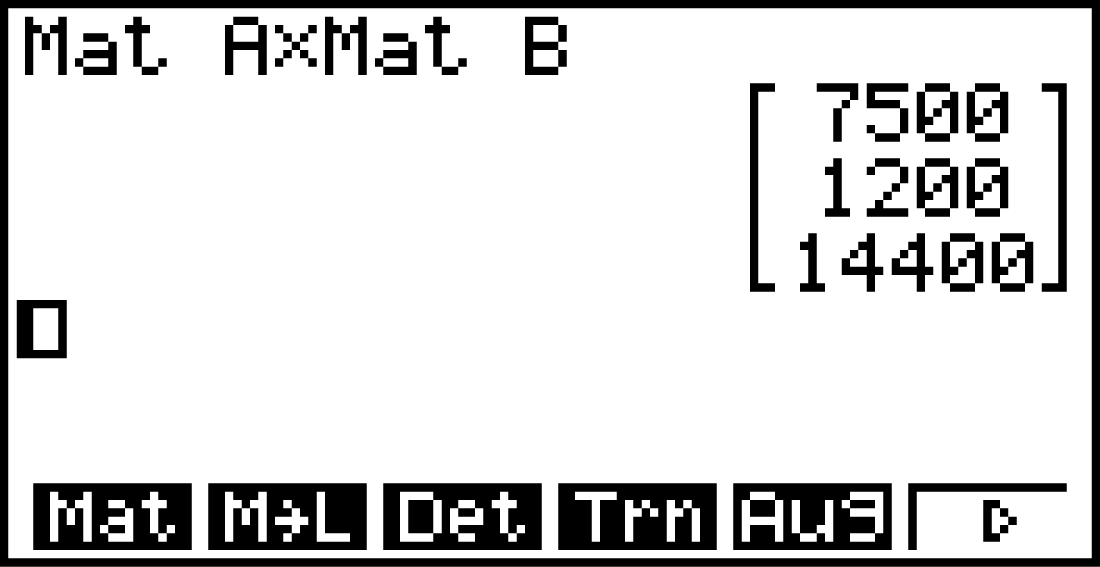 Nach einem Jahr sind
Nach einem Jahr sind  Jungvögel,
Jungvögel,  Vögel im 2. Lebensjahr und
Vögel im 2. Lebensjahr und  Altvögel vorhanden.
Genauso kannst du nun auch die Verteilung nach zwei Jahren berechnen, indem du den Verteilungsvektor
Altvögel vorhanden.
Genauso kannst du nun auch die Verteilung nach zwei Jahren berechnen, indem du den Verteilungsvektor  als C speicherst:
als C speicherst:

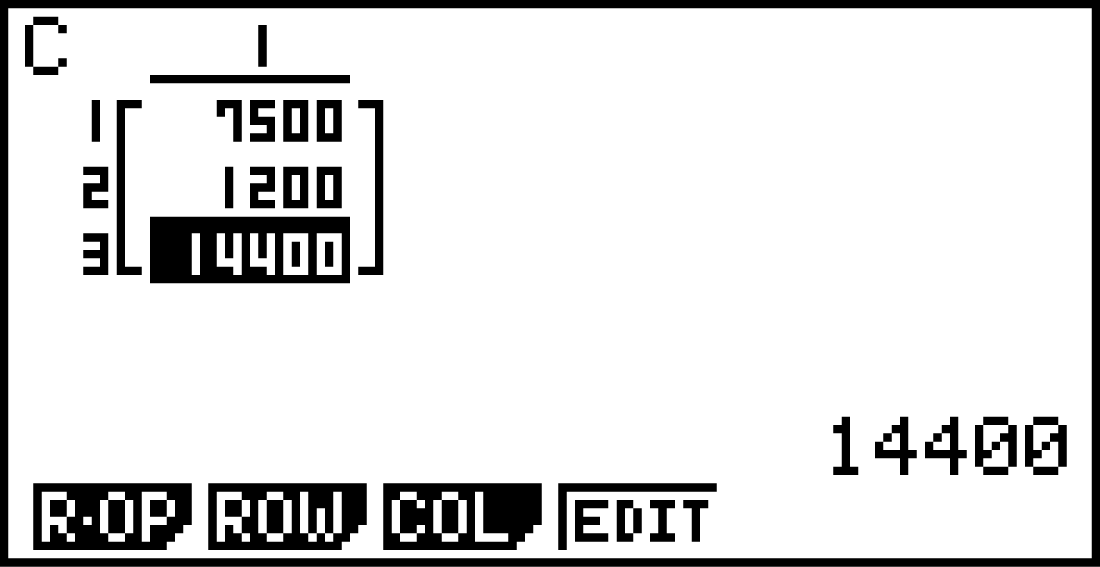
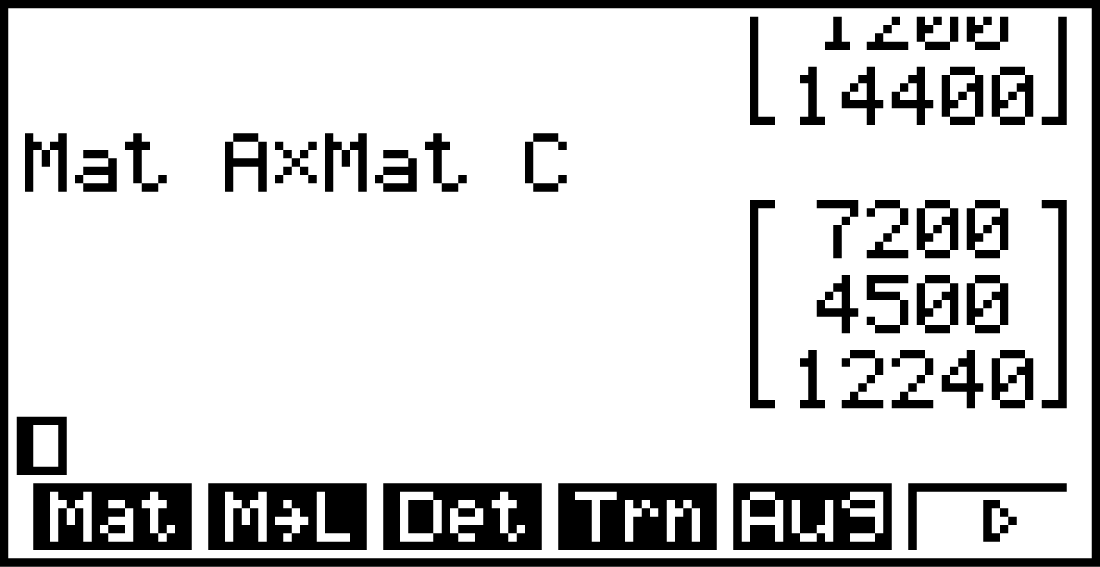 Nach zwei Jahren sind
Nach zwei Jahren sind  Jungvögel,
Jungvögel,  Vögel im zweiten Lebensjahr und
Vögel im zweiten Lebensjahr und  Altvögel vorhanden.
(2)
Altvögel vorhanden.
(2)  Verteilung für das Vorjahr berechnen
Nun sollst du die Verteilung für das Vorjahr berechnen. Also die Anzahl der verschiedenen Altersgruppen der Vögel zum Zeitpunkt
Verteilung für das Vorjahr berechnen
Nun sollst du die Verteilung für das Vorjahr berechnen. Also die Anzahl der verschiedenen Altersgruppen der Vögel zum Zeitpunkt  . Hier kannst du wieder die Formel von oben anwenden, und zwar kennst du in diesem Fall den Verteilungsvektor
. Hier kannst du wieder die Formel von oben anwenden, und zwar kennst du in diesem Fall den Verteilungsvektor  und die Übergangsmatrix
und die Übergangsmatrix  und du suchst den Verteilungsvektor
und du suchst den Verteilungsvektor
 ,
das heißt die Verteilung, sodass daraus ein Jahr später die Verteilung
,
das heißt die Verteilung, sodass daraus ein Jahr später die Verteilung  entsteht.
Insgesamt suchst du also den Verteilungsvektor
entsteht.
Insgesamt suchst du also den Verteilungsvektor  , der die folgende Gleichung erfüllt:
, der die folgende Gleichung erfüllt:
 Setzt du dort die Informationen ein, so kannst du aus dieser Gleichung ein
lineares Gleichungssystem in Abhängigkeit von
Setzt du dort die Informationen ein, so kannst du aus dieser Gleichung ein
lineares Gleichungssystem in Abhängigkeit von  ,
,  und
und  gewinnen, welches du anschließend entweder mit dem GTR oder per Hand lösen kannst.
1. Schritt: Lineares Gleichungssystem aufstellen
Setzt du
gewinnen, welches du anschließend entweder mit dem GTR oder per Hand lösen kannst.
1. Schritt: Lineares Gleichungssystem aufstellen
Setzt du  und
und  in die Gleichung ein, so erhältst du folgende Gleichung:
in die Gleichung ein, so erhältst du folgende Gleichung:
 Dort kannst du nun jede „Zeile“ einzeln ablesen. Dann erhältst du das folgende lineare Gleichungssystem:
Dort kannst du nun jede „Zeile“ einzeln ablesen. Dann erhältst du das folgende lineare Gleichungssystem:
 2. Schritt: Gleichungssystem lösen
Hier hast du auch wieder zwei Möglichkeiten, entweder du löst das LGS mit Hilfe des GTR oder handschriftlich.
2. Schritt: Gleichungssystem lösen
Hier hast du auch wieder zwei Möglichkeiten, entweder du löst das LGS mit Hilfe des GTR oder handschriftlich.
 Lösungsweg A: Handschriftlich
Du kannst schnell erkennen, dass die erste und zweite Gleichung des LGS jeweils von nur einer Variablen abhängen. Außerdem weißt du, dass du aus einer Gleichung mit einer Variablen die Lösung für die Variablen direkt bestimmen kannst.
Du kannst hier also wie folgt vorgehen:
Lösungsweg A: Handschriftlich
Du kannst schnell erkennen, dass die erste und zweite Gleichung des LGS jeweils von nur einer Variablen abhängen. Außerdem weißt du, dass du aus einer Gleichung mit einer Variablen die Lösung für die Variablen direkt bestimmen kannst.
Du kannst hier also wie folgt vorgehen:
 Aus der zweiten Gleichung erhältst du:
Aus der zweiten Gleichung erhältst du:
 Setzt du dies nun in (3) ein, so kannst du nach
Setzt du dies nun in (3) ein, so kannst du nach  auflösen:
auflösen:
 Aus dem Modell ergäbe sich die folgende Verteilung für das Vorjahr:
Es waren ca. 6.667 Jungvögel, 19.667 Vögel im 2. Lebensjahr und 4.000 Altvögel vorhanden.
Aus dem Modell ergäbe sich die folgende Verteilung für das Vorjahr:
Es waren ca. 6.667 Jungvögel, 19.667 Vögel im 2. Lebensjahr und 4.000 Altvögel vorhanden.
 Lösungsweg B: GTR
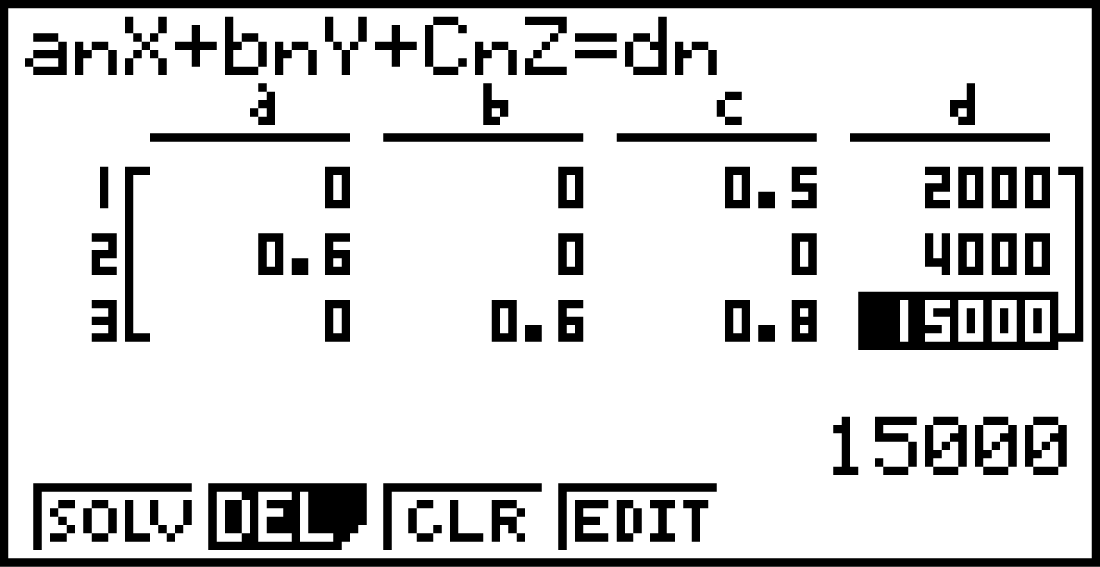
Mit dem GTR kannst du das LGS im EQUA-Menü lösen. Wähle dort mit F1 den Menüpunkt Lin Gleichungssyst und gib die Anzahl der Unbekannten (3) an.
Anschließend kannst du die Koeffizienten des LGS eingeben und mit EXE bestätigen.
Lösungsweg B: GTR
Mit dem GTR kannst du das LGS im EQUA-Menü lösen. Wähle dort mit F1 den Menüpunkt Lin Gleichungssyst und gib die Anzahl der Unbekannten (3) an.
Anschließend kannst du die Koeffizienten des LGS eingeben und mit EXE bestätigen.
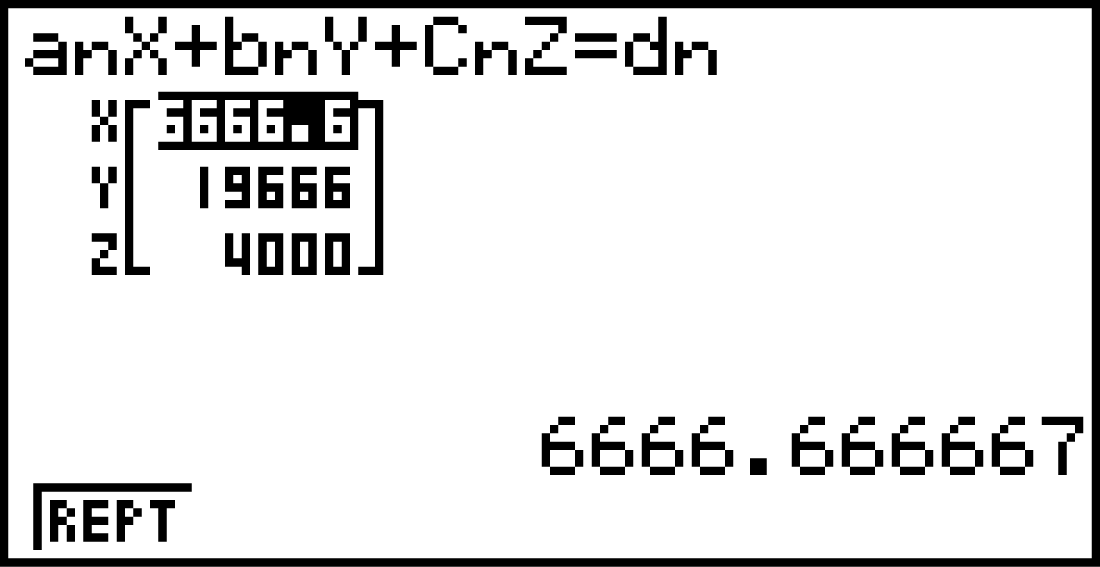 Dann erhältst du das Ergebnis:
Dann erhältst du das Ergebnis:
 ,
,  ,
,  Aus dem Modell ergäbe sich die folgende Verteilung für das Vorjahr:
Es waren ca. 6.667 Jungvögel, 19.667 Vögel im 2. Lebensjahr und 4.000 Altvögel vorhanden.
(3)
Aus dem Modell ergäbe sich die folgende Verteilung für das Vorjahr:
Es waren ca. 6.667 Jungvögel, 19.667 Vögel im 2. Lebensjahr und 4.000 Altvögel vorhanden.
(3)  Nullwerte der Matrix erklären
In diesem Aufgabenteil, sollst du für jedes Element der Matrix
Nullwerte der Matrix erklären
In diesem Aufgabenteil, sollst du für jedes Element der Matrix  , das den Wert Null hat, erklären, warum es eben diesen Wert hat. Am besten kannst du dabei schrittweise für jedes Element einzeln vorgehen.
Die folgenden Elemente der Matrix
, das den Wert Null hat, erklären, warum es eben diesen Wert hat. Am besten kannst du dabei schrittweise für jedes Element einzeln vorgehen.
Die folgenden Elemente der Matrix  haben den Wert Null:
haben den Wert Null:
 gibt dabei den Anteil der Vögel an, die im nächsten Jahr von Altersgruppe
gibt dabei den Anteil der Vögel an, die im nächsten Jahr von Altersgruppe  in Altersgruppe
in Altersgruppe  übergehen. Bei den Altvögeln bedeutet
übergehen. Bei den Altvögeln bedeutet  beispielsweise, dass jeder Altvogel im Schnitt pro Jahr
beispielsweise, dass jeder Altvogel im Schnitt pro Jahr  Nachkommen hat.
Erklärung für
Nachkommen hat.
Erklärung für  Das erste Element
Das erste Element  beschreibt den Anteil der Vögel, die nach einem Jahr vom Stadium
beschreibt den Anteil der Vögel, die nach einem Jahr vom Stadium  immer noch im Stadium
immer noch im Stadium  bleiben. Da
bleiben. Da  aber das Stadium der Vögel im ersten Lebensjahr bezeichnet, ist dieser Wert Null, weil ein Vogel nicht zwei Jahre hintereinander im 1. Lebensjahr sein kann.
Erklärung für
aber das Stadium der Vögel im ersten Lebensjahr bezeichnet, ist dieser Wert Null, weil ein Vogel nicht zwei Jahre hintereinander im 1. Lebensjahr sein kann.
Erklärung für 
 beschreibt den Anteil der Vögel, die von der Altersgruppe
beschreibt den Anteil der Vögel, die von der Altersgruppe  in die Altersgruppe
in die Altersgruppe  übergehen. Für einen solchen Übergang müsste folgendes passieren:
übergehen. Für einen solchen Übergang müsste folgendes passieren:

 hat aus ähnlichen Gründen den Wert Null, wie
hat aus ähnlichen Gründen den Wert Null, wie  . Nach einem Jahr ist jeder Vogel entweder ein Jahr älter oder gestorben. Ist er vorher in Altersgruppe
. Nach einem Jahr ist jeder Vogel entweder ein Jahr älter oder gestorben. Ist er vorher in Altersgruppe  , also im zweiten Lebensjahr, so kann er im nächsten Jahr nicht noch einmal in Altergruppe
, also im zweiten Lebensjahr, so kann er im nächsten Jahr nicht noch einmal in Altergruppe  sein. Daher hat
sein. Daher hat  den Wert Null.
Erklärung für
den Wert Null.
Erklärung für  Hierbei verläuft die Erklärung analog zu
Hierbei verläuft die Erklärung analog zu  .
.  beschreibt den Anteil der Vögel, die von Altersgruppe
beschreibt den Anteil der Vögel, die von Altersgruppe  nach einem Jahr zurück in Altersgruppe
nach einem Jahr zurück in Altersgruppe  übergeht. Dies würde aber bedeuten, dass ein Vogel vom dritten Lebensjahr, ein Jahr später im 2. Lebensjahr wäre. Dies ist unmöglich. Nachkommen, die nach einem Jahr bereits das zweite Lebensjahr erreicht haben, kann ein Altvogel auch nicht produzieren. Daher hat
übergeht. Dies würde aber bedeuten, dass ein Vogel vom dritten Lebensjahr, ein Jahr später im 2. Lebensjahr wäre. Dies ist unmöglich. Nachkommen, die nach einem Jahr bereits das zweite Lebensjahr erreicht haben, kann ein Altvogel auch nicht produzieren. Daher hat  den Wert Null.
Erklärung für
den Wert Null.
Erklärung für 
 beschreibt den Anteil der Vögel aus Altersgruppe
beschreibt den Anteil der Vögel aus Altersgruppe  , die nach einem Jahr Altersgruppe
, die nach einem Jahr Altersgruppe  angehören. Da dies aber bedeuten würde, dass ein Vogel das zweite Lebensjahr überspringen würde, ist dies unmöglich. Daher ist
angehören. Da dies aber bedeuten würde, dass ein Vogel das zweite Lebensjahr überspringen würde, ist dies unmöglich. Daher ist  .
.
F3: MAT
die Bezeichnung 

OPTN  F2: MAT
F2: MAT  F1: MAT
F1: MAT
Setze dahinter die Bezeichnung der gewünschten Matrix.



- Löse (1) nach
und bestimme so die Lösung für
- Löse (2) nach
und bestimme so die Lösung für
- Setze die Lösungen aus den ersten beiden Schritten in (3) ein und bestimme die Lösung für
durch Umformen von (3)

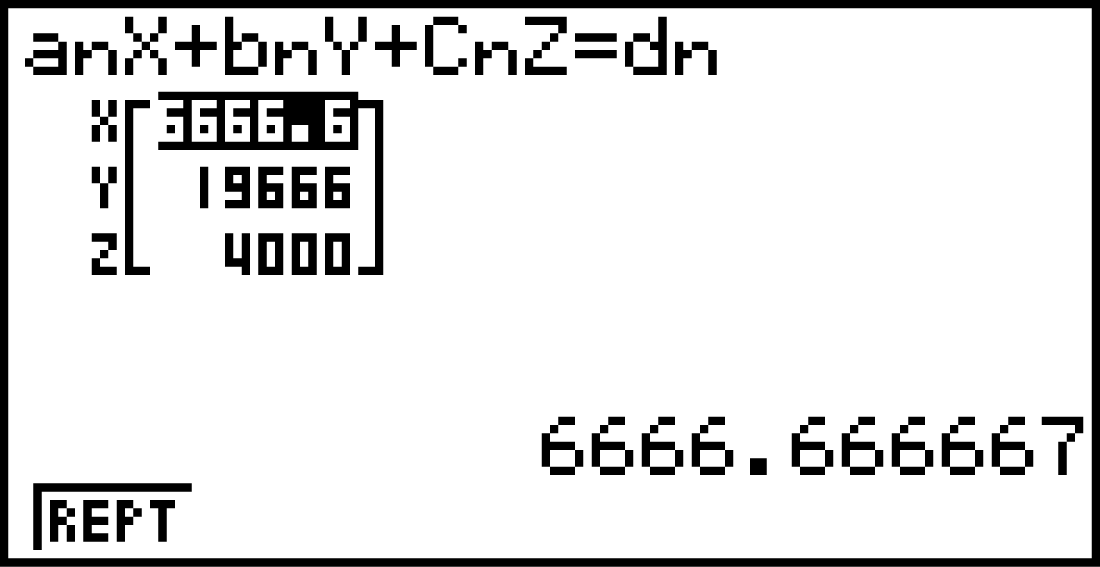
- Ein Vogel, der im zweiten Lebensjahr ist, ist ein Jahr später wieder im ersten Lebensjahr oder
- Ein Vogel im zweiten Lebensjahr zeugt Nachkommen
b) (1)  Auf stationäre Verteilungen untersuchen
Hier ist es deine Aufgabe, zu untersuchen, ob es eine von
Auf stationäre Verteilungen untersuchen
Hier ist es deine Aufgabe, zu untersuchen, ob es eine von  verschiedene stationäre Verteilung gibt. Eine stationäre Verteilung ist eine Verteilung
verschiedene stationäre Verteilung gibt. Eine stationäre Verteilung ist eine Verteilung  , sodass
, sodass  usw. gilt. Das bedeutet,
usw. gilt. Das bedeutet,  muss die folgende Gleichung erfüllen:
muss die folgende Gleichung erfüllen:
 Aus dieser Gleichung ergibt sich mit
Aus dieser Gleichung ergibt sich mit  wieder ein lineares Gleichungssystem in Abhängigkeit von
wieder ein lineares Gleichungssystem in Abhängigkeit von  ,
,  und
und  . Dieses kannst du dann wieder mit dem GTR oder auch handschriftlich lösen.
1. Schritt: Lineares Gleichungssystem aufstellen
Das lineare Gleichungssystem kannst du wieder wie in Aufgabenteil a) (2) aufstellen, indem du die Matrix und den Vektor miteinander multiplizierst und anschließend jede „Zeile“ einzeln abliest:
. Dieses kannst du dann wieder mit dem GTR oder auch handschriftlich lösen.
1. Schritt: Lineares Gleichungssystem aufstellen
Das lineare Gleichungssystem kannst du wieder wie in Aufgabenteil a) (2) aufstellen, indem du die Matrix und den Vektor miteinander multiplizierst und anschließend jede „Zeile“ einzeln abliest:
 Daraus ergibt sich dann das folgende LGS:
Daraus ergibt sich dann das folgende LGS:
 2. Schritt: Gleichungssystem lösen
Das LGS kannst du nun handschriftlich oder mit dem GTR lösen.
2. Schritt: Gleichungssystem lösen
Das LGS kannst du nun handschriftlich oder mit dem GTR lösen.
 Lösungsweg A: Handschriftlich
Hier kannst du mit dem Einsetzungsverfahren arbeiten. Wie du siehst, hast du
Lösungsweg A: Handschriftlich
Hier kannst du mit dem Einsetzungsverfahren arbeiten. Wie du siehst, hast du  in Abhängigkeit von
in Abhängigkeit von  dargestellt und
dargestellt und  in Abhängigkeit von
in Abhängigkeit von  . Setzt du nun
. Setzt du nun  in (2) ein, so erhältst du
in (2) ein, so erhältst du  ebenfalls in Abhängigkeit von
ebenfalls in Abhängigkeit von  . Dann kannst du diese Darstellungsweisen von
. Dann kannst du diese Darstellungsweisen von  und
und  in (3) einsetzen, die dann nur noch von
in (3) einsetzen, die dann nur noch von  abhängt. So kannst du eine Lösung für
abhängt. So kannst du eine Lösung für  bestimmen und anschließend die Lösungen für
bestimmen und anschließend die Lösungen für  und
und  .
.
 Setzt du nun
Setzt du nun  und
und  in (3) ein, so erhältst du:
in (3) ein, so erhältst du:
 Mit
Mit  ergibt sich für
ergibt sich für  und
und  :
:

 Damit wäre also
Damit wäre also  , was der Voraussetzung widerspricht.
Es existiert keine stationäre Verteilung außer
, was der Voraussetzung widerspricht.
Es existiert keine stationäre Verteilung außer  .
.
 Lösungsweg B: GTR
Um das LGS wie zuvor mit dem GTR zu lösen, musst du zunächst alle
Lösungsweg B: GTR
Um das LGS wie zuvor mit dem GTR zu lösen, musst du zunächst alle  auf eine Seite bringen. Dann wird aus
auf eine Seite bringen. Dann wird aus

 Nun kannst du das LGS wie in Aufgabenteil a) mit dem Menüpunkt Lineares Gleichungssystem im EQUA-Menü deines GTR lösen und erhältst:
Nun kannst du das LGS wie in Aufgabenteil a) mit dem Menüpunkt Lineares Gleichungssystem im EQUA-Menü deines GTR lösen und erhältst:

 Damit existiert keine stationäre Verteilung außer
Damit existiert keine stationäre Verteilung außer  .
(2)
.
(2)  Prozentsatz berechnen
Nun sollst du den Prozentsatz
Prozentsatz berechnen
Nun sollst du den Prozentsatz  näherungsweise berechnen, um den sich die Gesamtpopulation der Vögel jährlich verkleinert. Du hast dazu die Gesamtpopulation
näherungsweise berechnen, um den sich die Gesamtpopulation der Vögel jährlich verkleinert. Du hast dazu die Gesamtpopulation  zu zwei Zeitpunkten
zu zwei Zeitpunkten  und
und  gegeben:
gegeben:

 Wenn sich die Gesamtpopulation
Wenn sich die Gesamtpopulation  innerhalb eines Jahres um den Prozentsatz
innerhalb eines Jahres um den Prozentsatz  verkleinert, so bleibt ein Anteil von
verkleinert, so bleibt ein Anteil von  der Population erhalten. Also gilt aufgrund der Regeln der Prozentrechnung:
der Population erhalten. Also gilt aufgrund der Regeln der Prozentrechnung:
 Du kennst nun aber nicht zwei Werte, die nur ein Jahr auseinander liegen, sondern zwei Werte, die 10 Jahre auseinander liegen. Du suchst also eine Formel für
Du kennst nun aber nicht zwei Werte, die nur ein Jahr auseinander liegen, sondern zwei Werte, die 10 Jahre auseinander liegen. Du suchst also eine Formel für  in Abhängigkeit von
in Abhängigkeit von  . Aus der obigen Formel kannst du solch eine Formel herleiten und anschließend mit Hilfe der gegebenen Werte eine Gleichung in Abhängigkeit von
. Aus der obigen Formel kannst du solch eine Formel herleiten und anschließend mit Hilfe der gegebenen Werte eine Gleichung in Abhängigkeit von  aufstellen und so anschließend
aufstellen und so anschließend  berechnen.
1. Schritt: Gleichung aufstellen
Du weißt, dass
berechnen.
1. Schritt: Gleichung aufstellen
Du weißt, dass  gilt. Das gleiche kannst du auch für
gilt. Das gleiche kannst du auch für  formulieren:
formulieren:
 Dort kannst du nun wieder die Formel für
Dort kannst du nun wieder die Formel für  einsetzen und erhältst:
einsetzen und erhältst:
 Du kannst folgendes erkennen: Setzt du dies immer weiter fort, bis du
Du kannst folgendes erkennen: Setzt du dies immer weiter fort, bis du  erhältst so kommt jedes mal einmal der Faktor
erhältst so kommt jedes mal einmal der Faktor  hinzu:
hinzu:
 2. Schritt: Gleichung aufstellen und lösen
Setzt du nun die beiden Werte in die Formel ein, so erhältst du die folgende Gleichung:
2. Schritt: Gleichung aufstellen und lösen
Setzt du nun die beiden Werte in die Formel ein, so erhältst du die folgende Gleichung:
 Diese Gleichung kannst du nun entweder handschriftlich oder auch mit Hilfe des GTR lösen.
Diese Gleichung kannst du nun entweder handschriftlich oder auch mit Hilfe des GTR lösen.
 Lösungsweg A: Handschriftlich
Lösungsweg A: Handschriftlich
![\(\begin{array}{rll}
15.422 &=&(1-p)^{10} \cdot 17.870&\scriptsize{ \mid\; : 17.870 }\\
0,86301&\approx&(1-p)^{10}&\scriptsize{ \mid\; \sqrt[10]{\quad}}\\
0,98538&\approx&1-p&\scriptsize{ \mid\; -1}\\
-0,01462&\approx&-p&\scriptsize{ \mid\; \cdot (-1)}\\
0,01462&\approx&p\\
1,462\,\%&\approx&p\\
\end{array}\)](https://mathjax.schullv.de/c2640585ef082f79c28385a8d573eaa748ed90db3171300cbc7bd9b70bc8896d?color=5a5a5a) Die Gesamtpopulation der Seevögel reduziert sich jährlich um einen Prozentsatz von
Die Gesamtpopulation der Seevögel reduziert sich jährlich um einen Prozentsatz von  .
.
 Lösungsweg B: GTR
Mit dem GTR kannst du die Gleichung im Graph-Menü lösen, indem du den rechten Teil als Funktionsterm einer Funktion
Lösungsweg B: GTR
Mit dem GTR kannst du die Gleichung im Graph-Menü lösen, indem du den rechten Teil als Funktionsterm einer Funktion  in Abhängigkeit von
in Abhängigkeit von  auffasst. Nun suchst du den Wert für
auffasst. Nun suchst du den Wert für  , sodass
, sodass  . Lässt du dir den Graphen von
. Lässt du dir den Graphen von  anzeigen, so kannst du den gesuchten Wert von
anzeigen, so kannst du den gesuchten Wert von  unter
unter
 eingibst. Bestätigst du anschließend mit EXE, so erhältst du die Lösung:
eingibst. Bestätigst du anschließend mit EXE, so erhältst du die Lösung:  .
.
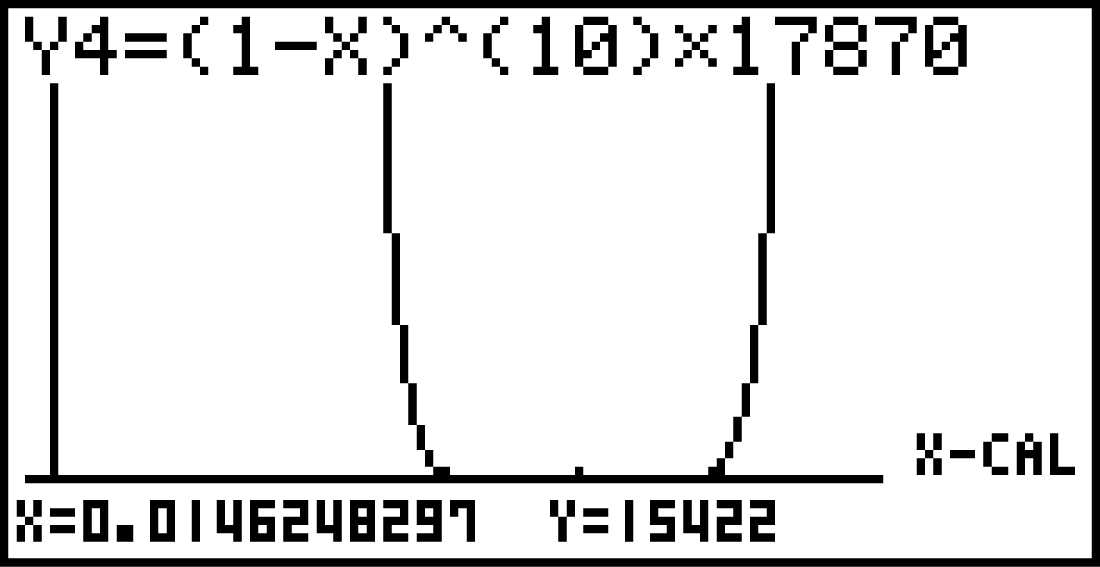 Die Gesamtpopulation der Seevögel reduziert sich jährlich um einen Prozentsatz von
Die Gesamtpopulation der Seevögel reduziert sich jährlich um einen Prozentsatz von  .
(3)
.
(3)  Anzahl der Jahre ermitteln, in denen sich die Population halbiert
In dieser Aufgabe sollst du nun die Anzahl der Jahre ermitteln, nach denen sich die Population halbiert. Das heißt, du sollst
Anzahl der Jahre ermitteln, in denen sich die Population halbiert
In dieser Aufgabe sollst du nun die Anzahl der Jahre ermitteln, nach denen sich die Population halbiert. Das heißt, du sollst  finden, sodass die folgende Gleichung gilt:
finden, sodass die folgende Gleichung gilt:
 Aus dem vorherigen Aufgabenteil weißt du, dass du
Aus dem vorherigen Aufgabenteil weißt du, dass du  auf folgende Weise berechnen kannst:
auf folgende Weise berechnen kannst:
 }
Da du
}
Da du  kennst, kannst du dies in die obere Gleichung einsetzen und erhältst so eine Gleichung in Abhängigkeit von
kennst, kannst du dies in die obere Gleichung einsetzen und erhältst so eine Gleichung in Abhängigkeit von  . Diese kannst du dann nach
. Diese kannst du dann nach  lösen.
lösen.
 Diese Gleichung kannst du nun ebenfalls wieder handschriftlich oder mit dem GTR lösen.
Diese Gleichung kannst du nun ebenfalls wieder handschriftlich oder mit dem GTR lösen.
 Lösungsweg A: Handschriftlich
Handschriftlich kannst du die Gleichung nun weiter nach
Lösungsweg A: Handschriftlich
Handschriftlich kannst du die Gleichung nun weiter nach  umformen, indem du einen Logarithmus anwendest, beispielsweise den Logarithmus zur Basis
umformen, indem du einen Logarithmus anwendest, beispielsweise den Logarithmus zur Basis  . Dann erhältst du:
. Dann erhältst du:
 Nach etwa
Nach etwa  Jahren halbiert sich die Population jeweils.
Jahren halbiert sich die Population jeweils.
 Lösungsweg B: GTR
Um die Gleichung mit Hilfe des GTR zu lösen, kannst du den linken Teil der Gleichung wieder als Funtionsterm auffassen. Dann kannst du im Graph-Menü wie eben den gesuchten Wert für
Lösungsweg B: GTR
Um die Gleichung mit Hilfe des GTR zu lösen, kannst du den linken Teil der Gleichung wieder als Funtionsterm auffassen. Dann kannst du im Graph-Menü wie eben den gesuchten Wert für  berechnen und erhältst:
berechnen und erhältst:

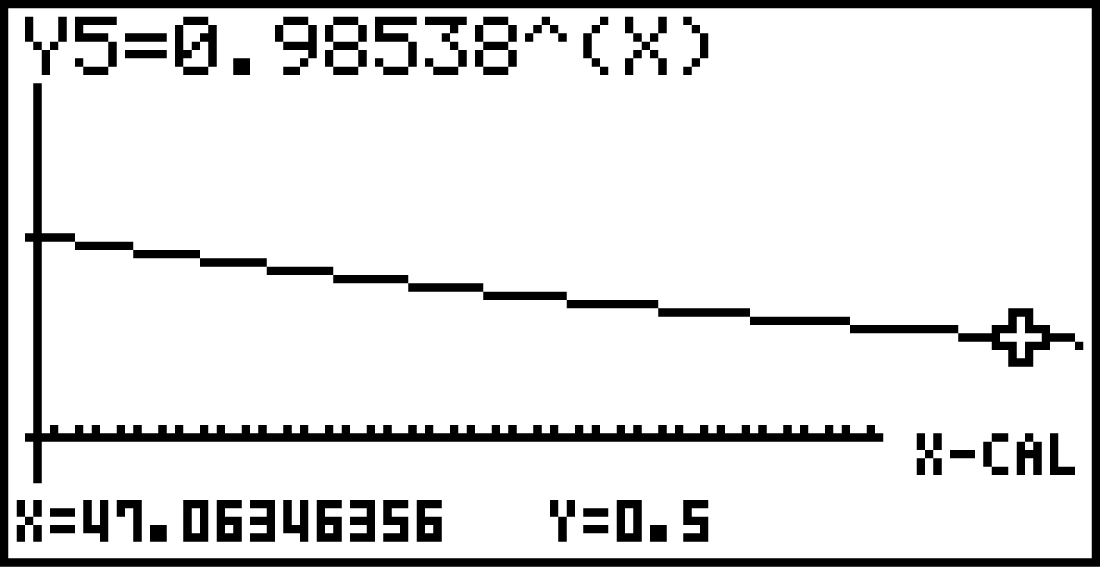 Nach etwa
Nach etwa  Jahren halbiert sich die Population jeweils.
(4)
Jahren halbiert sich die Population jeweils.
(4)  Zeigen, dass die angegebene Verteilung stationär ist
Du sollst zeigen, dass die Verteilung
Zeigen, dass die angegebene Verteilung stationär ist
Du sollst zeigen, dass die Verteilung  für jede positive ganze Zahl
für jede positive ganze Zahl  eine stationäre Verteilung ist. Was eine stationäre Verteilung ist, weißt du bereits aus Aufgabenteil b) (1). Da sich nun aber der Bruterfolg der Seevögel durch Schutzmaßnahmen verbessert hat, musst du hier die Matrix zunächst anpassen. Wie du weißt, beschreibt der Eintrag
eine stationäre Verteilung ist. Was eine stationäre Verteilung ist, weißt du bereits aus Aufgabenteil b) (1). Da sich nun aber der Bruterfolg der Seevögel durch Schutzmaßnahmen verbessert hat, musst du hier die Matrix zunächst anpassen. Wie du weißt, beschreibt der Eintrag  die Anzahl der Nachkommen pro Jahr pro Altvogel. Dies ist also der Eintrag, den du ersetzen musst. Damit ergibt sich die „neue“ Matrix mit:
die Anzahl der Nachkommen pro Jahr pro Altvogel. Dies ist also der Eintrag, den du ersetzen musst. Damit ergibt sich die „neue“ Matrix mit:
 Um nun zu zeigen, dass
Um nun zu zeigen, dass  eine stationäre Verteilung ist, kannst du die Gleichung aus Aufgabenteil b) (1) anwenden. Damit
eine stationäre Verteilung ist, kannst du die Gleichung aus Aufgabenteil b) (1) anwenden. Damit  eine stationäre Verteilung zu der neuen Übergangsmatrix ist, muss gelten:
eine stationäre Verteilung zu der neuen Übergangsmatrix ist, muss gelten:
 Setzt du dort die Matrix und die Verteilung ein, so kannst du nachrechnen, ob diese Gleichung stimmt:
Setzt du dort die Matrix und die Verteilung ein, so kannst du nachrechnen, ob diese Gleichung stimmt:
 Diese Gleichung stimmt, und damit ist
Diese Gleichung stimmt, und damit ist  eine stationäre Verteilung für alle positiven ganzen Zahlen
eine stationäre Verteilung für alle positiven ganzen Zahlen  .
(5)
.
(5)  Prozentuale Anteile berechnen
Hier ist es deine Aufgabe, für eine der stationären Verteilung aus (4) die prozentualen Anteile der einzelnen Altersgruppen an der Gesamtpopulation zu berechnen. Das bedeutet, du sollst nun für ein
Prozentuale Anteile berechnen
Hier ist es deine Aufgabe, für eine der stationären Verteilung aus (4) die prozentualen Anteile der einzelnen Altersgruppen an der Gesamtpopulation zu berechnen. Das bedeutet, du sollst nun für ein  deiner Wahl berechnen, wie viel Prozent der Vögel Jungvögel, Vögel im 2. Lebensjahr oder Altvögel sind.
Dabei kannst du so vorgehen:
deiner Wahl berechnen, wie viel Prozent der Vögel Jungvögel, Vögel im 2. Lebensjahr oder Altvögel sind.
Dabei kannst du so vorgehen:
 der Altersgruppe
der Altersgruppe  an der Gesamtpopulation
an der Gesamtpopulation  :
:
 Dabei ist
Dabei ist  der Verteilungsvektor der stationären Verteilung, die du betrachtest.
1. Schritt: Verteilung und Gesamtpopulation berechnen
Wählst du zum Beispiel
der Verteilungsvektor der stationären Verteilung, die du betrachtest.
1. Schritt: Verteilung und Gesamtpopulation berechnen
Wählst du zum Beispiel  , dann ergibt sich der folgende Verteilungsvektor:
, dann ergibt sich der folgende Verteilungsvektor:
 Damit ist:
Damit ist:  ,
,  und
und  .
Die Gesamtpopulation ist dann also:
.
Die Gesamtpopulation ist dann also:  .
2. Schritt: Anteile der Altersgruppen berechnen
Nun kennst du alle Werte, die du benötigst und kannst diese nacheinander in die Formel einsetzen, um
.
2. Schritt: Anteile der Altersgruppen berechnen
Nun kennst du alle Werte, die du benötigst und kannst diese nacheinander in die Formel einsetzen, um  ,
,  und
und  zu berechnen:
zu berechnen:


 Für
Für  und die stationäre Verteilung
und die stationäre Verteilung  hat Altersgruppe 1 einen prozentualen Anteil an der Gesamtpopulation von ca.
hat Altersgruppe 1 einen prozentualen Anteil an der Gesamtpopulation von ca.  , Altersgruppe 2 hat einen Anteil von ca.
, Altersgruppe 2 hat einen Anteil von ca.  und Altersgruppe 3 einen Anteil von ca.
und Altersgruppe 3 einen Anteil von ca.  an der Gesamtpopulation.
an der Gesamtpopulation.
 Zeigen, dass sich für beliebiges
Zeigen, dass sich für beliebiges  die gleichen Anteile ergeben
Im vorherigen Aufgabenteil hast du bereits die prozentualen Anteile der einzelnen Altersgruppen für eine konkrete stationäre Verteilung berechnet. Nun sollst du zeigen, dass diese Anteile für jedes
die gleichen Anteile ergeben
Im vorherigen Aufgabenteil hast du bereits die prozentualen Anteile der einzelnen Altersgruppen für eine konkrete stationäre Verteilung berechnet. Nun sollst du zeigen, dass diese Anteile für jedes  gleich sind. Dazu kannst du genauso vorgehen wie eben, nur dass du nun nicht eine konkrete Verteilung wählst sondern die Verteilung abhängig von
gleich sind. Dazu kannst du genauso vorgehen wie eben, nur dass du nun nicht eine konkrete Verteilung wählst sondern die Verteilung abhängig von  belässt und so in die Formel einsetzt. Anschließend kannst du sehen, ob die prozentualen Anteile noch von
belässt und so in die Formel einsetzt. Anschließend kannst du sehen, ob die prozentualen Anteile noch von  abhängen oder nicht. Ist das der Fall, so ist der Anteil nicht bei jeder stationären Verteilung gleich, ansonsten sind sie für jede Altersgruppe immer gleich. Berechne dazu wieder
abhängen oder nicht. Ist das der Fall, so ist der Anteil nicht bei jeder stationären Verteilung gleich, ansonsten sind sie für jede Altersgruppe immer gleich. Berechne dazu wieder  ,
,  ,
,  und die Gesamtpopulation
und die Gesamtpopulation  , diesmal aber in Abhängigkeit von
, diesmal aber in Abhängigkeit von  .
1. Schritt: Verteilung und Gesamtpopulation berechnen
Für die Verteilung ergibt sich:
.
1. Schritt: Verteilung und Gesamtpopulation berechnen
Für die Verteilung ergibt sich:
 Damit ist:
Damit ist:  ,
,  und
und  .
Für die Gesamtpopulation ergibt sich damit:
.
Für die Gesamtpopulation ergibt sich damit:  .
2. Schritt: Anteile berechnen
Setze nun die Werte aus dem 1. Schritt wieder in die Formel ein, die du zuvor auch verwendet hast:
.
2. Schritt: Anteile berechnen
Setze nun die Werte aus dem 1. Schritt wieder in die Formel ein, die du zuvor auch verwendet hast:


 Die prozentualen Anteile der einzelnen Altersgruppen, sind nicht mehr abhängig von
Die prozentualen Anteile der einzelnen Altersgruppen, sind nicht mehr abhängig von  und daher für jede der angegebenen stationären Verteilungen gleich.
und daher für jede der angegebenen stationären Verteilungen gleich.

F5: G-Solv  F6
F6  F2: X-CAL
F2: X-CAL
bestimmen, indem du 

- Berechne für ein
, z.B.
, die Verteilung und die Gesamtpopulation
- Berechne den Anteil jeder Altersgruppe an der Gesamtpopulation mit Hilfe der Regeln für die Prozentrechnung
c) (1)  Übergangsmatrix angeben
Hier hast du nun den Übergangsgraphen gegeben, der die Entwicklung einer zweiten Seevogelart beschreibt und sollst ausgehend davon eine zugehörige Übergangsmatrix
Übergangsmatrix angeben
Hier hast du nun den Übergangsgraphen gegeben, der die Entwicklung einer zweiten Seevogelart beschreibt und sollst ausgehend davon eine zugehörige Übergangsmatrix  angeben.
angeben.
Überlege dir zunächst, wie viele Zeilen und spalten die Matrix haben muss. Anschließend kannst du dich um die Einträge von
haben muss. Anschließend kannst du dich um die Einträge von  kümmern.
Im Übergangsgraphen gibt es nur zwei Knoten, also kannst du davon ausgehen, dass es bei dieser Seevogelart nur zwei Altersgruppen gibt. Demnach muss die Übergangsmatrix jeweils zwei Zeilen und Spalten besitzen.
In Aufgabenteil a) (3) hast du gesehen, dass das Element
kümmern.
Im Übergangsgraphen gibt es nur zwei Knoten, also kannst du davon ausgehen, dass es bei dieser Seevogelart nur zwei Altersgruppen gibt. Demnach muss die Übergangsmatrix jeweils zwei Zeilen und Spalten besitzen.
In Aufgabenteil a) (3) hast du gesehen, dass das Element  die Übergangsquote von Altersgruppe
die Übergangsquote von Altersgruppe  in Altersgruppe
in Altersgruppe  beschreibt. In dem Übergangsgraphen findest du diese Quote als Bezeichnung an dem Pfeil vom Knoten
beschreibt. In dem Übergangsgraphen findest du diese Quote als Bezeichnung an dem Pfeil vom Knoten  zum Knoten
zum Knoten  .
Damit ergibt sich dann die folgende Übergangsmatrix:
.
Damit ergibt sich dann die folgende Übergangsmatrix:
 (2)
(2)  Entwicklung der 2. Seevogelart im Vergleich zur 1. beschreiben
Die Beschreibung der Entwicklung der 1. Seevogelart ist dir bereits in der Einführung zur Aufgabe gegeben. Überlege dir hier nun zunächst mit Hilfe des Übergangsgraphen, wie die Entwicklung der 2. Seevogelart abläuft und ziehe anschließend den Vergleich zur 1. Seevogelart.
1. Schritt: Entwicklung der zweiten Seevogelart beschreiben
Betrachte dazu zunächst den allgemeinen Aufbau des Graphen, also die Anzahl der Knoten, die Beschriftung der Knoten usw. Anschließend kannst du die Details betrachten, indem du dir über die Bedeutung der einzelnen Pfeile nacheinander Gedanken machst.
Am Graphen kannst du sehen, dass es bei der zweiten Seevogelart nur zwei Altersgruppen gibt. Da die Übergangsquoten sich wieder auf ein Jahr beziehen, bedeutet dies also, dass diese Seevogelart bereits nach einem Jahr ausgewachsen ist und die erste Brut bereits im zweiten Lebensjahr stattfinden kann.
Daran, dass der Pfeil von (1) nach (2) mit
Entwicklung der 2. Seevogelart im Vergleich zur 1. beschreiben
Die Beschreibung der Entwicklung der 1. Seevogelart ist dir bereits in der Einführung zur Aufgabe gegeben. Überlege dir hier nun zunächst mit Hilfe des Übergangsgraphen, wie die Entwicklung der 2. Seevogelart abläuft und ziehe anschließend den Vergleich zur 1. Seevogelart.
1. Schritt: Entwicklung der zweiten Seevogelart beschreiben
Betrachte dazu zunächst den allgemeinen Aufbau des Graphen, also die Anzahl der Knoten, die Beschriftung der Knoten usw. Anschließend kannst du die Details betrachten, indem du dir über die Bedeutung der einzelnen Pfeile nacheinander Gedanken machst.
Am Graphen kannst du sehen, dass es bei der zweiten Seevogelart nur zwei Altersgruppen gibt. Da die Übergangsquoten sich wieder auf ein Jahr beziehen, bedeutet dies also, dass diese Seevogelart bereits nach einem Jahr ausgewachsen ist und die erste Brut bereits im zweiten Lebensjahr stattfinden kann.
Daran, dass der Pfeil von (1) nach (2) mit  beschriftet ist, kannst du erkennen, dass die Übergangsquote, also sozusagen die Überlebensrate im 1. Lebensjahr,
beschriftet ist, kannst du erkennen, dass die Übergangsquote, also sozusagen die Überlebensrate im 1. Lebensjahr,  beträgt.
Analog dazu bedeutet der Pfeil von (2) zur (1) mit der Beschriftung
beträgt.
Analog dazu bedeutet der Pfeil von (2) zur (1) mit der Beschriftung  , dass ein Vogel im Durchschnitt jedes Jahr
, dass ein Vogel im Durchschnitt jedes Jahr  Nachkommen bekommt.
Der Pfeil von (2) zu (2) mit der Beschriftung
Nachkommen bekommt.
Der Pfeil von (2) zu (2) mit der Beschriftung  ist die Übergangsquote von Altersgruppe 2 nach Altersgruppe 2, also die Überlebensquote eines ausgewachsenen Vogels.
2. Schritt: Vergleich zwischen den beiden Arten
Vergleiche nun schrittweise die Entwicklungen der beiden Arten:
Dabei fällt dir folgendes auf:
ist die Übergangsquote von Altersgruppe 2 nach Altersgruppe 2, also die Überlebensquote eines ausgewachsenen Vogels.
2. Schritt: Vergleich zwischen den beiden Arten
Vergleiche nun schrittweise die Entwicklungen der beiden Arten:
Dabei fällt dir folgendes auf:
Überlege dir zunächst, wie viele Zeilen und spalten die Matrix
- Die 1. Seevogelart wird in drei Altersgruppen eingeteilt und ist erst nach zwei Jahren ausgewachsen und brutfähig, die 2. Seevogelart ist dagegen in nur zwei Altersgruppen eingeteilt worden und bereits nach dem ersten Lebensjahr ausgewachsen und brutfähig.
- Bei den Jungvögeln der 1. Seevogelart beträgt die Überlebensquote
, bei der 2. Art überleben weniger Jungtiere, hier beträgt die Überlebensquote
.
- Bei den Altvögeln, ist die Überlebensquote der 2. Seevogelart ebenfalls niedriger, diese beträgt
und die der 1. Art
.
- Der Bruterfolg ist allerdings bei der 2. Art höher: Hier bekommt jeder Altvogel durchschnittlich
Nachkommen pro Jahr, bei der 2. Art sind es
bzw. nach der Einführung der Schutzmaßnahmen
Nachkommen pro Vogel und pro Jahr.