Analysis 1

Für einen Tag wird die in einen Stausee zufließende Wassermenge betrachtet. Die momentane Zuflussrate wird durch die auf $\mathbb{R}$ definierte Funktion $f$ mit $f(x) = 0,005x^3-0,18x^2+1,55x+2$ für $0 \leq x \leq 24$ beschrieben.

Dabei gibt $x$ die Zeit nach Beobachtungsbeginn in Stunden $(h)$ und $f(x)$ die Zuflussrate des Wassers in 1000 Kubikmeter pro Stunde $\left(1000 \; \dfrac{\text{m}^3}{\text{h}} \right)$ an.
Der Stausee verfügt auch über einen künstlichen Wasserablauf. Es kann davon ausgegangen werden, dass der Ablauf am Tag der Beobachtung geschlossen ist.
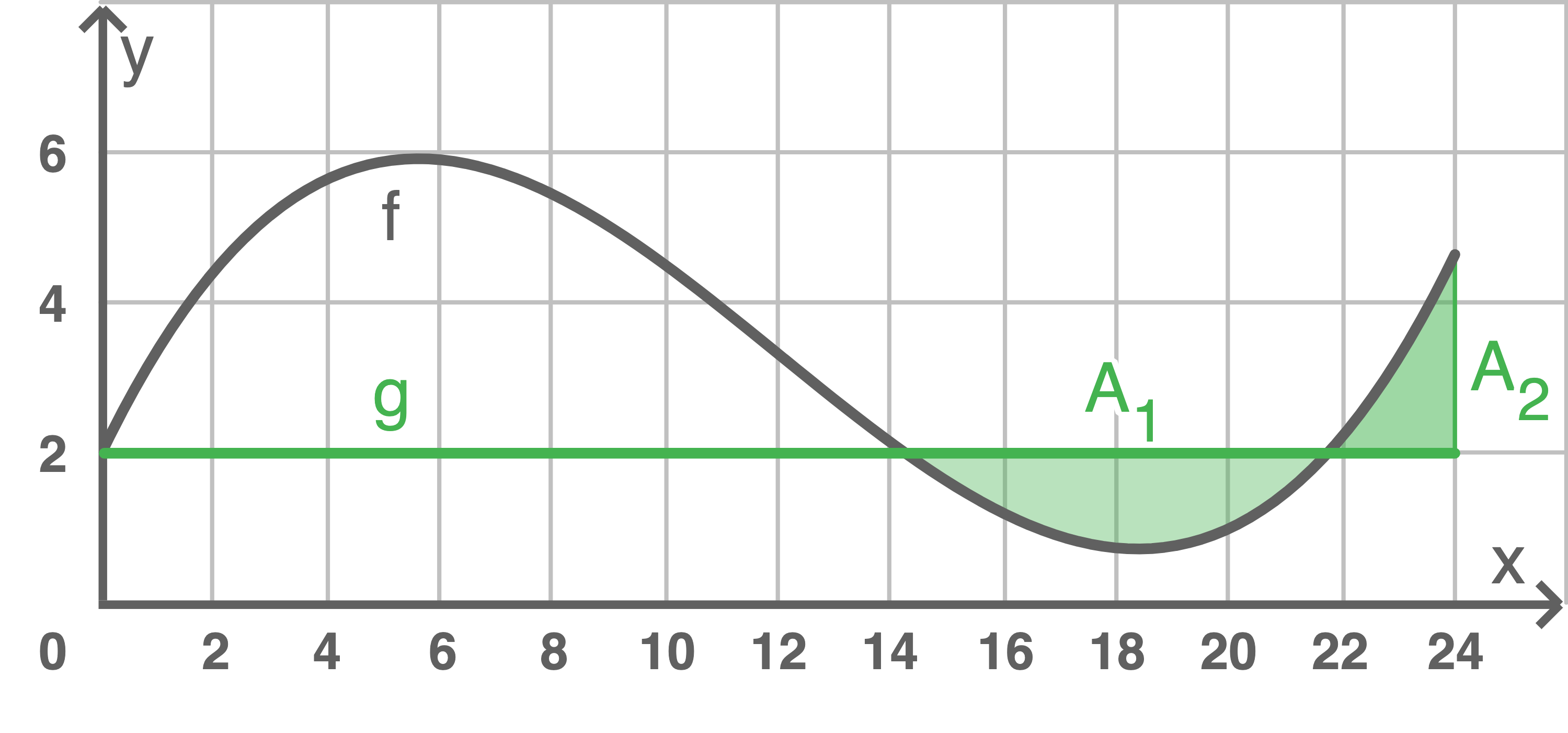
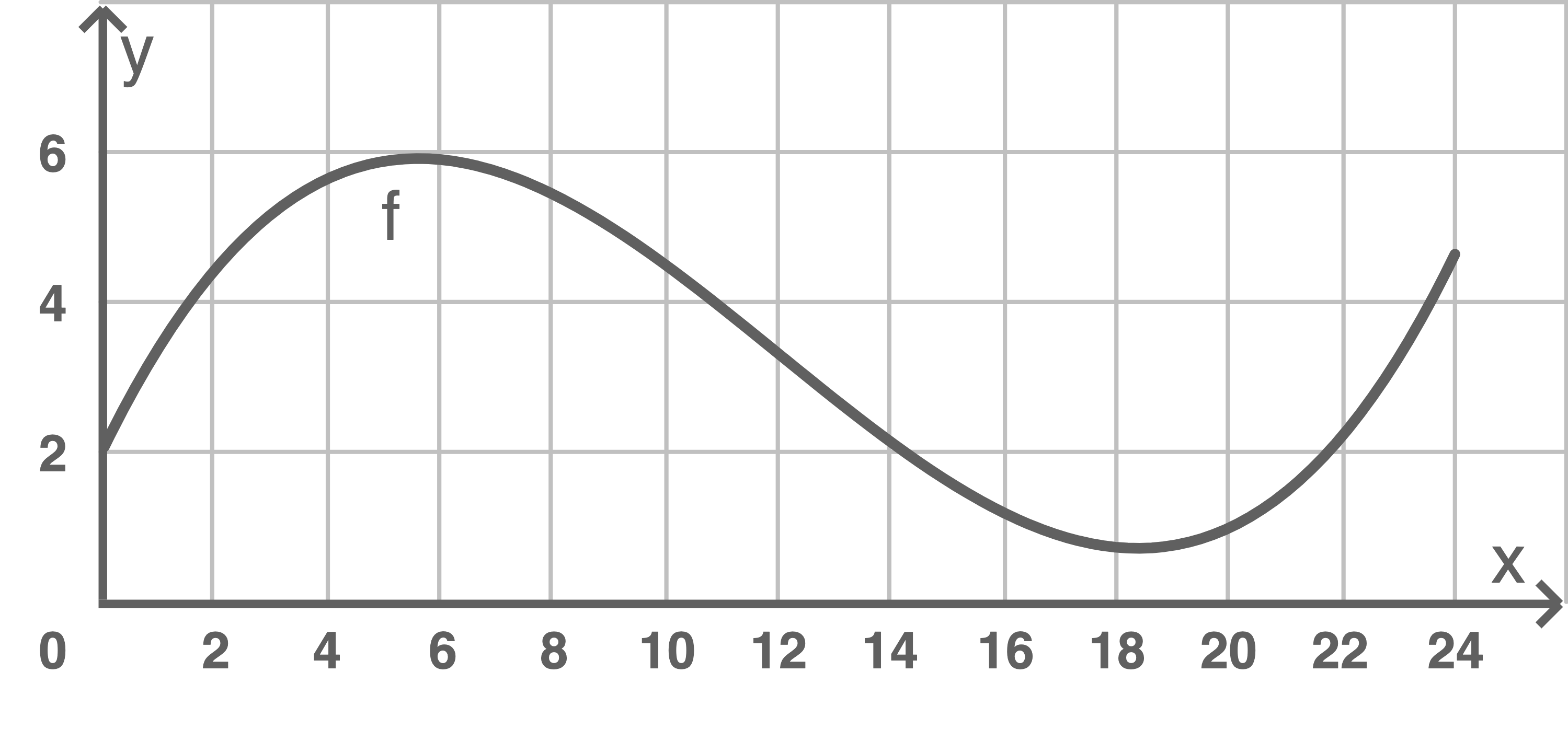
Die Abbildung stellt den Graphen der Funktion $f$ dar.

Gib $f(2)$ an und interpretiere den Wert im Sachzusammenhang.

Begründe mit Hilfe des Graphen von $f$ , dass der Wasserstand im Stausee ständig ansteigt.

(4 Punkte)

Berechne die Länge des Zeitraums, in dem die Zuflussrate geringer als $1000 ~\frac{\text{m}^3}{\text{h}}$ ist.

(3 Punkte)

Bestimme die maximale Zuflussrate im Beobachtungszeitraum.

(3 Punkte)

Bestimme die Zeitpunkte, an denen die Zuflussrate:

am stärksten abnimmt.
am stärksten zunimmt.

(5 Punkte)

Untersuche, ob es eine Zuflussrate gibt, die sich eine Stunde später verdoppelt hat.

(3 Punkte)

Vereinfacht wird die Form des Stausees als Quader mit einer Länge von $1000 \,\text{m}$ und einer Breite von $200 \,\text{m}$ angenommen.

Berechne das Volumen des Wassers, welches in den 24 Stunden nach Beobachtungsbeginn in den Stausee zugeflossen ist.

$[$ zur Kontrolle: $\; 79860 \,\text{m}^3]$

Ermittle den Anstieg der Wasserhöhe innerhalb der 24 Stunden.

(4 Punkte)

Von Beobachtungsbeginn bis zum Zeitpunkt $t$ ist eine bestimmte Wassermenge zugeflossen. In den folgenden drei Stunden fließt noch einmal genauso viel Wasser dazu.

Berechne den Zeitpunkt $t$ .

(4 Punkte)

Bei dem künstlichen Wasserablauf können konstante Abflussraten eingestellt werden.

6 Stunden nach Beobachtungsbeginn wird der Ablauf geöffnet.

Bestimme die Abflussrate des Stausees so, dass sich 24 Stunden nach Beobachtungsbeginn genauso viel Wasser im Stausee befindet wie zu Beobachtungsbeginn.

(4 Punkte)

Der Wasserablauf wird zu Beobachtungsbeginn mit einer Abflussrate von $2000 ~\frac{\text{m}^3}{\text{h}}$ geöffnet.

Begründe mit Hilfe einer Skizze im Graphen aus der Aufgabenstellung und ohne Rechnung, dass etwa zum Zeitpunkt $14,3 \,\text{h}$ die Wassermenge im Stausee maximal ist.

(5 Punkte)

(35 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$f(2)= 4,42$

Deutung im Sachzusammenhang:

Nach zwei Stunden beträgt die Zuflussrate des Wassers $4420 ~\dfrac{\,\text{m}^3}{\,\text{h}}.$

Ständiger Anstieg des Wasserstands begründen

Der Graph von $f$ gibt die Zuflussrate des Wassers an. Da $f(x)\gt 0$ für $0 \leq x \leq 24$ ist, fließt immer mehr Wasser dazu und der Wasserstand des Stausees steigt ständig an.

Schnittstellen des Graphen der Funktion $f$ mit der Geraden $y=1$ bestimmen:

$\begin{array}[t]{rll} f(x)&=& y & \\[5pt] 0,005 x^3-0,18 x^2+1,55 x+2 &=& 1 \end{array}$

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 5: intersect

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F6 $\to$ F2: X-CAL

Mit dem GTR ergeben sich die Schnittstellen $x_1 = 16,6$ und $x_2 = 20.$
Da $f(x)\lt 1$ für $16,6 \lt x \lt 20,$ ist die Zuflussrate in diesem Zeitraum kleiner als $1000 ~\dfrac{\,\text{m}^3}{\,\text{h}}.$
Die Länge des Zeitraums beträgt also $20-16,6 = 3,4 \; [\text{h}].$

Die maximale Zuflussrate entspricht dem Maximum des Graphen von $f.$ Dieses kann graphisch mit dem GTR bestimmt werden:

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 4: maximum

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F2: MAX

Die Koordinaten des Hochpunkts lauten $H(5,6\mid 5,9).$

Die maximale Zuflussrate wird also nach $5,6$ Stunden mit $5900 ~\dfrac{\,\text{m}^3}{\,\text{h}}$ erreicht.

Zeitpunkt der stärksten Abnahme bestimmen

Die Änderung der Zuflussrate entspricht der ersten Ableitung $\(f$ von $f.$

Die Zuflussrate nimmt also zu dem Zeitpunkt am stärksten ab, an dem der Graph von $\(f$ ein Minimum annimmt. Mit der graphischen Lösung des GTRs folgt:

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 3: minimum

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F3: MIN

Für die Extremstelle ergibt sich: $x_{\text{Min}}=12$

Die Zuflussrate nimmt also zwölf Stunden nach Beobachtungsbeginn am stärksten ab.

Zeitpunkt der stärksten Zunahme bestimmen

Analog zur stärksten Abnahme nimmt die Zuflussrate zu dem Zeitpunkt (an der Stelle) am stärksten zu, an dem der Graph von $\(f$ im Intervall $[0;24]$ ein Maximum annimmt.

Mit dem GTR kann die Ableitungsfunktion $\(f$ graphisch dargestellt werden. Es kann abgelesen werden, dass der Graph von $\(f$ im Intervall $[0;24]$ den größten Wert an den Intervallgrenzen annimmt.

Die Zuflussrate nimmt folglich zu Beobachtungsbeginn sowie 24 Stunden nach Beobachtungsbeginn am stärksten zu.

Gleichung aufstellen:

$2\cdot f(x)= f(x+1)$

Vollständige Gleichung anzeigen

Mit dem solve-Befehl des GTRs folgt:

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 5: intersect

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F6 $\to$ F2: X-CAL

Die Gleichung hat keine Lösung und somit schneiden sich die Graphen der beiden Funktionen im Intervall $[0;23]$ nicht.

Es existiert also keine Zuflussrate, die sich eine Stunde später verdoppelt hat.

Die zugeflossene Wassermenge im Stausee nach 24 Stunden ergibt sich aus:

Gleichung anzeigen

Der Wert des Integrals wird wie folgt berechnet:

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 7: $\int f(x)\;\mathrm dx$

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F6 $\to$ F3: $\int \;\mathrm dx$

Als Lösung ergibt sich $79,86.$ In den 24 Stunden nach Beobachtungsbeginn sind also $79860\,\text{m}^3$ Wasser in den Stausee zugeflossen.

Berechnen der Wasserhöhe:

$\dfrac{79860\,\text{m}^3}{1000\,\text{m} \cdot 200\,\text{m}}= 0,4\,\text{m}$

Der Anstieg der Wasserhöhe innerhalb der $24$ Stunden beträgt also $0,4\,\text{m}.$

Gesucht ist die Lösung folgender Gleichung:

$\begin{array}[t]{rll} \displaystyle\int_{0}^{t}f(x)\;\mathrm dx&=& \displaystyle\int_{t}^{t+3}f(x)\;\mathrm dx & \\[5pt] \end{array}$

Stammfunktion bilden:

$F(x)=0,0013x^4-0,06x^3+0,775x^2+2x$

Somit lassen sich die beiden Integrale wie folgt darstellen:

$\begin{array}[t]{rll} g&=& \displaystyle\int_{0}^{t}f(x)\;\mathrm dx& \\[5pt] &=& 0,0013t^4-0,06t^3+0,775t^2+2t \end{array}$

$h=\displaystyle\int_{t}^{t+3}f(x)\;\mathrm dx =...$

Vollständige Gleichung anzeigen

Mit dem GTR lassen sich die beiden Funktionen $g$ und $h$ graphisch darstellen. Durch Ablesen der Schnittstellen ergeben sich $t_1\approx -2,4$ und $t_2\approx 4,1.$

Da es sich um einen Zeitpunkt nach Beobachtungsbeginn handelt, kann $t_1$ ausgeschlossen werden.

Der gesuchte Zeitpunkt ist somit $t_2 \approx 4,1 \;[\text{h}].$

Da der Abfluss sechs Stunden nach Beobachtungsbeginn geöffnet wird, muss die gesamte Zuflussmenge der 24 Stunden in den verbleibenden 18 Stunden abfließen.

Die gesamte Zuflussmenge wurde in Teilaufgabe f bereits berechnet und ist somit durch $79860\,\text{m}^3$ gegeben.

Die Abflussrate innerhalb der 18 Stunden folgt nun mit $\dfrac{79860\,\text{m}^3}{18\,\text{h}}= 4400 ~\dfrac{\,\text{m}^3}{\,\text{h}}.$

Skizze Wasserablauf Stausee Mathe Abi GK

Die Gerade $g=2$ gibt die Abflussrate an. Im Intervall $[14,3; 21,7]$ verläuft der Graph von $f$ unterhalb des Graphen von $g.$ In diesem Zeitraum nimmt die Wassermenge im Stausee ab. Ansonten nimmt die Wassermenge innerhalb des Beobachtungszeitraums immer zu.

Der Inhalt der Fläche $A_1$ , die der Graph von $f$ mit dem Graphen von $g$ einschließt, gibt an, wieviel Wasser im Intervall $[14,3; 21,7]$ abfließt. Der Inhalt der Fläche $A_2$ gibt an, wieviel Wasser anschließend wieder bis zum Beobachtungsende zufließt.

Offenbar ist der Flächeninhalt der Fläche $A_1$ größer als der von $A_2.$ Ab dem Zeitpunkt $x_0 \approx 14,3$ fließt also mehr Wasser ab, als zufließt.

Die Wassermenge im Stausee ist also nach ungefähr $14,3$ Stunden maximal.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?