Aufgabe 5

Für ein Schwimmbad besitzen $2\,000$ Personen eine Jahreskarte. Für einen bestimmten Tag beschreibt die Zufallsgröße $X$ die Anzahl der Jahreskartenbesitzer, die das Schwimmbad besuchen. Vereinfachend soll davon ausgegangen werden, dass $X$ binomialverteilt ist. Dabei beträgt die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Jahreskartenbesitzer an diesem Tag das Schwimmbad besucht, $10\,\%.$

(1)

Es gilt $P(X=210)\approx 2,2\,\%.$

Interpretiere diese Aussage im Sachzusammenhang.

(2)

Bestimme die Wahrscheinlichkeit dafür, dass mehr als $210$ Jahreskartenbesitzer das Schwimmbad besuchen.

(3)

Bestimme die Wahrscheinlichkeit dafür, dass der Wert von $X$ höchstens um eine halbe Standardabweichung vom Erwartungswert der Zufallsgröße abweicht.

(4)

Bestimme die größte natürliche Zahl $k,$ für die die Wahrscheinlichkeit dafür, dass weniger als $k$ Jahreskartenbesitzer das Schwimmbad besuchen, kleiner als $10\,\%$ ist.

(5)

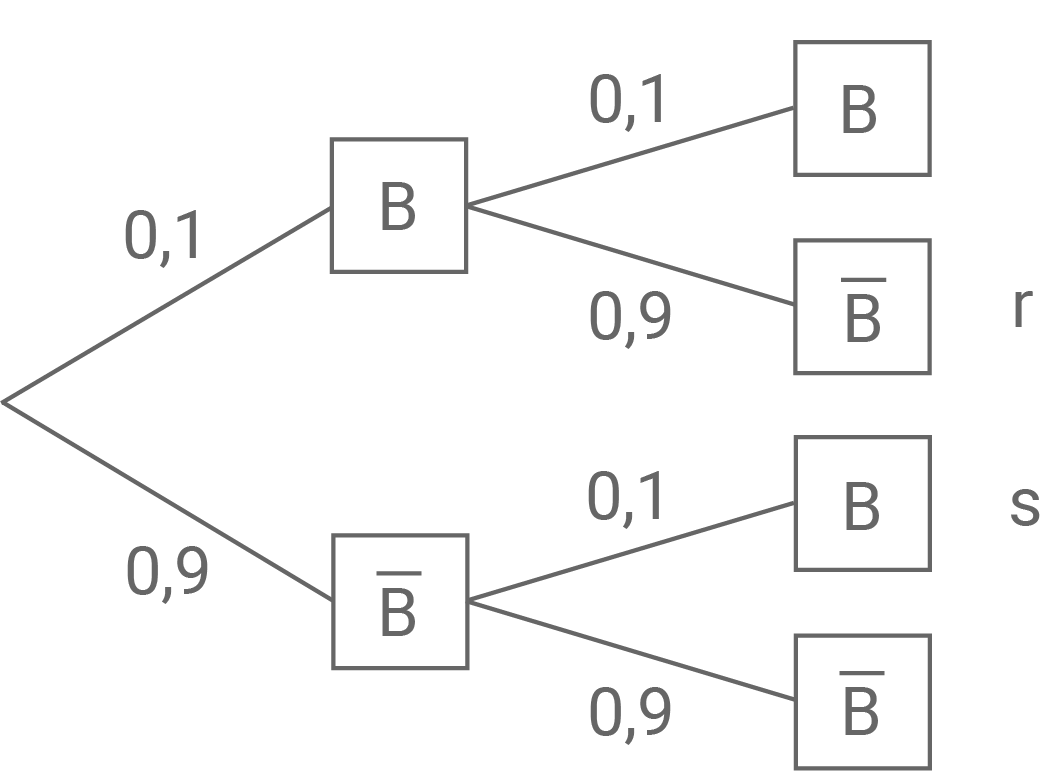
Beschreibe im Sachzusammenhang ein Zufallsexperiment, das durch das abgebildete Baumdiagramm dargestellt wird.
Gib ein Ereignis an, dessen Wahrscheinlichkeit $1-(r+s)$ beträgt.

Abbildung 1

(2 + 3 + 6 + 4 + 4 Punkte)

Abbildung 2 zeigt das Histogramm zu $P_{2000;0,1}(X=k).$

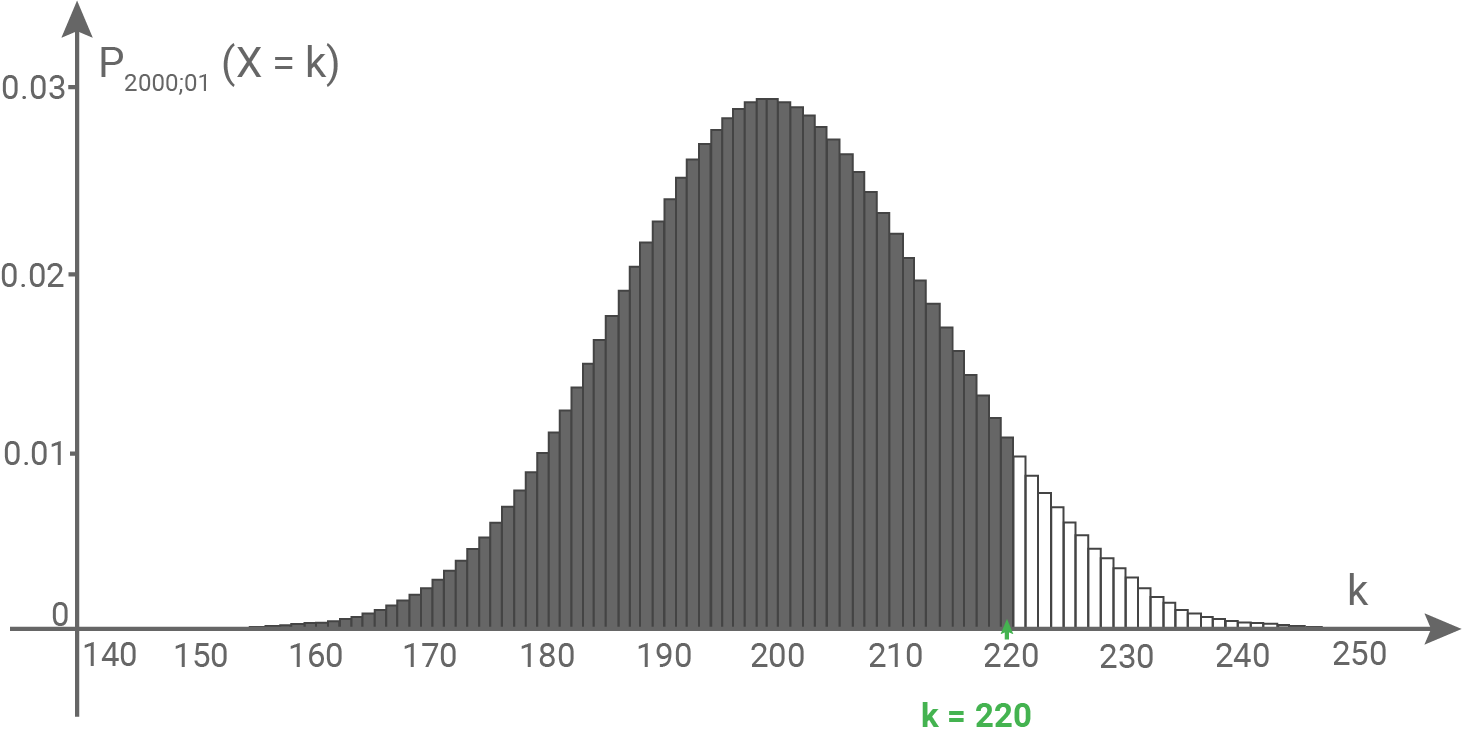
Abbildung 2

(1)

Beschreibe im Sachzusammenhang eine Fragestellung, die zu der in Abbildung 2 dargestellten Situation passt.

(2)

Bestimme die in Abbildung 1 dunkel dargestellte Wahrscheinlichkeit auf vier Nachkommastellen genau.

(3 + 2 Punkte)

Auf dem Gelände des Schwimmbades wird ein Kiosk betrieben. Der Besitzer nimmt vereinfachend an, dass jeder Gast $4\,€,$ $12\,€$ oder gar kein Geld an seinem Kiosk ausgibt. Die Wahrscheinlichkeit, dass ein Gast $4\,€$ ausgibt, betrage $50\,\%,$ die Wahrscheinlichkeit, dass ein Gast $12\,€$ ausgibt, betrage $30\,\%.$

(1)

An dem betrachteten Tag besuchen $660$ Personen das Bad. Bestimme die Höhe der Einnahmen, mit denen der Besitzer des Kiosks rechnen kann.

(2)

Ermittle die Wahrscheinlichkeit dafür, dass der Besitzer des Kiosks an dem betrachteten Tag erwartete Einnahmen von den Jahreskartenbesitzern hat, die mindestens $1000\,€$ betragen.

(3 + 4 Punkte)

Die Schwimmbadleitung hat die Außenanlagen komplett umgestaltet. Nun hofft sie, dass sich die Wahrscheinlichkeit dafür erhöht hat, dass ein zufällig ausgewählter Jahreskartenbesitzer an einem Tag, der mit dem in der Einleitung genannten vergleichbar ist, das Schwimmbad besucht. Daher zählt sie an einem solchen vergleichbaren Tag die Anzahl der Besucher mit Jahreskarte. Falls es $215$ oder mehr sind, will die Schwimmbadleitung davon ausgehen, dass die Umbaumaßnahmen wirksam waren.

(1)

$X$ sei die in a) betrachtete Zufallsgröße.
Ermittle $P_{2000;0,10}(X\geq 215)$ und erläutere die Bedeutung des Wertes im Sachzusammenhang.

(2)

Die getroffenen Maßnahmen mögen Erfolg gehabt haben. Die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Jahreskartenbesitzer an dem betrachteten Tag das Schwimmbad besucht, betrage nun $12\,\%.$ Für diesen Tag beschreibt die neue Zufallsgröße $Y$ die Anzahl der Jahreskartenbesitzer, die das Schwimmbad besuchen.
Dabei sei $p_{\text{neu}}=0,12$ und $n = 2000.$ Vereinfachend soll wieder davon ausgegangen werden, dass $Y$ binomialverteilt ist.
Ermittle die Wahrscheinlichkeit dafür, dass die Schwimmbadleitung in der vorliegenden Situation die Wirksamkeit der Umbaumaßnahmen falsch beurteilt.

(5 + 4 Punkte)

(1)

$\blacktriangleright$ Aussage im Sachzusammenhang interpretieren

Mit einer Wahrscheinlichkeit von ca. $2,2\,\%$ besuchen an einem bestimmten Tag genau $210$ Jahreskartenbesitzer das Schwimmbad.

(2)

$\blacktriangleright$ Wahrscheinlichkeit bestimmen

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ vars (distr) $\to$ B: binomcdf

$\blacktriangleright$ Casio fx-CG

Statistik: F5: DIST $\to$ F5: BINOM $\to$ F2: Bcd

$P(X\gt 210)\approx 21,6\,\%$

Vollständige Lösung anzeigen

Mit einer Wahrscheinlichkeit von ca. $21,6\,\%$ besuchen mehr als $210$ Jahreskartenbesitzer das Schwimmbad.

(3)

$\blacktriangleright$ Wahrscheinlichkeit bestimmen

Da $X$ binomialverteilt ist, folgt:

$\begin{array}[t]{rll} E(X)&=& 200\\[10pt] \sigma(X)&\approx& 13,4 \\[5pt] \end{array}$

Vollständige Lösung anzeigen

Für die Wahrscheinlichkeit folgt:

$...\approx 37,2\,\%$

Vollständige Lösung anzeigen

Mit einer Wahrscheinlichkeit von ca. $37,2\,\%$ weicht der Wert von $X$ um höchstens eine halbe Standardabweichung vom Erwartungswert der Zufallsgröße ab.

(4)

$\blacktriangleright$ Größtmögliche Zahl bestimmen

Gesucht ist das größte $k$ mit:

$P(X\lt k) \lt 0,1$

Berechne mit deinem GTR $P(X\lt k)$ für verschiedene Werte von $k.$ Du erhältst dann:

$...\approx 0,09$

Vollständige Lösung anzeigen

und

$...\approx 0,11$

Vollständige Lösung anzeigen

Also ist $k=183.$

(5)

$\blacktriangleright$ Zufallsexperiment beschreiben

Zwei der $2000$ Jahreskartenbesitzer werden zufällig ausgewählt und es wird überprüft, ob diese an diesem Tag das Schwimmbad besuchen.

$\blacktriangleright$ Ereignis mit der Wahrscheinlichkeit beschreiben

An dem betrachteten Tag besuchen entweder beide überprüften Jahreskartenbesitzer oder keiner von beiden das Schwimmbad.

(1)

$\blacktriangleright$ Fragestellung im Sachzusammenhang beschreiben

„Mit welcher Wahrscheinlichkeit besuchen an einem bestimmten Tag höchstens $220$ Jahreskartenbesitzer das Schwimmbad?“

(2)

$\blacktriangleright$ Wahrscheinlichkeit bestimmen

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ vars (distr) $\to$ B: binomcdf

$\blacktriangleright$ Casio fx-CG

Statistik: F5: DIST $\to$ F5: BINOM $\to$ F2: Bcd

Mit dem GTR erhältst du:

$P_{2\,000;0,1}(X\leq 220) \approx 0,9352$

(1)

$\blacktriangleright$ Höhe der erwarteten Einnahmen bestimmen

$... = 3.696\,€$

Vollständige Lösung anzeigen

Der Kioskbesitzer kann am betrachteten Tag mit Einnahmen in einer Höhe von $3.696\,€$ rechnen.

(2)

$\blacktriangleright$ Wahrscheinlichkeit ermitteln

Bezeichne die benötigte Anzahl an Jahreskartenbesitzern, die an dem Tag in das Schwimmbad kommen mit $n.$

$n\geq 178,57$

Vollständige Lösung anzeigen

Für die Wahrscheinlichkeit folgt mit dem GTR:

$P(X\geq 179) \approx 0,947 = 94,7\,\%$

Mit einer Wahrscheinlichkeit von ca. $94,7\,\%$ hat der Kioskbesitzer erwartete Einnahmen von den Jahreskartenbesitzern, die mindestens $1\,000\,€$ betragen.

(1)

$\blacktriangleright$ Wert ermitteln und Bedeutung erläutern

Mit dem GTR folgt $P_{2\,000;0,10}(X\geq 215) \approx 0,14$

Beträgt der Anteil der Jahreskartenbesitzer, die an einem bestimmten Tag das Schwimmbad besuchen weiterhin $10\,\%,$ so besuchen mit einer Wahrscheinlichkeit von ca. $14\,\%$ trotzdem mindestens $215$ Jahreskartenbesitzer an einem bestimmten Tag das Schwimmbad.
Nach der Beschreibung im Aufgabentext würde die Schwimmbadleitung in diesem Fall davon ausgehen, dass die Umbaumaßnahmen wirksam waren, obwohl sich die Wahrscheinlichkeit eigentlich nicht erhöht hat.

(2)

$\blacktriangleright$ Wahrscheinlichkeit ermitteln

Laut Aufgabenstellung soll vorausgesetzt werden, dass die neue Wahrscheinlichkeit tatsächlich $12\,\%$ beträgt.
$Y$ ist also binomialverteilt mit $n=2\,000$ und $p=0,12.$
Eine falsche Beurteilung erfolgt dann, wenn die Schwimmbadleitung davon ausgeht, dass die Umbaumaßnahmen nicht wirksam waren, obwohl sie es ja waren, da die Wahrscheinlichkeit gestiegen ist.
Die Schwimmbadleitung würde davon ausgehen, wenn an dem betrachteten Tag weniger als $215$ Jahreskartenbesitzer das Schwimmbad besuchen.

Mit dem GTR ergibt sich: $P_{2\,000;0,12}(Y\leq 214) \approx 0,038$

Mit einer Wahrscheinlichkeit von ca. $3,8\,\%$ beurteilt die Schwimmbadleitung die Wirksamkeit der Umbaumaßnahmen im beschriebenen Fall falsch.