A2

Eine Funktion $g$ ist gegeben durch die Gleichung $g(x)=\dfrac{1}{3}x^3-\dfrac{1}{2}x^2-6x+5,$ $x\in\mathbb{R}.$

(1)

Gib eine Funktionsgleichung der ersten Ableitung von $g$ an.

(2)

Berechne die Extremstellen von $g$ und die Art der Extremstellen.

(1 + 4 Punkte)

Gegeben sind die Funktion $f$ und $g$ mit den Gleichungen $f(x)=(x-3)\cdot\mathbb{e}^x,$ $x\in\mathbb{R},$ $g(x)=x-3,$ $x\in\mathbb{R}.$

Die Abbildung zeigt die Graphen der Funktion $f$ und $g.$

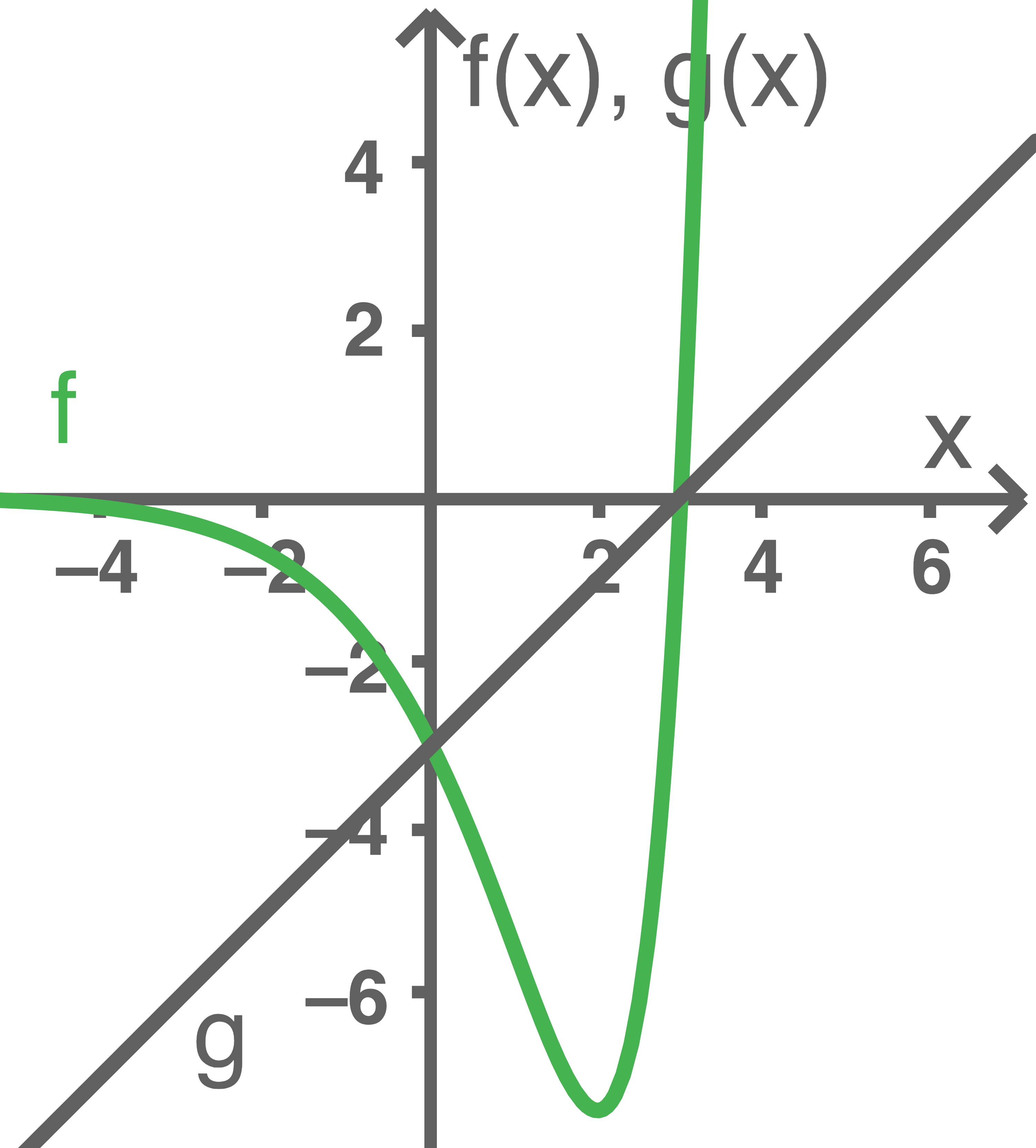
nrw mathe abi 2022 hilfsmittelfreier teil abbildung graph f und g

Abbildung 1

(1)

Gib die beiden Schnittstellen der Graphen der Funktionen $f$ und $g$ an.

(2)

Zeige: $D(x)=(4-x)\cdot\mathbb{e}^x+0,5\cdot x^2-3\cdot x$ ist eine Stammfunktion der Funktion $d$ mit $d(x)=g(x)-f(x)=(x-3)-(x-3)\cdot\mathbb{e}^x.$

(3)

Ermittle den Flächeninhalt der Fläche, die von den Graphen der Funktionen $f$ und $g$ eingeschlossen wird.

(1 + 2 + 2 Punkte)

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=x^2.$

Bestimme diejenige reelle Zahl $m$ mit $m\lt0,$ für die der Graph von $f$ und die Gerade mit der Gleichung $y=m\cdot x$ eine Fläche mit dem Inhalt $36$ einschließen.

(5 Punkte)

Pia hat eine Dartscheibe geschenkt bekommen. Sie trifft im Mittel zu etwa $80\,\%$ die Dartscheibe. Die Zufallsgröße $X:$ „Anzahl der Treffer beim Pfeilwurf auf die Dartscheibe“ wird im Folgenden als binomialverteilt mit $p = 0,8$ angenommen.
Pia wirft genau 100-mal auf die Dartscheibe.

(1)

Berechne den Erwartungswert und die Standardabweichung von $X.$

(2)

Gib einen Term zur Berechnung der Wahrscheinlichkeit an, dass Pia genau 80-mal die Dartscheibe trifft.

(3)

Gib einen Term zur Berechnung der Wahrscheinlichkeit an, dass sie mindestens einmal die Dartscheibe trifft, und begründe anhand des Terms, dass diese Wahrscheinlichkeit nahezu $100\,\%$ beträgt.

(2 + 1 + 2 Punkte)

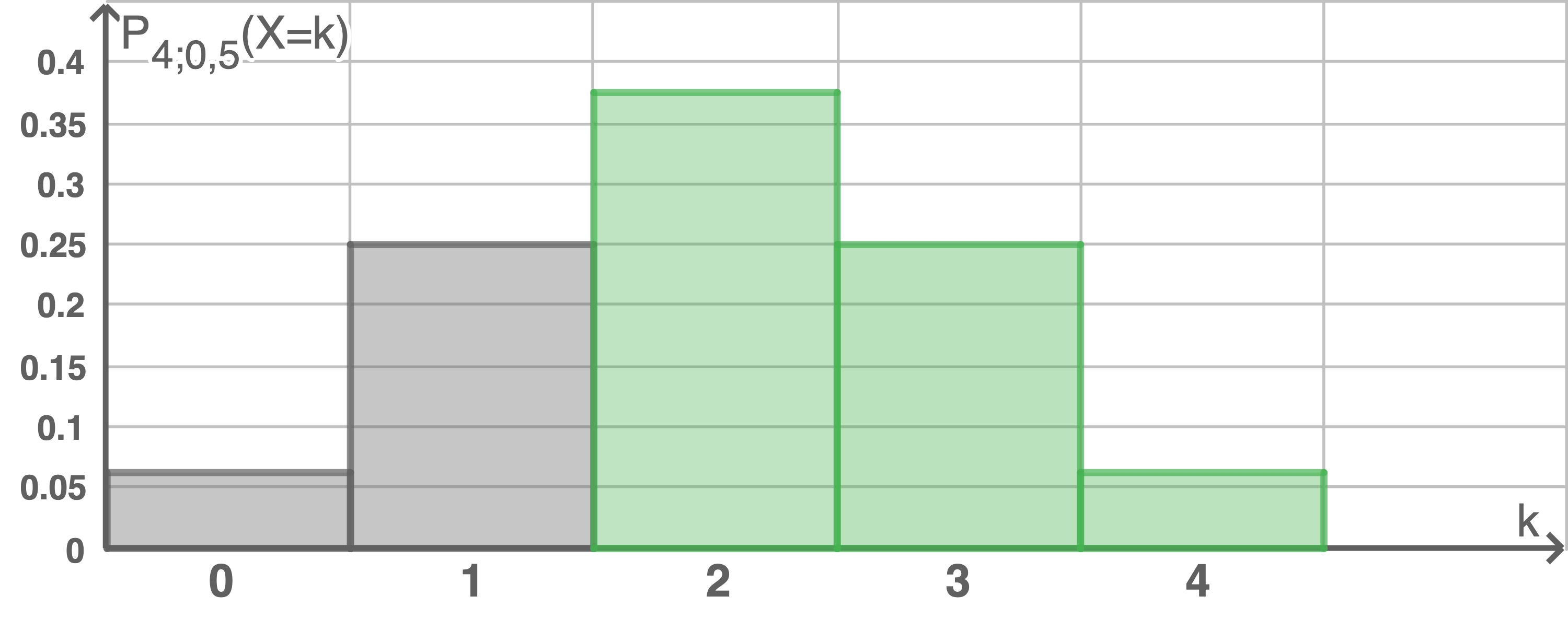
Abbildung 2 zeigt ein unvollständiges Histogramm einer binomialverteilten Zufallsgröße $X$ mit den Parametern $n=4$ und $p=0,5.$
Es gilt $P_{4;0,5}(X=0)=0,0625.$

Abbildung 2

Gib begründet $P_{4;0,5}(X=3)$ und $P_{4;0,5}(X=4)$ an.

Zeichne die fehlenden Säulen in Abbildung 2.

(5 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

(1)

Die Ableitung der Funktion lautet: $\(g$

(2)

1. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} g$

Mit der $pq$ -Formel folgt:

$\begin{array}[t]{rll} x_{1,2}&=&\dfrac{1}{2}\pm \sqrt{\left(\dfrac{-1}{2}\right)^2+6} & \\[5pt] &=&\dfrac{1}{2}\pm \sqrt{\dfrac{1}{4}+6} & \\[5pt] x_1&=&3 \\[5pt] x_2&=&-2 \end{array}$

2. Schritt: Hinreichende Bedingung für Extremstellen anwenden

Die zweite Ableitung der Funktion lautet: $\(g$

$\(g$

An der Stelle $x_1$ befindet sich ein Minimum und an der Stelle $x_2$ ein Maximum.

(1)

$\begin{array}[t]{rll} f(x)&=&g(x) &\\[5pt] (x-3)\cdot \mathrm e^x&=&x-3 & \\[5pt] \end{array}$

Für $x\neq 3$ gilt:

$\begin{array}[t]{rll} (x-3)\cdot \mathrm e^x&=&x-3 & \quad \scriptsize \mid\;:(x-3) \\[5pt] \mathrm e^x&=&1 &\quad \scriptsize \mid\; \ln \\[5pt] x_1&=&0 \end{array}$

Überprüfen für $x= 3$ :

$\begin{array}[t]{rll} (3-3)\cdot \mathrm e^3&=&3-3 &\\[5pt] 0&=&0 \end{array}$

Die Graphen der Funktionen $f$ und $g$ schneiden sich an den Stellen $x_1=0$ und $x_2=3$ .

(2)

Die Ableitung der Funktion $D(x)$ kann mit der Produktregel bestimmt werden.

$\(\begin{array}[t]{rll} D$

$d$ ist also eine Ableitung von $D$ , womit $D$ eine Stammfunktion von $d$ ist.

(3)

Rechenweg anzeigen

$A=\mathrm e^3-8,5 \;\text{[FE]}$

Der Flächeninhalt der Fläche der von den Graphen der Funktionen $f$ und $g$ eingeschlosen wird, beträgt $A=\mathrm e^3-8,5 \;\text{[FE]}$ .

Die gesuchte Fläche wird von den Graphen der beiden Funktionen und deren Schnittstellen eingegrenzt.

1. Schritt: Bestimmung der Schnittstellen

$\begin{array}[t]{rll} f(x)&=&y \\[5pt] x^2&=&m\cdot x &\quad \scriptsize \mid\;-m\cdot x \\[5pt] x^2-m\cdot x&=&0 &\\[5pt] x \cdot (x-m)&=&0&\\[5pt] \end{array}$

Mit Hilfe des Satzes vom Nullprodukt kann die Gleichung mit $x_1=m$ und $x_2=0$ gelöst werden.

2. Schritt: Berechnung des Flächeninhalts der eingeschlossenen Fläche

Rechenweg anzeigen

$A=-\dfrac{1}{6} m^3$

3. Schritt: Bestimmung von $m$

$\begin{array}[t]{rll} A&=&36\\[5pt] -\dfrac{1}{6}m^3&=&36 &\quad \scriptsize \mid\; \cdot (-6)\\[5pt] m^3&=&-6^3 &\quad \scriptsize \mid\; \sqrt[3]{\;}\\[5pt] m&=&-6 \end{array}$

(1)

Der Erwartungwert ergibt sich als: