Teil A2
a)
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  .
.
(1)
Einer der folgenden Graphen I, II und III stellt  dar.
dar.
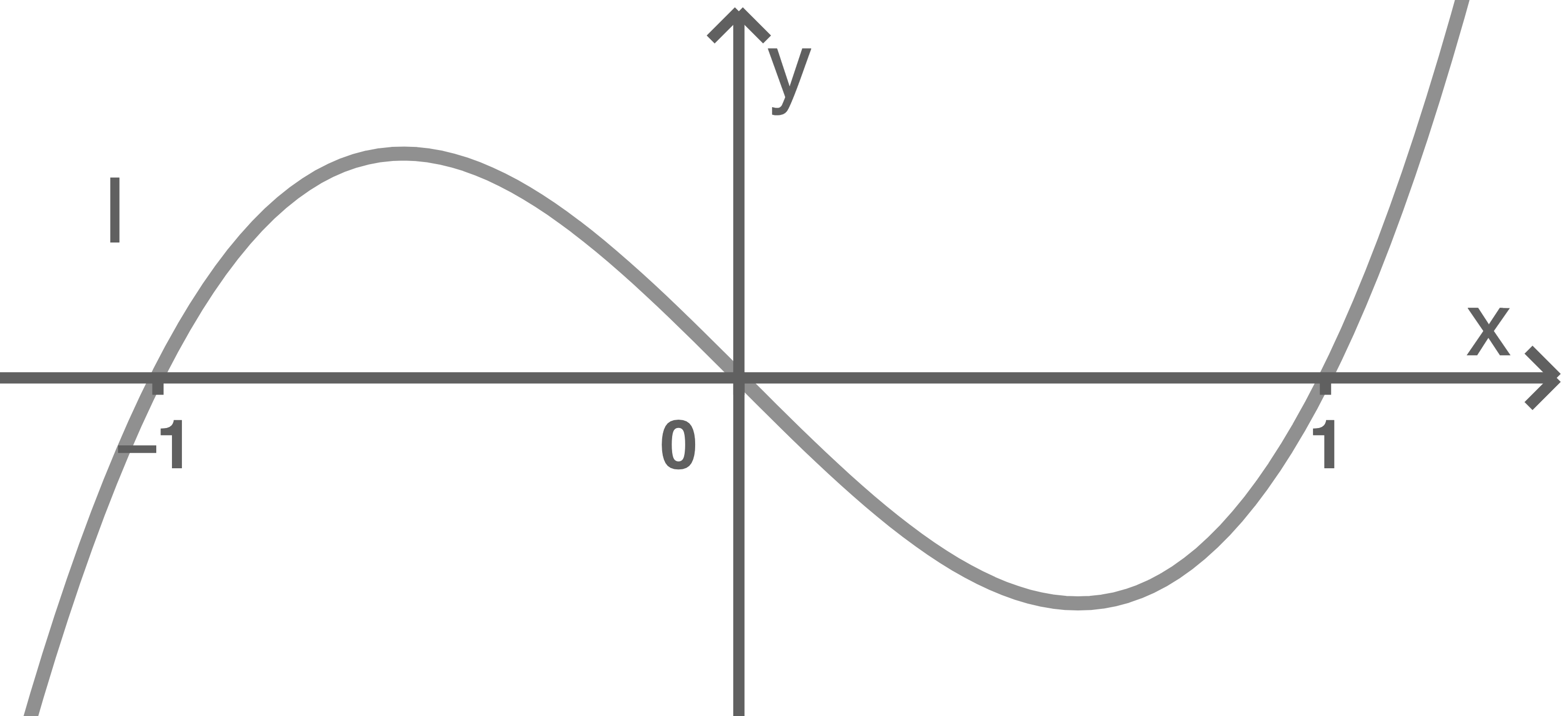
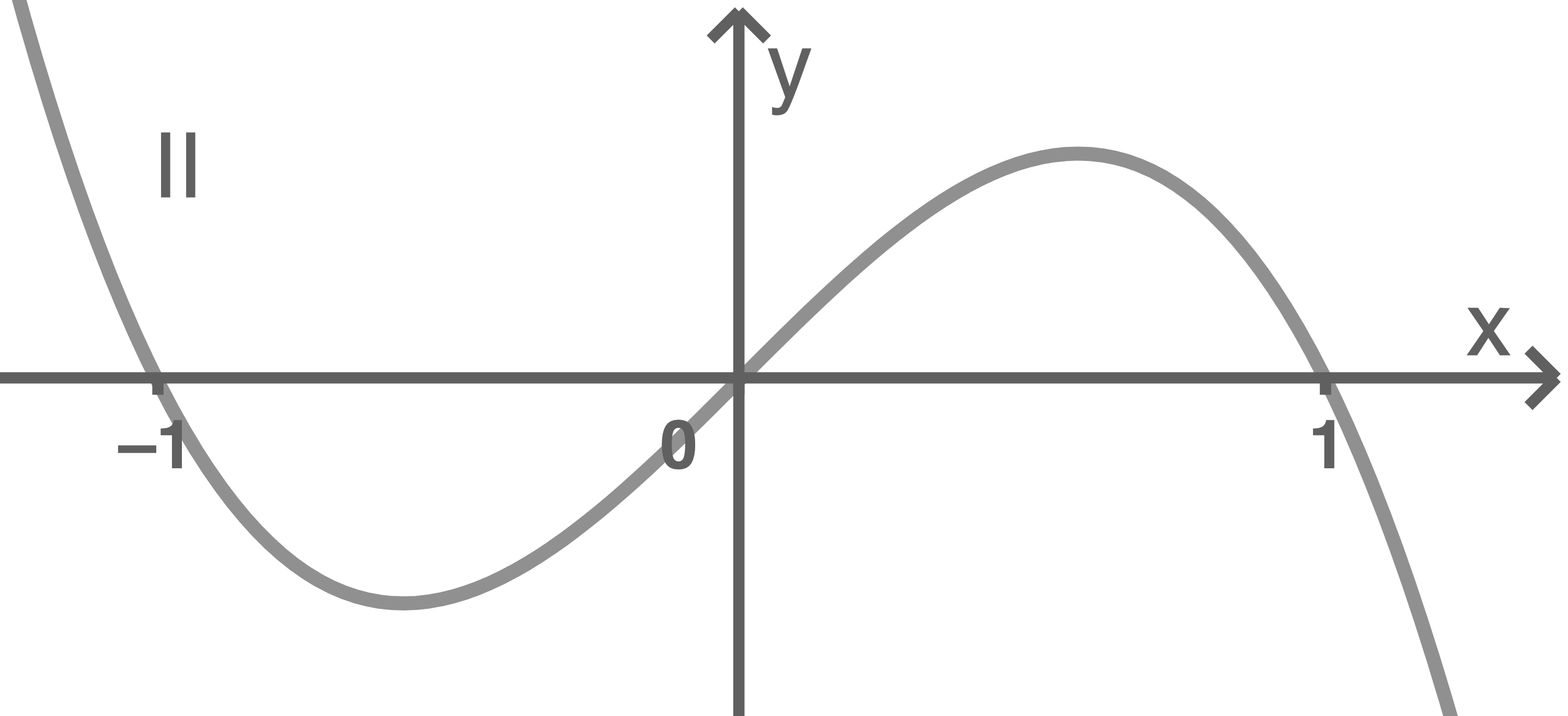
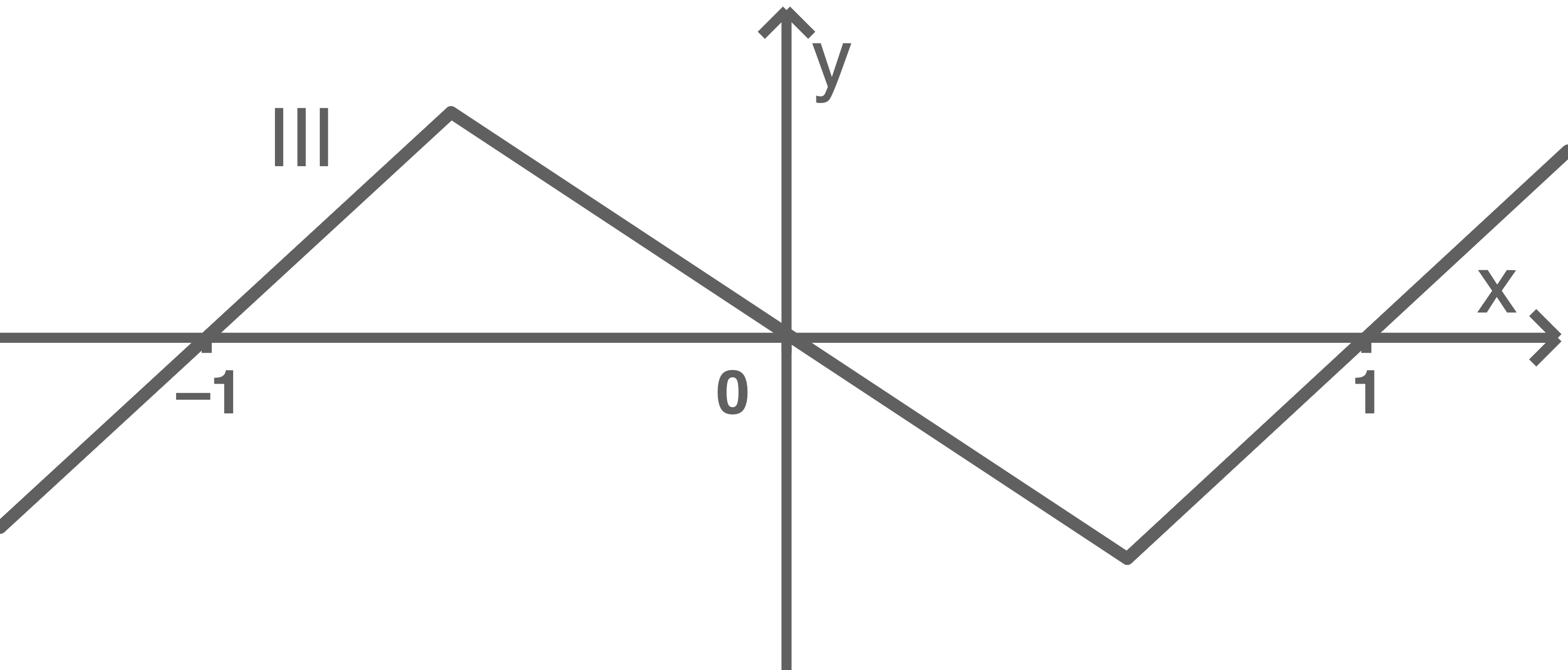 Gib die Graphen an, die dafür nicht infrage kommen, und begründe deine Angabe.
Gib die Graphen an, die dafür nicht infrage kommen, und begründe deine Angabe.



Abbildung 1
(2)
Berechne den Inhalt der Fläche, die der Graph von  und die
und die  -Achse einschließen.
Hinweis: Die Nullstellen dürfen dabei der obigen Abbildung 1 entnommen werden.
-Achse einschließen.
Hinweis: Die Nullstellen dürfen dabei der obigen Abbildung 1 entnommen werden.
(2 + 3 Punkte)
b)
Gegeben ist die Funktion  mit
mit  ,
,  .
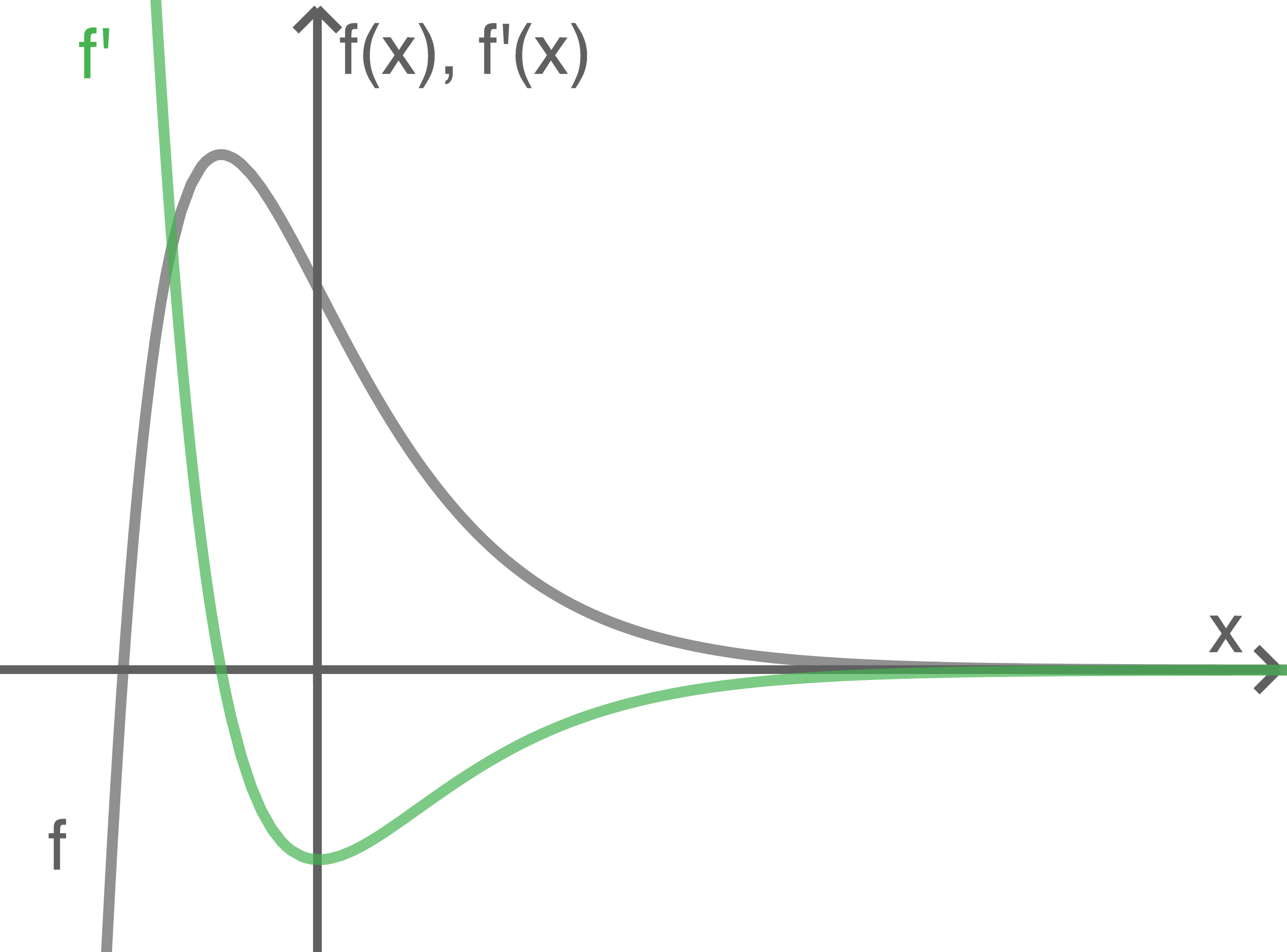
Der Graph von
.
Der Graph von  ist in Abbildung 2 dargestellt.
ist in Abbildung 2 dargestellt.
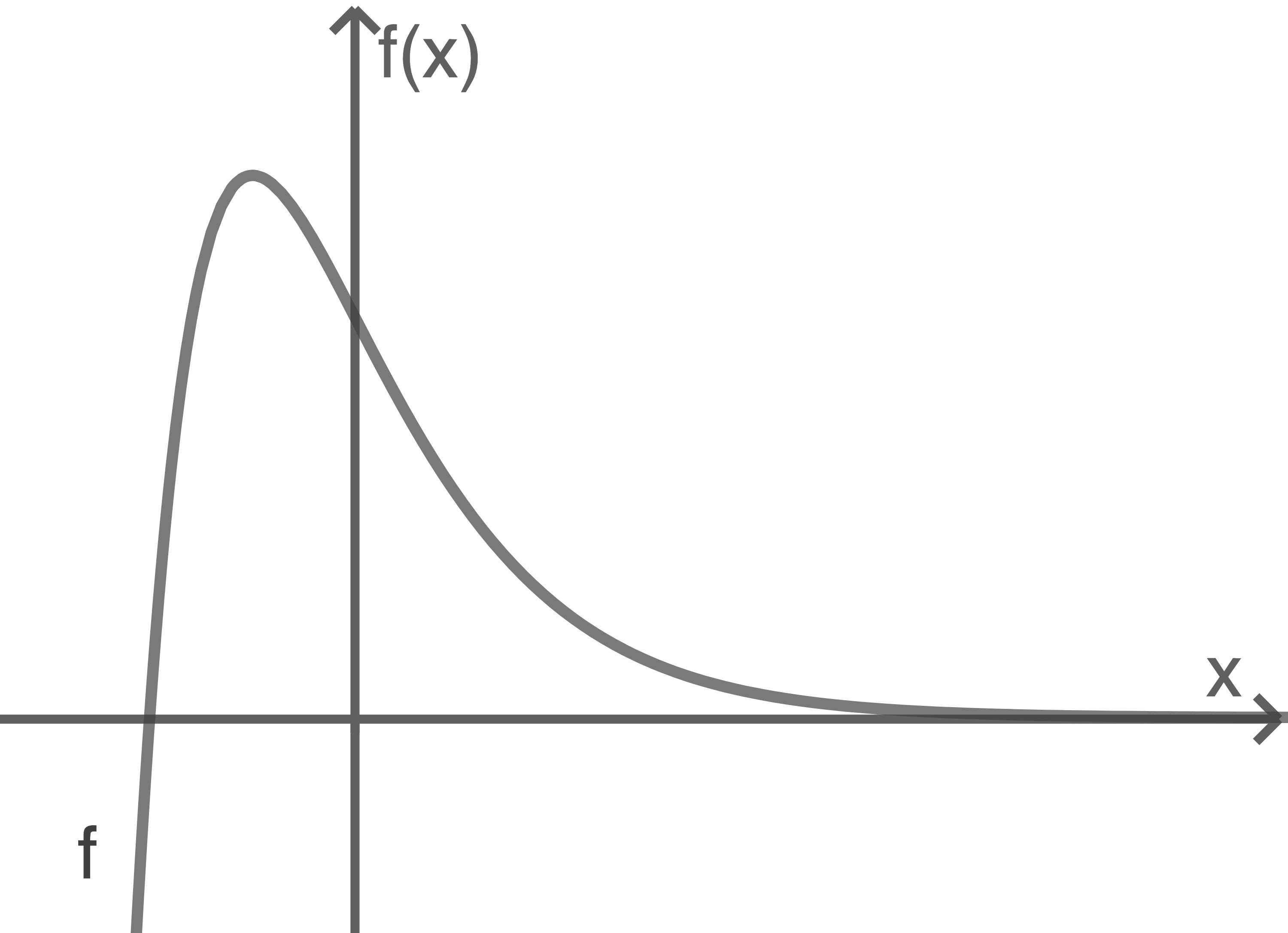

Abbildung 2
(1)
Die Funktion  besitzt genau eine Extremstelle.
Ermittle die Extremstelle von
besitzt genau eine Extremstelle.
Ermittle die Extremstelle von  Hinweis: Ein Nachweis der hinreichenden Bedingung ist nicht erforderlich.
Hinweis: Ein Nachweis der hinreichenden Bedingung ist nicht erforderlich.
(2)
Skizziere in Abbildung 2 den Graphen der Ableitungsfunktion von  Hinweis: Die Größe der
Hinweis: Die Größe der  -Werte kann dabei unberücksichtigt bleiben.
-Werte kann dabei unberücksichtigt bleiben.
(3 + 2 Punkte)
c)
Für jedes 
 ist durch die Gleichung
ist durch die Gleichung
 ,
,  ,
eine Funktion
,
eine Funktion  gegeben.
gegeben.
(1)
Gib die Nullstellen der Funktion  mit
mit  an.
an.
(2)
In Abbildung 3 ist der Graph der Funktion  für ein konkretes
für ein konkretes  abgebildet.
Begründe, dass für den Graphen in Abbildung 3 gilt:
abgebildet.
Begründe, dass für den Graphen in Abbildung 3 gilt:  .
.
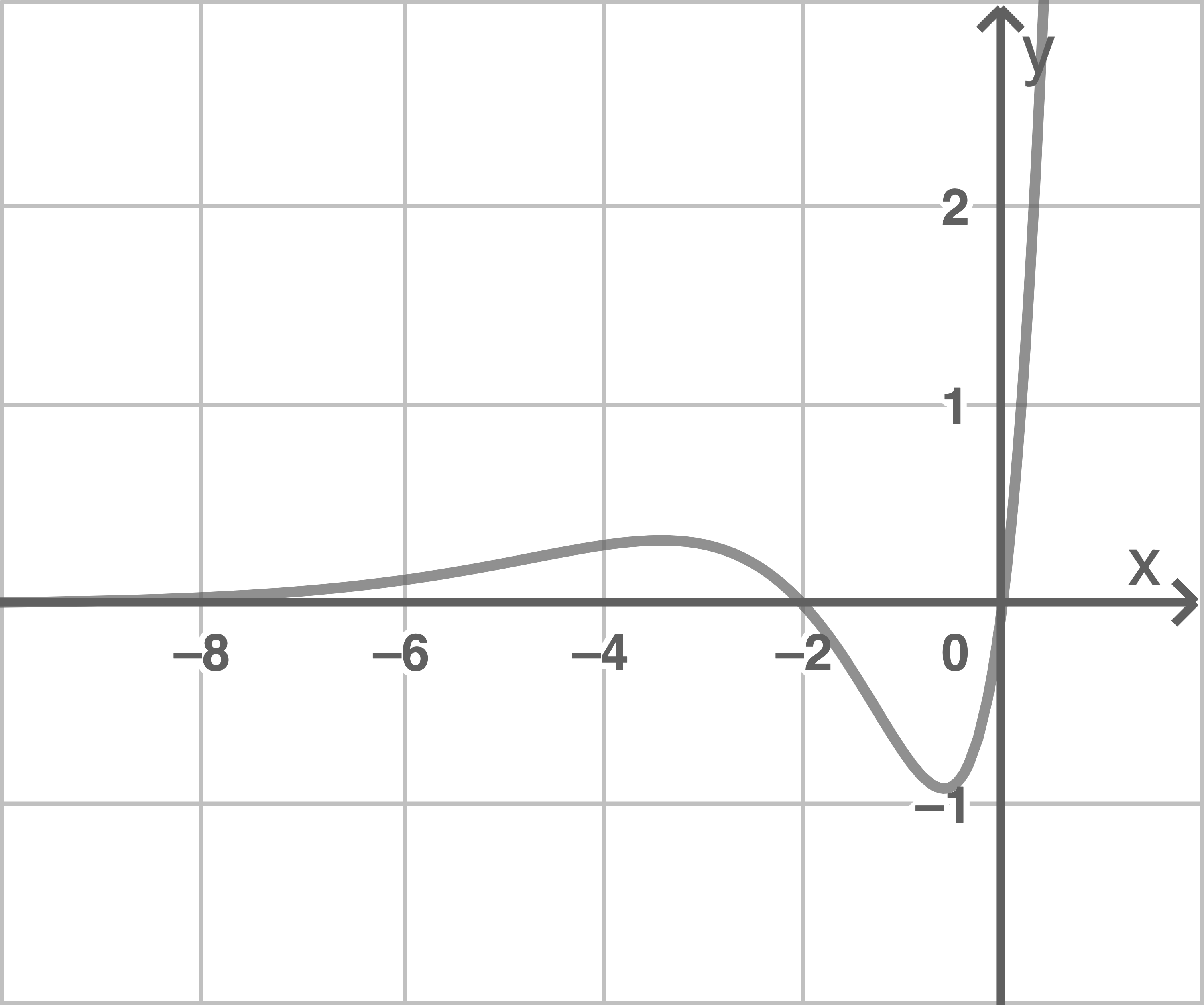

Abbildung 3
(3)
Ermittle, für welchen Wert von  der Punkt
der Punkt  auf dem Graphen der Funktion
auf dem Graphen der Funktion  liegt.
liegt.
(1 + 2 + 2 Punkte)
d)
Die Zufallsgröße  ist binomialverteilt mit den Parametern
ist binomialverteilt mit den Parametern  und
und 
Die Wahrscheinlichkeitsverteilung von ist symmetrisch zum Erwartungswert.
ist symmetrisch zum Erwartungswert.
Die Wahrscheinlichkeitsverteilung von
(1)
Berechne den Erwartungswert und die Standardabweichung von  .
.
(2)
Die Wahrscheinlichkeit  beträgt etwa
beträgt etwa  Bestimme unter Verwendung dieses Wertes den zugehörigen Wert für die Wahrscheinlichkeit
Bestimme unter Verwendung dieses Wertes den zugehörigen Wert für die Wahrscheinlichkeit  .
.
(3 + 2 Punkte)
e)
Im Folgenden werden zwei Würfel stets gemeinsam geworfen. Bei jedem der beiden Würfel sind die Seiten mit den Zahlen von  bis
bis  durchnummeriert.
durchnummeriert.
(1)
Die beiden Würfel werden einmal geworfen.
Begründe, dass die Wahrscheinlichkeit dafür, dass dabei keine  auftritt,
auftritt,  beträgt.
beträgt.
(2)
Die beiden Würfel werden  -mal geworfen. Die binomialverteilte Zufallsgröße
-mal geworfen. Die binomialverteilte Zufallsgröße  gibt die Anzahl der Würfe an, bei denen keine
gibt die Anzahl der Würfe an, bei denen keine  auftritt.
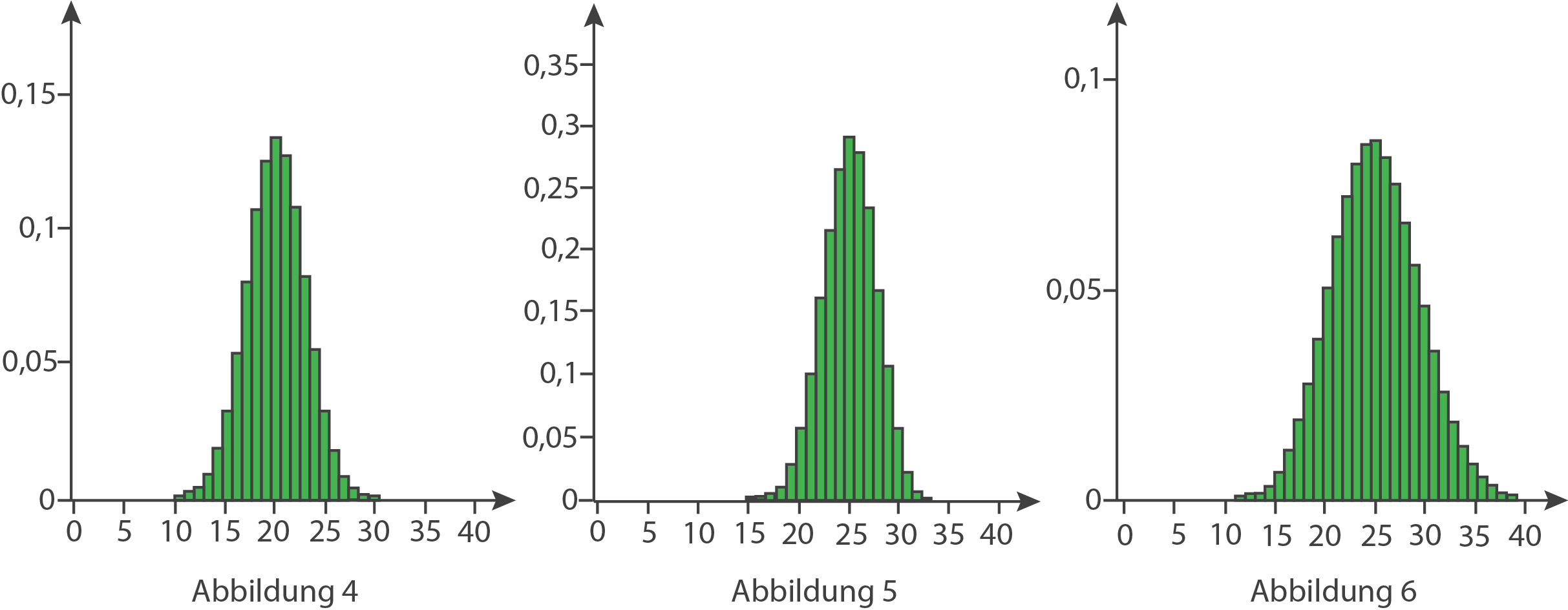
Begründe für jede der folgenden Abbildungen
auftritt.
Begründe für jede der folgenden Abbildungen 
 und
und  dass sie nicht die Wahrscheinlichkeitsverteilung von
dass sie nicht die Wahrscheinlichkeitsverteilung von  zeigt.
zeigt.

(2 + 3 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
(1)
Der Verlauf des Graphens richtet sich immer nach dem höchsten Exponenten.
Die Graphen II und III kommen nicht infrage, denn Graph III stellt keine ganzrationale Funktion dar und Graph II entspricht dem Graphen der Funktion
Die Graphen II und III kommen nicht infrage, denn Graph III stellt keine ganzrationale Funktion dar und Graph II entspricht dem Graphen der Funktion
(2)
Der Graph von  schließt mit der
schließt mit der  -Achse zwei gleich große Flächen ein. Da Graph I punktsymmetrisch zum Koordinatenursprung ist, reicht es, nur eine der beiden eingeschlossenen Flächen zu berechnen und diese dann zu verdoppeln.
-Achse zwei gleich große Flächen ein. Da Graph I punktsymmetrisch zum Koordinatenursprung ist, reicht es, nur eine der beiden eingeschlossenen Flächen zu berechnen und diese dann zu verdoppeln.


![\(=2\cdot\left[\dfrac{1}{4}x^4-\dfrac{1}{2}x^2\right]_{-1}^0=2\cdot\left(-\dfrac{1}{4}+\dfrac{1}{2}\right)
\)](https://mathjax.schullv.de/1b2dec9c120662d32f4326a27f6d8d64ad0849dacd891d865bb2304e3ae98afd?color=5a5a5a)

b)
(1)
(2)
c)
(1)
Nullstellen angeben
![\(\begin{array}[t]{rll}
f_1(x)&=&0 &\quad \scriptsize \\[5pt]
(x+2)(2x+1)\cdot \mathrm e^x &=& 0&\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/92fbe9f48304e0e45f2e4bb43c4173557913e943061cf9985c029044bd5325c7?color=5a5a5a) Es ist
Es ist  Mit dem Satz vom Nullprodukt folgt
Mit dem Satz vom Nullprodukt folgt  oder
oder  Daraus folgt die erste Nullstelle mit
Daraus folgt die erste Nullstelle mit  und die zweite mit:
und die zweite mit:
![\(\begin{array}[t]{rll}
2x+1 &=& 0 &\quad \scriptsize \mid\;-1 \mid\;:2 \\[5pt]
x_2&=& -\dfrac{1}{2}
\end{array}\)](https://mathjax.schullv.de/fe65c9da0cdc76f1d4b140a609add28aeea70721c8102854f68f3eb311c77c47?color=5a5a5a)
(2)
1. Schritt: Nullstellen von  angeben
angeben
![\(\begin{array}[t]{rll}
f_a(x)&=&0 &\quad \scriptsize \\[5pt]
(x+2)(2x+a)\cdot \mathrm e^x &=& 0&\quad \scriptsize \\[5pt]
\end{array}\)](https://mathjax.schullv.de/64ba5691361237ce8ed5956adbe5de6ec637295900c430d6a2e1a528f9c45459?color=5a5a5a) Es ist
Es ist  Mit dem Satz vom Nullprodukt folgt
Mit dem Satz vom Nullprodukt folgt  oder
oder  Die Nullstellen von
Die Nullstellen von  folgen daraus mit
folgen daraus mit  und
und  2. Schritt: Nullstellen der Abbildung
Der Graph in der Abbildung hat die Nullstellen
2. Schritt: Nullstellen der Abbildung
Der Graph in der Abbildung hat die Nullstellen  und
und 
Daraus folgt, dass gilt.
gilt.
Daraus folgt, dass
(3)
d)
(1)
Erwartungswert
 Standardabweichung
Standardabweichung


(2)
Da  gilt, ist die Wahrscheinlichkeitsverteilung von
gilt, ist die Wahrscheinlichkeitsverteilung von  symmetrisch zum Erwartungswert
symmetrisch zum Erwartungswert  daraus folgt
daraus folgt 
e)
(1)
Die Wahrscheinlichkeit keine 6 zu würfeln beträgt  Bei zwei Würfen hintereinander beträgt die Wahrscheinlichkeit mit der Pfadmultiplikationsregel
Bei zwei Würfen hintereinander beträgt die Wahrscheinlichkeit mit der Pfadmultiplikationsregel 
(2)
Der höchste Balken stellt den Erwartungswert dar. Bei  Würfen und der Wahrscheinlichkeit
Würfen und der Wahrscheinlichkeit  ergibt sich der Erwartungswert von
ergibt sich der Erwartungswert von  mit
mit  Auf keiner der abgebildeten Abbildungen entspricht der höchste Balken einem Wert von 25.
Abbildung 4: Die höchste Säule befindet sich bei 20.
Abbildung 5: Die Summe der Höhen der Säulen ist größer als 1.
Abbildung 6: Die Höhe der Säule bei 37 ist größer als null.
Auf keiner der abgebildeten Abbildungen entspricht der höchste Balken einem Wert von 25.
Abbildung 4: Die höchste Säule befindet sich bei 20.
Abbildung 5: Die Summe der Höhen der Säulen ist größer als 1.
Abbildung 6: Die Höhe der Säule bei 37 ist größer als null.