Aufgabe 3

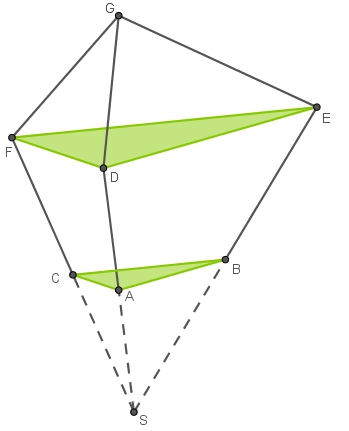
Das Gebäude eines Museums kann modellhaft durch den abgebildeten Körper $ABCDEFG$ dargestellt werden.
Die obere Etage entspricht dabei der Pyramide $DEFG,$ die untere Etage dem Körper $ABCDEF,$ der Teil der Pyramide $DEFS$ ist. Die Ebene, in der das Dreieck $ABC$ liegt, beschreibt die horizontale Oberfläche des Untergrunds. Das Dreieck $DEF$ liegt parallel zu dieser Ebene.
In einem kartesischen Koordinatensystem gilt für die Lage einiger der genannten Punkte:

$A(-5\mid 5\mid 0),$ $B(-5\mid 25\mid 0),$ $D(0\mid 0\mid 15),$ $E(0\mid 30\mid 15),$ $F(-25\mid 5\mid 15)$ und $G(-10\mid 10\mid 35).$

Eine Längeneinheit im Koordinatensystem entspricht $1\,\text{m}$ in der Realität.

nrw mathe abi 2022 hilfsmittelfreier teil abbildung graph f und g

Abbildung 1

Die folgenden Rechnungen zeigen ein mögliches Vorgehen zur Ermittlung der Koordinaten von $S:$

Rechnung anzeigen

d.h. $S(-15\mid 15\mid -30)$

Erläutere das dargestellte Vorgehen.

(5 Punkte)

(1)

Weise nach, dass die Bodenfläche $DEF$ der oberen Etage nicht rechtwinklig ist.

(4 Punkte)

$\,$

(2)

Bestimme für das Dreieck $DEF$ die Größe des Innenwinkels $\epsilon$ bei $E.$

[Zur Kontrolle: $\epsilon = 45^{\circ}$ ]

(3 Punkte)

$\,$

(3)

Im Dreieck $DEF$ ist der Punkt $P$ der Fußpunkt der Höhe $h$ auf die Seite $\overline{EF}$ (vgl. Abbildung 2).

Abbildung 2: nicht maßstabsgetreu

Begründe, dass das Dreieck $DEP$ gleichschenklig ist, und bestimme die Länge der Höhe $h.$

[Zur Kontrolle: $h=15\sqrt{2}$ ]

(5 Punkte)

$\,$

(4)

Begründe, dass der Abstand des Punktes $G$ zur Ebene durch $DEF$ direkt aus den $x_3$ -Koordinaten der entsprechenden Punkte ermittelt werden kann, und gib diesen Abstand an.

(3 Punkte)

$\,$

(5)

Für die obere Etage wird eine Anlage zur Entfeuchtung der Luft installiert, die für $100\,\text{m}^3$ Rauminhalt eine elektrische Leistung von $0,8$ Kilowatt benötigt.
Weise nach, dass für den Betrieb der Anlage eine Leistung von $25$ Kilowatt ausreichend ist.

(5 Punkte)

Die obere Etage wird durch einen Laser alarmgesichert.
Der Laser ist im Punkt $Q(-9\mid 8\mid 15,5)$ an einer Metallstange befestigt. Diese Metallstange verläuft geradlinig von der Spitze $G$ der Pyramide über den Punkt $Q$ zur Bodenfläche der oberen Etage.

(1)

Ermittle die Koordinaten des Bodenpunktes $R$ der Metallstange in der Bodenfläche und die Länge der Metallstange.

Hinweis: Ein Nachweis, dass der Punkt $R$ innerhalb des Dreiecks $DEF$ liegt, wird nicht erwartet.

(7 Punkte)

$\,$

(2)

Der Laser im Punkt $Q$ ist so eingestellt, dass der Lichtstrahl in Richtung des Vektors $\overrightarrow{v}$ mit $\overrightarrow{v}= \pmatrix{0,34\\0,84\\0,02}$ ausgerichtet ist.
Zeige, dass der Lichtstrahl mit dieser Einstellung auf die Kante $\overline{GE}$ trifft.

(8 Punkte)

$\blacktriangleright$ Vorgehen beschreiben

Der Punkt $S$ ist der Schnittpunkt der drei Geraden durch die Punkte $F$ und $C,$ $D$ und $A,$ $E$ und $B.$

Es genügt den Schnittpunkt zweier Geraden zu bestimmen. In der dargestellten Rechnung werden die beiden Parameterdarstellungen der Geraden durch die Punkte $D$ und $A$ mit dem Geradenparameter $r$ und durch die Punkte $E$ und $B$ mit dem Geradenparameter $s$ gleichgesetzt.
Diese Gleichung liefert eine Lösung für $r$ und $s.$ Der Wert für $r$ wird in die Geradengleichung durch die Punkte $D$ und $A$ eingesetzt und liefert den Ortsvektor des Schnittpunkts.
Daraus erhält man die Koordinaten des Punkts $S.$

(1)

$\blacktriangleright$ Nachweisen, dass die Bodenfläche nicht rechtwinklig ist

Die Bodenfläche $DEF$ ist rechtwinklig, wenn es zwei Verbindungsvektoren der Eckpunkte gibt, die senkrecht aufeinander stehen. Das ist der Fall, wenn ihr Skalarprodukt Null ist.

$\begin{array}[t]{rll} \overrightarrow{DE}\circ \overrightarrow{DF}& \neq 0 \\[10pt] \overrightarrow{DE}\circ \overrightarrow{EF}&\neq 0 \\[10pt] \overrightarrow{DF}\circ \overrightarrow{EF}& \neq 0 \\[10pt] \end{array}$