Analysis 2

Mit einem Pflaster können einer Person durch die Haut Medikamente zugeführt werden, z.B. Hormone. Diese Pflaster geben über einen langen Zeitraum hinweg Hormone ab.

Eine Arzneimittelfirma hat solche Pflaster an Personen getestet, deren körpereigene Hormonproduktion lediglich $50 \,\%$ des Sollwertes beträgt. Der Sollwert liegt bei $100 \,\%$ .

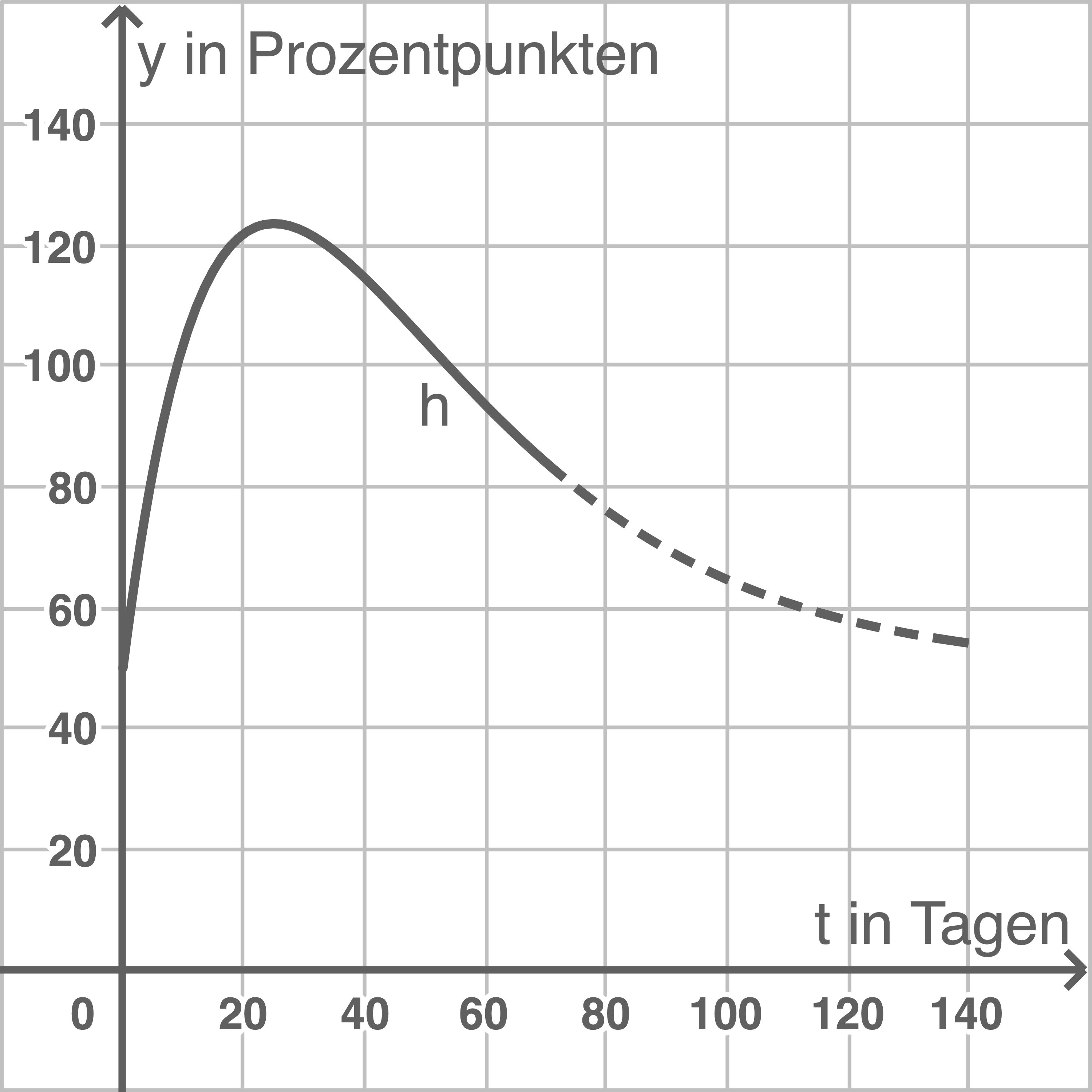
Bei der Messung der Hormonwerte zeigt sich, dass die Messergebnisse durch folgende Funktion $h$ beschrieben werden können:

$h(t)=8t\cdot \mathrm e^{-0,04\cdot t}+50\; ; \; t\geq 0$

Dabei ist $t$ die Zeit in Tagen ab Beginn der Behandlung.

Die Funktionswerte von $h$ werden als Hormonspiegel bezeichnet.
Der Hormonspiegel gibt in Abhängigkeit von $t$ den Anteil bezüglich des Sollwerts in Prozent an.

Funktionswerte größer als $100$ sind möglich, wenn der Hormonwert über dem Sollwert liegt.

Hormonpflaster Prozentpunkte Sollwert Muster-Abi 2 NRW

Untersuche das Verhalten der Funktionswerte von $h$ für $t \mapsto + \infty.$

Ermittle, wann der maximale Wert des Hormonspiegels erreicht wird und berechne diesen Wert. Es genügt die Verwendung der notwendigen Bedingung.

(5 Punkte)

Wenn der Hormonspiegel stark abfällt, werden vermehrt Nebenwirkungen beobachtet.

Ermittle den Zeitpunkt, an dem der Hormonspiegel am stärksten fällt.

Berechne für diesen Zeitpunkt den Wert des Hormonspiegels.

Gib für diesen Zeitpunkt die lokale Änderungsrate in $\,\%$ pro Tag an.

Berechne die mittlere Änderungsrate des Hormonspiegels in den ersten sieben Tagen nach Beginn der Behandlung.

(5 Punkte)

Weise nach, dass $\dfrac{1}{70}\cdot\displaystyle\int_{0}^{70}h(t)\;\mathrm dt\gt 100$ gilt.

(2 Punkte)

Bei einem Patienten wird das Pflaster nach $70$ Tagen entfernt. Der Hormonspiegel kann danach durch eine Gerade $g$ beschrieben werden, die im Punkt $p (70 \mid h(70))$ tangential zum Graphen von $h$ verläuft.

Ermittle eine Gleichung für $g$ .

$[$ Kontrollergebnis: $g(t)\approx -0,88 \cdot t +145,4]$

Untersuche im Sachzusammenhang, ab welchem Zeitpunkt eine Beschreibung des Hormonspiegels durch die Gerade $g$ nicht mehr sinnvoll sein kann.

(5 Punkte)

Der durch das Hormonpflaster über den Wert 100 ansteigende Hormonspiegel soll bei manchen Patienten vermieden werden.

Ermittle, wann ein solcher Patient das Pflaster entfernen sollte und gib an, wie viele Tage er sonst einen Hormonspiegel von 100 oder mehr hätte.

(4 Punkte)

Patienten, deren Hormonspiegel den Wert 100 nicht übersteigen soll, erhalten die Anweisung, das Pflaster am 10. Tag zu entfernen. Ihr Hormonspiegel nimmt ab diesem Moment exponentiell gemäß der Funktion $f(t)=a\cdot \mathrm e^{b\cdot t}$ ab und erreicht bereits am $30.$ Tag den Wert $h(70)$ .

Gib $h(10)$ an und beurteile die Höhe des Hormonspiegels $h(10)$ hinsichtlich eines möglichen Risikos für diese Patienten.

Begründe, dass für die Funktion $f$ die beiden Bedingungsgleichungen $I$ und $II$ für $a$ und $b$ erfüllt werden müssen:

$\begin{array}{lrll} \text{I:}\quad&a\cdot \mathrm e ^{10b} &\approx& 104 \\ \text{II:}\quad&a \cdot \mathrm e^{30b}&\approx& 84 \\ \end{array}$

Berechne $a$ und $b$ und gib den Funktionsterm $f(t)$ an.

(8 Punkte)

Der Hersteller möchte die Wirkstoffmenge in den Pflastern erhöhen und geht davon aus, dass der Hormonspiegel dann durch eine Funktion $h_k$ mit folgender Gleichung beschrieben werden kann:

$h_k(t)=k\cdot t \cdot \mathrm e^{-0,04 \cdot t}+50 \; ; \; t\geq 0$ und $k\geq 0$

Ermittle, ab welchem Wert von $k$ der Hormonspiegel am 70. Tag noch mindestens den Wert 100 erreicht.

(3 Punkte)

Vergleiche den Verlauf des Graphen von $h(t)=8t \cdot \mathrm e ^ {-0,04 \cdot t}+50$ mit einem Graphen von $h_k(t)=k\cdot t \cdot \mathrm e^{-0,04\cdot t}+50$ für einen frei wählbaren Wert von $k$ mit $k\gt 8$ und nenne mindestens drei Gemeinsamkeiten oder Unterschiede, die beim Vergleich auffallen.

(35 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Verhalten der Funktionswerte untersuchen

Für $t\to +\infty$ gilt:

$\lim\limits_{t\to\infty}h(t)=\lim\limits_{t\to\infty}8t\cdot \underbrace{\mathrm e^{\underbrace{-0,04\cdot t}_{\to -\infty}}}_{\to 0} +50=50$

Maximalen Wert berechnen

Der maximale Wert des Hormonspiegels entspricht dem Hochpunkt der Funktion $h.$

1. Schritt: Ableitung bilden

Mit dem CAS kann die Ableitung $\(h$ von $h$ gebildet werden:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 1: Ableitung

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\frac{d}{d \Box}\Box$

Es folgt: $\(h$

2. Schritt: Notwendiges Kriterium für Extremstellen anwenden

$\(\begin{array}[t]{rll} h$

Mit dem solve-Befehl des CAS folgt $t=25.$

Da in der Aufgabenstellung angegeben ist, dass die Anwendung der notwendigen Bedingung genügt, kann davon ausgegangen werden, dass dies die Stelle mit dem maximalen Funktionswert ist.

25 Tage nach Beginn der Behandlung ist somit der maximale Wert des Hormonspiegels erreicht.

3. Schritt: Maximalen Wert berechnen

$\begin{array}[t]{rll} h(25) &=& 8\cdot 25 \cdot \mathrm e^{-0,04\cdot 25}+50 \\[5pt] &\approx& 123,58 \end{array}$

Der maximale Wert des Hormonspiegels beträgt also etwa 123,58 Prozentpunkte und wird 25 Tage nach Beginn der Behandlung erreicht.

Zeitpunkt der stärksten Abnahme bestimmen

Die momentane Änderungsrate des Hormonspiegels wird durch die erste Ableitungsfunktion $\(h$ beschrieben. Gesucht ist also das Minimum der Funktion $h‘.$

Notwendige Bedingung anwenden:

$\(\begin{array}[t]{rll} h$

Mit dem solve-Befehl des CAS folgt $t=50.$

Da in der Aufgabenstellung bereits gegeben ist, dass ein Minimum der Änderungsrate existiert, ist die Untersuchung der hinreichenden Bedingung für ein Minimum nicht mehr nötig.

50 Tage nach Beginn der Behandlung fällt also der Wert des Hormonspiegels am stärksten.

Wert des Hormonspiegels berechnen

$\begin{array}[t]{rll} h(50) &=& 8\cdot 50 \cdot \mathrm e^{-0,04\cdot 50} +50 \\[5pt] &\approx& 104,13 \end{array}$

Zu dem Zeitpunkt, zu dem der Wert des Hormonspiegels am stärksten abfällt, beträgt der Wert des Hormonspiegels ca. 104,13 Prozentpunkte.

Lokale Änderungsrate angeben

Die lokale Änderungsrate wird durch die Funktion $\(h$ beschrieben:

$\begin{array}[t]{rll} h‘(50)&=& (8-0,32\cdot 50)\cdot \mathrm e^{-0,04\cdot 50} \\[5pt] &\approx& -1,08 \end{array}$

Zu dem Zeitpunkt, zu dem der Wert des Hormonspiegels am stärksten abfällt, fällt der Hormonspiegel um ca. $1,08$ Prozentpunkte pro Tag.

Mittlere Änderungsrate berechnen

Die mittlere Änderungsrate lässt sich mithilfe des Differenzenquotienten berechnen:

Rechenweg anzeigen

$\overline{m}\approx 6,05$

In den ersten sieben Tagen nach Beginn der Behandlung beträgt die mittlere Änderungsrate des Hormonspiegels etwa $6,05$ Prozentpunkte pro Tag.

Der Wert des Integrals kann mit dem CAS berechnet werden:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 3: Integral

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\int_{\Box}^{\Box}\Box$

Es folgt:

$\dfrac{1}{70}\cdot \displaystyle\int_{0}^{70}h(t)\;\mathrm dt \approx 104,9$

Rechenweg anzeigen

Gleichung ermitteln

Allgemeine Geradengleichung: $y=m\cdot x+c$

Die Tangente im Punkt $p(70\mid h(70))$ hat die gleiche Steigung wie der Graph von $h$ in diesem Punkt.

Es gilt also:

$\(\begin{array}[t]{rll} m&=& h$

$y$ -Koordinate von $p$ bestimmen:

$h(70) = 560 \cdot \mathrm e^{-2,8} +50$

Durch eine Punktprobe kann nun $b$ berechnet werden:

$b=1568\cdot \mathrm e^{-2,8} +50$

Rechnung anzeigen

Eine Gleichung für $g$ ist also:

$g(t) \approx -0,88t + 145,4$

Rechenweg anzeigen

Zeitpunkt untersuchen

Die Pflaster werden an Personen getestet, deren körpereigene Hormonproduktion lediglich $50\,\%$ des Sollwertes beträgt. Sobald die Modellierung also unter 50 Prozentpunkte fällt, ist die Beschreibung durch die Gerade nicht mehr sinnvoll.

$\begin{array}[t]{rll} g(t) &=& 50 \\[5pt] -0,88t + 145,4 &=& 50 & \\[5pt] \end{array}$

Mit dem solve-Befehl des CAS folgt $t \approx 108,4.$

Etwa ab dem 109. Tag nach Beginn der Behandlung, also 39 Tage nach Entfernung des Pflasters, ist eine Beschreibung durch die Gerade $g$ nicht mehr sinnvoll.

Gesucht ist der Zeitpunkt, an dem gilt:

$\begin{array}[t]{rll} h(t) & = & 100 \\[5pt] 8\cdot t\cdot \mathrm e^{-0,04\cdot t} +50 & = & 100 \\[5pt] \end{array}$

Mit dem solve-Befehl des CAS folgen die Zeitpunkte $t_1\approx 8,9$ und $t_2 \approx 53,8.$

Der Abbildung aus der Aufgabenstellung kann entnommen werden, dass der Hormonspiegel im Intervall $[t_1;t_2]$ über 100 liegt.

Nach ca. 9 Tagen sollte das Hormonpflaster also entfernt werden. Andernfalls hätte ein solcher Patient $53,8-8,9 \approx 45$ Tage lang einen Hormonspiegel von 100 oder mehr.

Wert angeben und beurteilen

$\begin{array}[t]{rll} h(10) &=& 8\cdot 10 \cdot \mathrm e^{-0,04\cdot 10} +50 \\[5pt] &\approx& 103,6 \end{array}$

Am 10. Tag beträgt der Wert des Hormonspiegels ca. 103,6 Prozentpunkte. Das liegt mit ca. 3,6 Prozentpunkten nur leicht über dem Sollwert von 100 und ist daher vermutlich relativ unbedenklich.

Bedingungsgleichungen begründen

Die Funktion $f$ soll durch eine Gleichung der Form $f(t)= a\cdot \mathrm e^{b\cdot t}$ beschrieben werden.

Zu dem Zeitpunkt, zu dem das Pflaster entfernt wird, muss die Funktion $f$ an die Funktion $h$ anschließen. Es muss also $f(10) = h(10)$ sein. Da $h(10) \approx 104$ und $f(10)= a\cdot \mathrm e^{10b}$ ist, entsteht so die Gleichung $\text{I}.$

Es ist angegeben, dass der Hormonspiegel gemäß der Funktion $f$ bereits am $30.$ Tag den Wert $h(70)$ erreicht:

$\begin{array}[t]{rll} h(70)&=& 8\cdot 70 \cdot \mathrm e^{-0,04\cdot 70} +50&\\[5pt] &\approx& 84 \end{array}$

Es muss also gelten $f(30)= h(70),$ wobei $f(30)= a\cdot \mathrm e^{30b}$ und $h(70)\approx 84$ ist. Daraus entsteht also die Bedingungsgleichung $\text{II}.$

Parameterwerte berechnen

Es ist folgendes Gleichungssystem gegeben:

$\begin{array}{lrll} \text{I:}\quad& a\cdot \mathrm e^{10b} &=& 104 \\ \text{II:}\quad& a\cdot \mathrm e^{30b} &=& 84 \\ \end{array}$

Durch Umformen der ersten Gleichung nach $a$ folgt:

$\begin{array}[t]{rll} \text{I:}\quad a\cdot \mathrm e^{10b} &=& 104 &\quad \scriptsize \mid\; :\mathrm e^{10b} \\[5pt] a &=& \dfrac{104}{\mathrm e^{10b}} \\[5pt] \end{array}$

Einsetzen in Gleichung $\text{II}$ liefert nun:

$b \approx -0,01$

Rechnung anzeigen

Für $a$ ergibt sich mit dem CAS also:

$\begin{array}[t]{rll} a &=& \dfrac{104}{\mathrm e^{10b}} &\quad \scriptsize \mid\;b=-0,0107 \\[5pt] &=& \dfrac{104}{\mathrm e^{10\cdot (-0,0107)}} \\[5pt] &\approx& 115,7 \end{array}$

Eine Gleichung der Funktion $f$ lautet somit:

$f(t) \approx 115,7 \cdot \mathrm e^{-0,0107t}$

Es soll gelten:

Rechenweg anzeigen

$h_k(70) \geq 100$

Ab $k\approx 11,7$ erreicht der Hormonspiegel am 70. Tag noch mindestens den Wert 100.

Der einzige Unterschied der beiden Funktionsterme ist der Faktor $k.$ Es gilt $h(t) = h_8(t).$

Ein Vergrößerung dieses Faktors führt zu einer Streckung des Graphen entlang der $y$ -Achse.

Je größer der Faktor $k$ ist, desto größer können generell auch die Funktionswerte werden. Es ergeben sich beispielsweise folgende Punkte:

Es gilt $h(0) = 50$ und auch $h_k(0) = 50$ unabhängig von $k.$ Die Graphen von $h$ und $h_k$ verlaufen also durch den Punkt $P(0\mid 50).$
Da $k\gt 8$ vorgegeben ist, nimmt $h_k$ für $t\gt 0$ größere Funktionswerte als $h$ an. Für $t\gt 0$ verläuft der Graph von $h_k$ also oberhalb des Graphen von $h.$
Durch den positiven Faktor $k$ wird die Anzahl und die Art der Extrempunkte nicht verändert. Der Graph von $h$ und der Graph von $h_k$ besitzen also die gleiche Anzahl und Art von Extrempunkten.
Beide Graphen besitzen eine waagerechte Asymptote mit der Gleichung $y=50.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?