Analysis 2
a)
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  Abbildung 1 zeigt den Graphen von
Abbildung 1 zeigt den Graphen von  sowie den Punkt
sowie den Punkt 
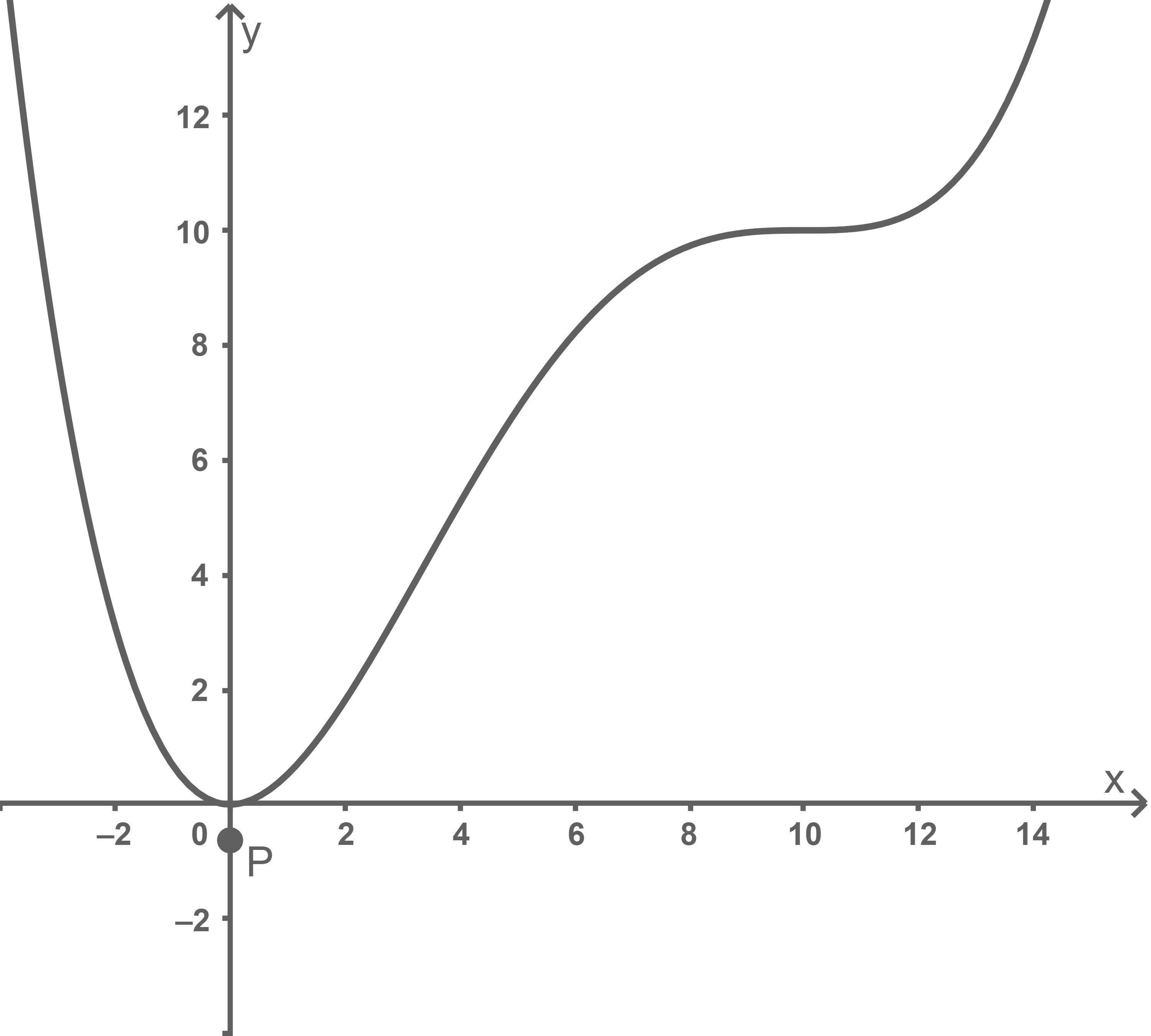
 und
und  wird mit
wird mit  bezeichnet.
bezeichnet.

Abb. 1
(1)
Der Graph von  besitzt den Tiefpunkt
besitzt den Tiefpunkt  Zeige rechnerisch, dass der Graph von
Zeige rechnerisch, dass der Graph von  keine weiteren Extrempunkte besitzt.
keine weiteren Extrempunkte besitzt.
Die Gerade durch die Punkte
(2)
Ermittle eine Gleichung von  und weise rechnerisch nach, dass
und weise rechnerisch nach, dass  die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt  ist.
ist.
(zur Kontrolle:  )
)
(3)
Der Graph von  und die Tangente
und die Tangente  schließen eine Fläche ein, die aus zwei Flächenstücken besteht.
Berechne den Inhalt dieser Fläche.
schließen eine Fläche ein, die aus zwei Flächenstücken besteht.
Berechne den Inhalt dieser Fläche.
(4)
Skizziere in Abbildung 1 zwei von  verschiedene Tangenten an den Graphen von
verschiedene Tangenten an den Graphen von  die die
die die  -Achse im Punkt
-Achse im Punkt  schneiden und deren Steigungen unterschiedliche Vorzeichen haben.
schneiden und deren Steigungen unterschiedliche Vorzeichen haben.
(5)
Der Graph der in  definierten Funktion
definierten Funktion  entsteht durch Transformationen aus dem Graphen von
entsteht durch Transformationen aus dem Graphen von  Der Punkt
Der Punkt  des Graphen von
des Graphen von  entsteht dabei aus dem Punkt
entsteht dabei aus dem Punkt  des Graphen von
des Graphen von  und für alle
und für alle  gilt
gilt
 mit
mit  Gib in diesem Zusammenhang die Bedeutung von
Gib in diesem Zusammenhang die Bedeutung von  und
und  an und berechne die Werte von
an und berechne die Werte von  und
und 
(3 + 4 + 5 + 3 + 4 Punkte)
b)
Zwei Radfahrer starten gleichzeitig nebeneinander auf einer geradlinigen Bahn aus einer Ruheposition. Radfahrer  beschleunigt 10 Sekunden lang und fährt danach mit konstanter Geschwindigkeit weiter. Radfahrer
beschleunigt 10 Sekunden lang und fährt danach mit konstanter Geschwindigkeit weiter. Radfahrer  beschleunigt 12 Sekunden lang und fährt dann mit konstanter Geschwindigkeit weiter.
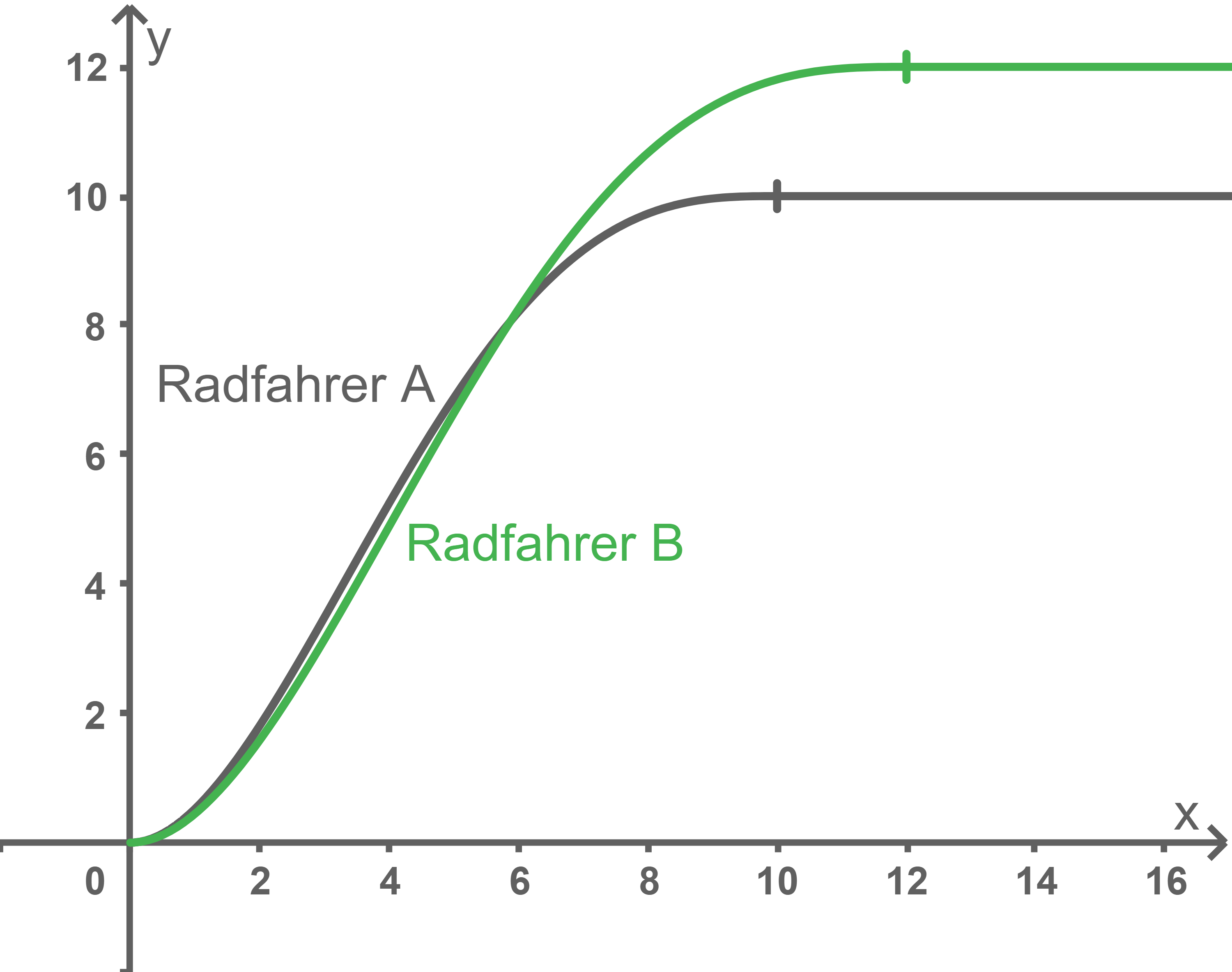
Abbildung 2 stellt die Geschwindigkeitsverläufe der beiden Radfahrer in den ersten 15 Sekunden nach dem Start dar. Dabei wird der Geschwindigkeitsverlauf von Radfahrer
beschleunigt 12 Sekunden lang und fährt dann mit konstanter Geschwindigkeit weiter.
Abbildung 2 stellt die Geschwindigkeitsverläufe der beiden Radfahrer in den ersten 15 Sekunden nach dem Start dar. Dabei wird der Geschwindigkeitsverlauf von Radfahrer  in den ersten 10 Sekunden nach dem Start durch die Funktion
in den ersten 10 Sekunden nach dem Start durch die Funktion  aus Aufgabe a) beschrieben.
Der Geschwindigkeitsverlauf von Radfahrer
aus Aufgabe a) beschrieben.
Der Geschwindigkeitsverlauf von Radfahrer  wird in den ersten 12 Sekunden nach dem Start durch die in
wird in den ersten 12 Sekunden nach dem Start durch die in  definierte Funktion
definierte Funktion  mit
mit
 beschrieben. Dabei ist
beschrieben. Dabei ist  die seit dem Start vergangene Zeit in Sekunden und
die seit dem Start vergangene Zeit in Sekunden und  bzw.
bzw.  die Geschwindigkeit in Meter pro Sekunde.
die Geschwindigkeit in Meter pro Sekunde.
 bezeichnet.
bezeichnet.

Abb. 2
(1)
Berechne die Geschwindigkeit von Radfahrer  drei Sekunden nach dem Start sowie den Zeitpunkt, zu dem er eine Geschwindigkeit von 8 Meter pro Sekunde erreicht.
drei Sekunden nach dem Start sowie den Zeitpunkt, zu dem er eine Geschwindigkeit von 8 Meter pro Sekunde erreicht.
(2)
Ermittle die konstante Geschwindigkeit, mit der sich Radfahrer  ab dem Zeitpunkt 12 Sekunden nach dem Start bewegt.
Zeige durch Rechnung, dass der zum Radfahrer
ab dem Zeitpunkt 12 Sekunden nach dem Start bewegt.
Zeige durch Rechnung, dass der zum Radfahrer  gehörende Graph in Abbildung 2 an der Stelle 12 keinen Knick aufweist.
gehörende Graph in Abbildung 2 an der Stelle 12 keinen Knick aufweist.
Nach dem Start gibt es genau einen Zeitpunkt, zu dem die Geschwindigkeiten beider Radfahrer gleich groß sind. Im Modell wird dieser Zeitpunkt mit
(3)
Bestimme rechnerisch 
(4)
Im Folgenden ist ein Lösungsweg für eine Aufgabe im gegebenen Sachzusammenhang dargestellt.



 hat für
hat für  nur die Lösung
nur die Lösung  mit
mit 



 Gib die Bedeutung von
Gib die Bedeutung von  für
für  im Sachzusammenhang an und interpretiere das Ergebnis
im Sachzusammenhang an und interpretiere das Ergebnis 
(5)
(i)
Zeige, dass Radfahrer  in den ersten
in den ersten  Sekunden ungefähr
Sekunden ungefähr  Meter zurücklegt.
Meter zurücklegt.
(ii)
Bestimme rechnerisch den Zeitpunkt, zu dem Radfahrer 
 Meter vom Start entfernt ist.
Meter vom Start entfernt ist.
(3 + 3 + 2 + 4 + 4 Punkte)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
(1)
Für die erste Ableitung von  liefert das CAS:
liefert das CAS:
 Die notwendinge Bedingung für Extremstellen
Die notwendinge Bedingung für Extremstellen  liefert mit dem solve-Befehl des CAS:
liefert mit dem solve-Befehl des CAS:
![\(\begin{array}[t]{rll}
x_1&=&0 \\[5pt]
x_2&=&10
\end{array}\)](https://mathjax.schullv.de/491f2306712c54f96ac39904613d28b1b69bd16e700d6c99e1ba750f49faedaf?color=5a5a5a) Einsetzen von Werten um
Einsetzen von Werten um  herum in
herum in  liefert weiter, dass sich das Vorzeichen an dieser Stelle nicht ändert. Somit besitzt der Graph von
liefert weiter, dass sich das Vorzeichen an dieser Stelle nicht ändert. Somit besitzt der Graph von  dort keinen Extrempunkt, das heißt nach der notwendingen Bedingung für Extremstellen ist
dort keinen Extrempunkt, das heißt nach der notwendingen Bedingung für Extremstellen ist  die einzige Extremstelle.
die einzige Extremstelle.
(2)
Gleichung von  ermitteln
Die gesuchte Gerade
ermitteln
Die gesuchte Gerade  besitzt die allgemeine Gleichung
besitzt die allgemeine Gleichung  wobei der
wobei der  -Achsenabschnitt
-Achsenabschnitt  als
als  gegeben ist, da
gegeben ist, da  durch
durch  verläuft. Einsetzen der Koordinaten von
verläuft. Einsetzen der Koordinaten von  und Auflösen nach der Steigung
und Auflösen nach der Steigung  im CAS liefert:
im CAS liefert:
 Eine Gleichung von
Eine Gleichung von  ist somit durch
ist somit durch  gegeben.
Tangente rechnerisch nachweisen
Es gilt
gegeben.
Tangente rechnerisch nachweisen
Es gilt  Einsetzen von
Einsetzen von  in
in  und
und  liefert:
liefert:
![\(\begin{array}[t]{rll}
f(5)&=&\dfrac{3}{1000} \cdot 5^4-\dfrac{8}{100} \cdot 5^3+\dfrac{6}{10} \cdot 5^2 \\[5pt]
&=&\dfrac{55}{8} \\[5pt]
&=&t(5) \\[10pt]
f](https://mathjax.schullv.de/8be1926f2e4b06c14526892bd587ba6aaa754d8057221e0b36bf68cacbc06d72?color=5a5a5a) Somit ist
Somit ist  die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt mit den Koordinaten
im Punkt mit den Koordinaten 
(3)
Gleichsetzen von  und
und  liefert
liefert  Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
x_1&=&\dfrac{25-5 \sqrt{22}}{3} \\[5pt]
x_2&=&5 \\[5pt]
x_3&=&\dfrac{25+5 \sqrt{22}}{3}
\end{array}\)](https://mathjax.schullv.de/1a768e322a7b6295da83a402f19cfecda65ac53656735457d4e9f87e12aa2ae9?color=5a5a5a) Da
Da  die Tangente an den Graphen von
die Tangente an den Graphen von  im Punkt
im Punkt  ist, berührt sie diesen an der Stelle
ist, berührt sie diesen an der Stelle  nur. Da zudem
nur. Da zudem  gilt und
gilt und  in diesem Bereich über dem Graphen von
in diesem Bereich über dem Graphen von  verläuft, folgt, dass
verläuft, folgt, dass  zwischen
zwischen  und
und  über dem Graphen von
über dem Graphen von  liegt. Somit ergibt sich für den gesuchten Flächeninhalt mit dem CAS:
liegt. Somit ergibt sich für den gesuchten Flächeninhalt mit dem CAS:

![\( =\dfrac{770}{81}
\sqrt{22}\approx 44,59\;[\text{FE}]\)](https://mathjax.schullv.de/ba7d4804beee51d43ff2615b417a4f8818438b95c4de1ef1d70e08955a7ef041?color=5a5a5a)
(4)
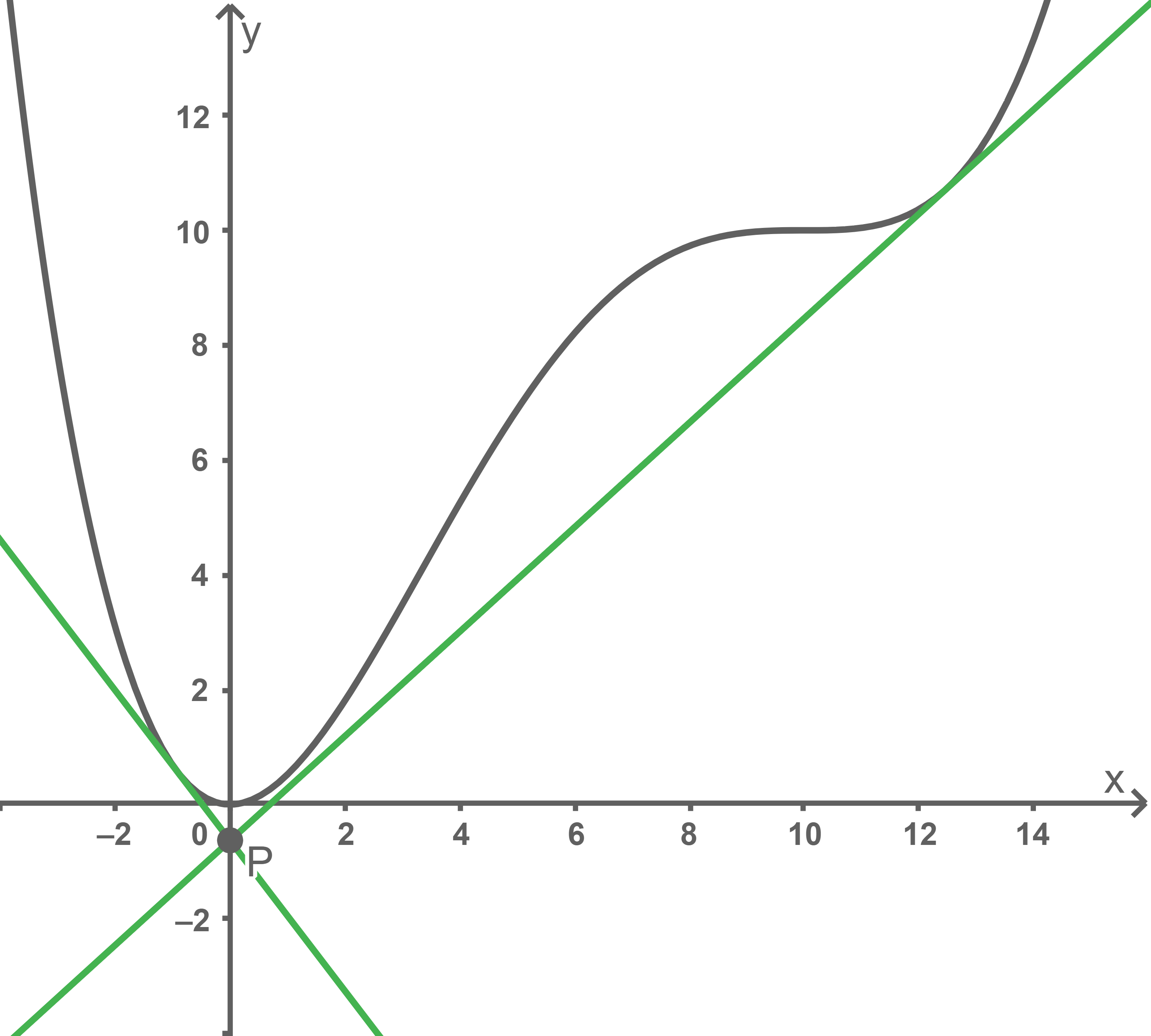
(5)
Der Graph von  entsteht aus dem Graphen von
entsteht aus dem Graphen von  indem mit dem Faktor
indem mit dem Faktor  in
in  -Richtung gestreckt wird und mit dem Faktor
-Richtung gestreckt wird und mit dem Faktor  in
in  -Richtung gestreckt wird. Für
-Richtung gestreckt wird. Für  folgt somit:
folgt somit:
![\(\begin{array}[t]{rll}
g(12)&=&a\cdot f(10) \\[5pt]
12&=&a\cdot 10 &\quad \scriptsize \mid\;:10\\[5pt]
\dfrac{6}{5}&=&a
\end{array}\)](https://mathjax.schullv.de/81a52b7a4b89230ed92c1a25bbc932dd61cbe92f2a05431121028243e6c30251?color=5a5a5a) Für den Wert von
Für den Wert von  ergibt sich:
ergibt sich:
![\(\begin{array}[t]{rll}
12&=&\dfrac{1}{b}\cdot10 &\quad \scriptsize \mid\;\cdot b \\[5pt]
12b&=&10 &\quad \scriptsize \mid\;:12\\[5pt]
b&=&\dfrac{5}{6}
\end{array}\)](https://mathjax.schullv.de/5e1311930daf62c9460d12d43860eae2201e6abb5287b3908af606bf5dfc5a04?color=5a5a5a)
b)
(1)
(2)
Konstante Geschwindigkeit ermitteln
Die gesuchte konstante Geschwindigkeit von Radfahrer  beträgt somit
beträgt somit  Knickfreiheit zeigen
Für die Ableitung von
Knickfreiheit zeigen
Für die Ableitung von  folgt mit dem CAS:
folgt mit dem CAS:
 Für
Für  folgt somit:
folgt somit:
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/31889edcb3f99252ce035b9ef96787e006f41519de2b7ba72ea86a850786468e?color=5a5a5a) Da Radfahrer
Da Radfahrer  sich ab 12 Sekunden nach dem Start mit konstanter Geschwindigkeit fortbewegt, weist der zugehörige Graph in Abbildung 2 somit an der Stelle
sich ab 12 Sekunden nach dem Start mit konstanter Geschwindigkeit fortbewegt, weist der zugehörige Graph in Abbildung 2 somit an der Stelle  keinen Knick auf.
keinen Knick auf.
(3)
Aus der Gleichung  folgt mit dem solve-Befehl des CAS als Lösung im Zeitraum
folgt mit dem solve-Befehl des CAS als Lösung im Zeitraum 

(4)
Bedeutung von  angeben
Der Funktionswert
angeben
Der Funktionswert  gibt an, um wie viele Meter pro Sekunde Radfahrer
gibt an, um wie viele Meter pro Sekunde Radfahrer  zum Zeitpunkt von
zum Zeitpunkt von  Sekunden nach dem Start schneller ist als Radfahrer
Sekunden nach dem Start schneller ist als Radfahrer  Interpretation des Ergebnisses
Der größte Unterschied der Geschwindigkeiten der beiden Radfahrer innerhalb der ersten
Interpretation des Ergebnisses
Der größte Unterschied der Geschwindigkeiten der beiden Radfahrer innerhalb der ersten  Sekunden nach dem Start beträgt ca.
Sekunden nach dem Start beträgt ca. 
(5)
(i)
(ii)
Mit dem solve-Befehl des CAS folgt  Somit ist Radfahrer
Somit ist Radfahrer  nach ca.
nach ca.  Sekunden
Sekunden  Meter vom Start entfernt.
Meter vom Start entfernt.