A2

Gegeben sind die Funktionen $f$ und $g$ mit

$f(x)=x^3-6\cdot x^2+3\cdot x +10 , x \in \mathbb{R},$

und

$g(x)=-6 \cdot x+10, x \in \mathbb{R}.$

(1)

Berechne die Stellen, an denen die Graphen von $f$ und $g$ gemeinsame Punkte besitzen.

(2)

Der Punkt $P(3 \mid f(3))$ ist einer dieser gemeinsamen Punkte.

Zeige: Der Graph von $g$ ist die Tangente an den Graphen von $f$ im Punkt $P.$

(3 + 2 Punkte)

Die Funktion $f$ ist gegeben durch die Gleichung

$f(x)=3 \cdot x^2-12, x \in \mathbb{R}.$

(i)

Berechne die Nullstellen von $f.$

(ii)

Berechne den Inhalt der Fläche, die vom Graphen von $f$ und der $x$ -Achse eingeschlossen wird.

(5 Punkte)

Die Funktion $f$ ist gegeben durch die Gleichung

$f(x)=x^2 \cdot \mathrm e ^x, x \in \mathbb{R}.$

(1)

Zeige: $f^{\prime}(x)=x \cdot(x+2) \cdot \mathrm e ^x.$

(2)

Bestimme (z. B. unter Verwendung des Vorzeichenwechselkriteriums) die Extremstellen und die Art der Extremstellen der Funktion $f.$

(2 + 3 Punkte)

(1)

Die Histogramme I bis III in den Abbildungen 1-1 bis 1-3 zeigen Wahrscheinlichkeitsverteilungen von drei binomialverteilten Zufallsgrößen $A, B$ und $C.$ Es gilt jeweils $n=10.$ Zu jeder Zufallsgröße gehört eine der Wahrscheinlichkeiten $p_1=0,2$ , $p_2=0,4$ und $p_3=0,8.$

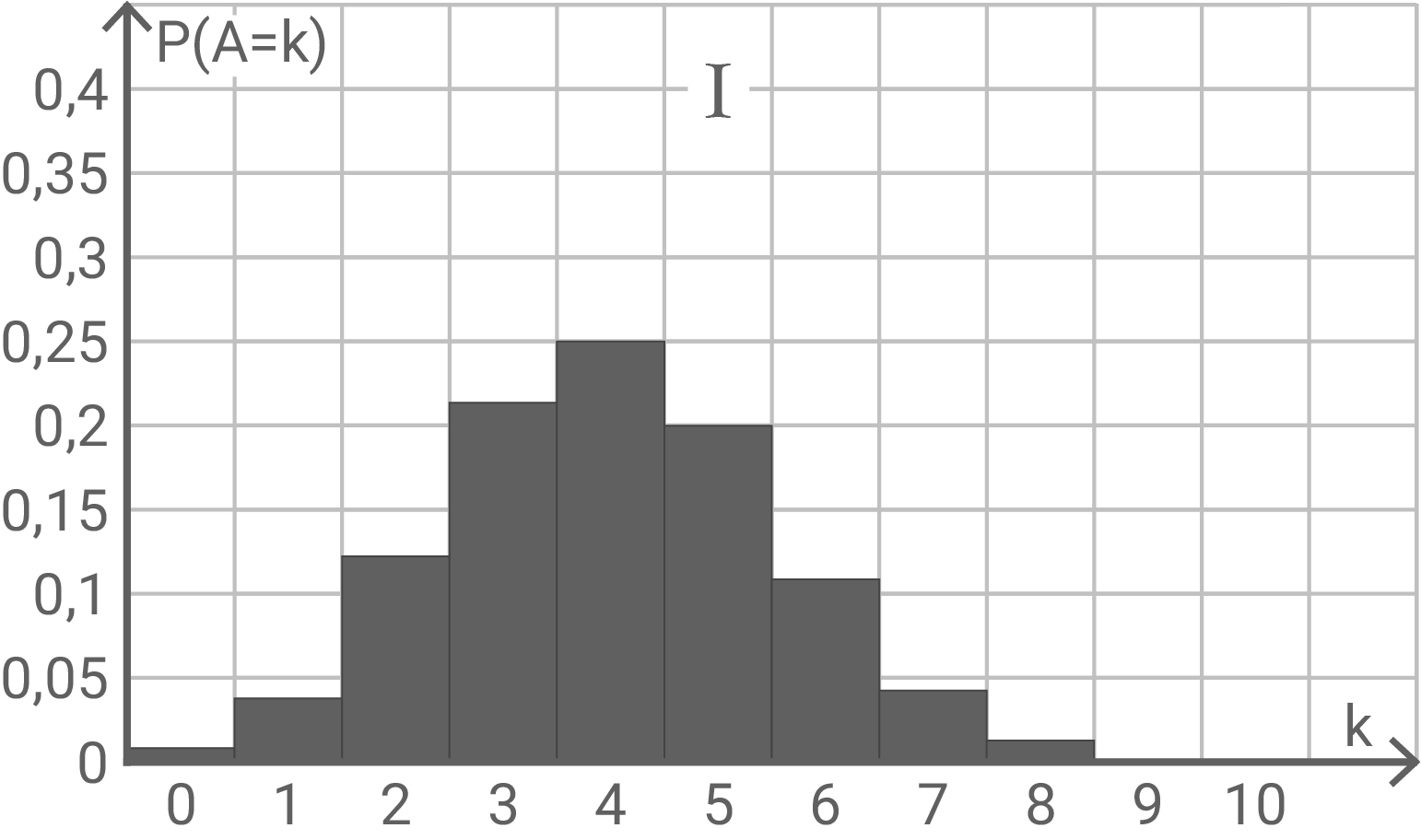
Abbildung 1-1

Abbildung 1-2

Abbildung 1-3

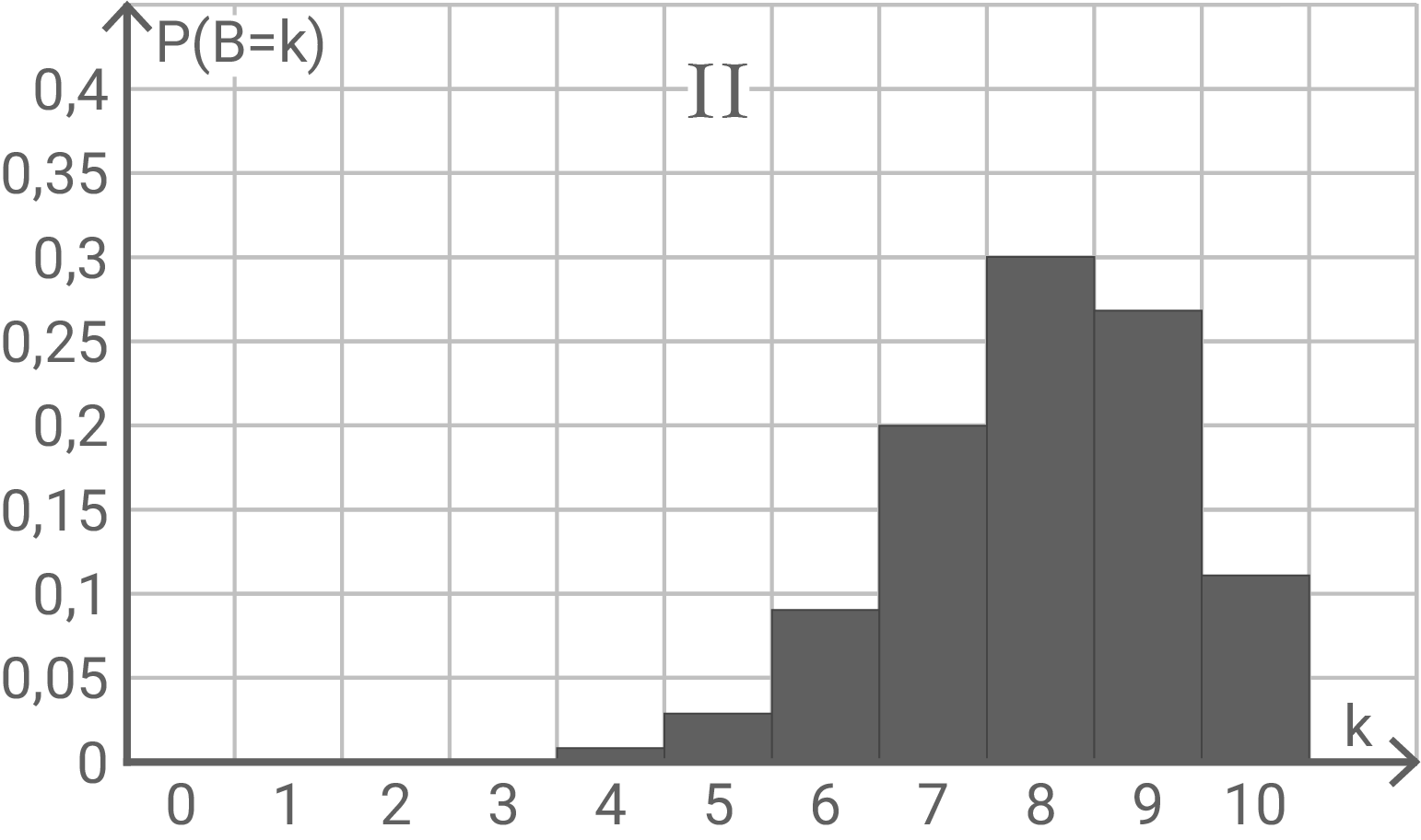
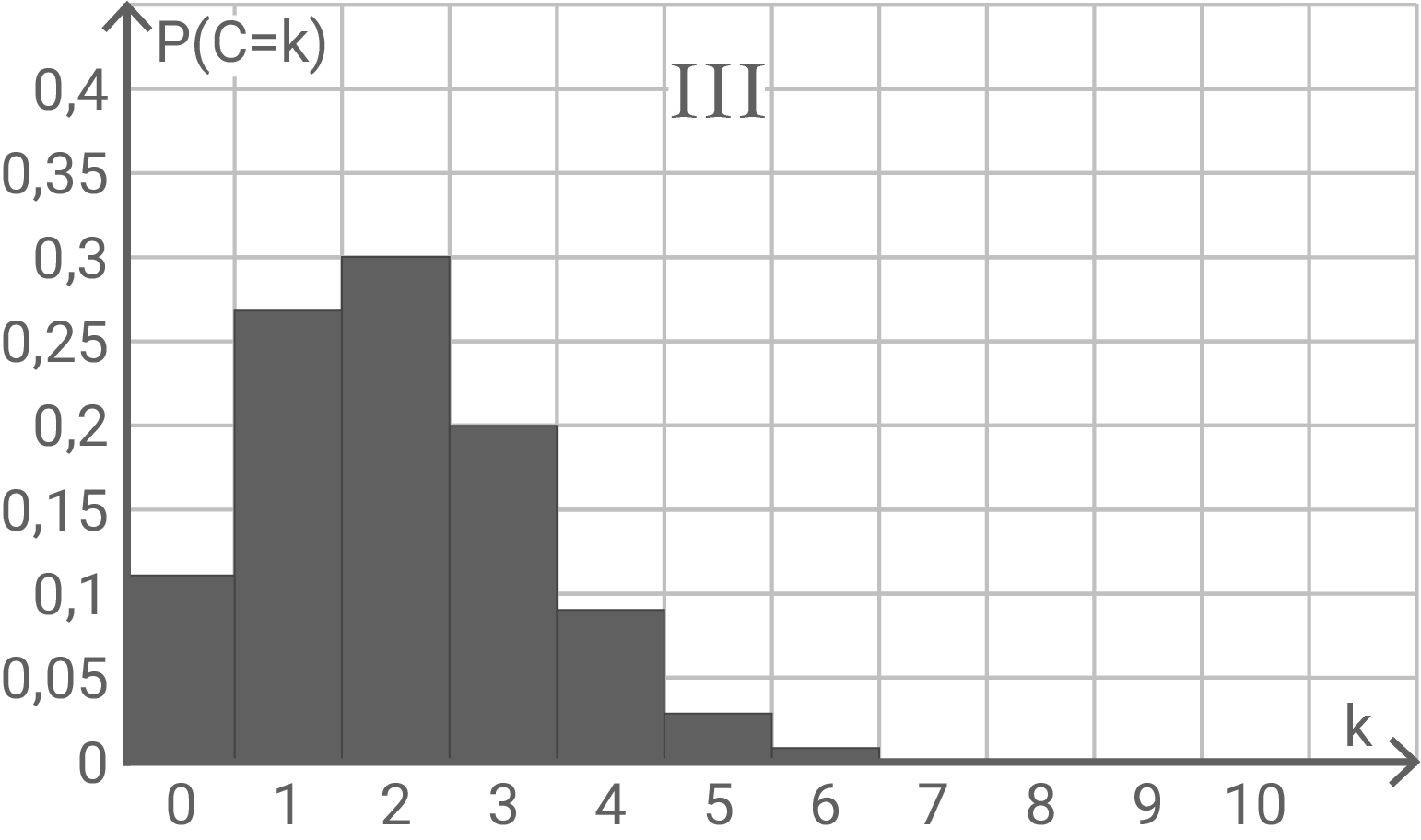
Ordne den Histogrammen I bis III die jeweils passende Wahrscheinlichkeit zu.

(2)

Eine weitere Zufallsgröße $X$ ist binomialverteilt mit $n=10.$

Das unvollständige Histogramm der Verteilung ist in Abbildung 2 dargestellt.

Es gilt: $P(X \geq 4) \approx 0,35.$

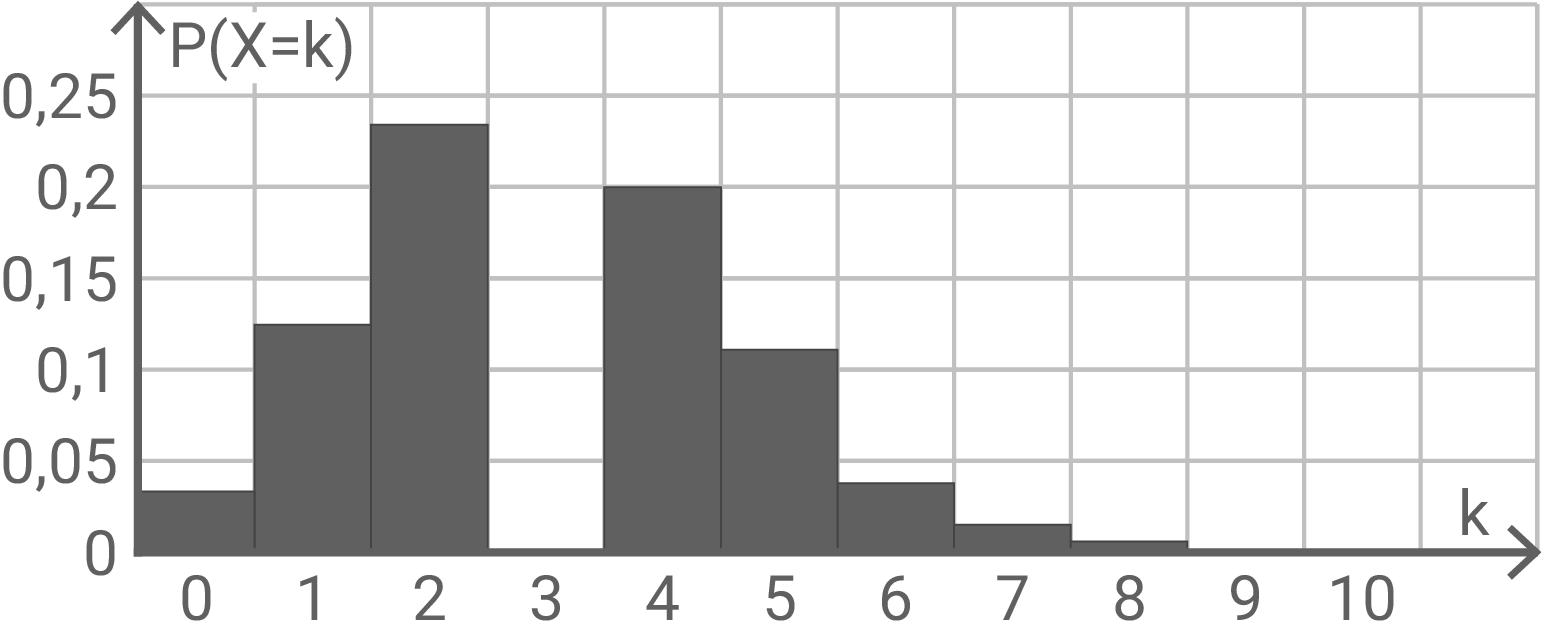
Abbildung 2

(i)

Ermittle näherungsweise die Wahrscheinlichkeit $P(X \leq 2).$

(ii)

Ermittle näherungsweise die Wahrscheinlichkeit $P(X =3).$

(2 + 3 Punkte)

(1)

Die Zufallsgröße $X$ ist binomialverteilt mit den Parametern $n$ und $p=0,2$ . Für die Standardabweichung $\sigma$ von $X$ gilt: $\sigma=1,2.$

Berechne $n.$

(2)

In einer Urne befinden sich 2 schwarze und 8 weiße Kugeln. Aus der Urne wird mit Zurücklegen neunmal eine Kugel gezogen.

(i)

Gib einen Term für die Wahrscheinlichkeit an, dass dabei genau zweimal eine schwarze Kugel gezogen wird.

(ii)

Beschreiben Sie ein Ereignis im Sachkontext der Aufgabe mit einer Wahrscheinlichkeit von $0,2^2 \cdot\left(\begin{array}{l}7 \\ 3\end{array}\right) \cdot 0,2^3 \cdot 0,8^4.$

(2 + 3 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

(1)

Gleichsetzen:

Rechenweg anzeigen

$x(x^2-6x+9)= 0$

Mit dem Satz vom Nullprodukt folgt, dass $x=0$ oder $x^2-6 \cdot x+9=0$ sein muss. Es ist also $x_1=0$ und weiterhin folgt mit der $pq$ -Formel:

$\begin{array}[t]{rll} x_{2,3}&=&-\dfrac{-6}{2} \pm \sqrt{\left(\dfrac{-6}{2}\right)^2-9} \\[5pt] &=& 3 \pm \sqrt{3^2-9} \\[5pt] &=& 3 \end{array}$

An den Stellen $x_1=0$ und $x_2=3$ besitzen der Graph von $f$ und der Graph von $g$ gemeinsame Punkte.

(2)

Die Steigung des Graphen von $f$ an der Stelle $x=3$ lässt sich mit Hilfe der ersten Ableitungsfunktion von $f$ bestimmen:

$\(\begin{array}[t]{rll} f$

Dies entspricht der Steigung von $g.$ Es gilt also $\(f$

Der Graph von $g$ ist eine Gerade. Im gemeinsamen Punkt $P$ haben diese Gerade und der Graph von $f$ die gleiche Steigung. Daher ist der Graph von $g$ die Tangente an den Graphen von $f$ im Punkt $P.$

(i)

$\begin{array}[t]{rll} f(x)&=& 0 \\[5pt] 3x^2-12&=& 0&\quad \scriptsize \mid\; :3\\[5pt] x^2-4&=& 0&\quad \scriptsize \mid\;+4 \\[5pt] x^2&=& 4 &\quad \scriptsize \mid\; \sqrt{\;} \\[5pt] x&=&\pm \sqrt{4} \end{array}$

Die Nullstellen von $f$ folgen mit $x_1=-2$ und $x_2=2.$

(ii)

Der Inhalt der Fläche, die vom Graphen von $f$ und der $x$ -Achse eingeschlossen wird, wird mit dem Betragswert des folgenden Integrals bestimmt:

Rechenweg anzeigen

$\displaystyle\int_{-2}^2 f(x)\; \mathrm d x =...$

Der Inhalt der Fläche, die vom Graphen von $f$ und der $x$ -Achse eingeschlossen wird, beträgt $32 \;\text{FE}.$

(1)

Produktregel anwenden:

$\(\begin{array}[t]{rll} f$

(2)

Lösungsweg unter Verwendung des Vorzeichenwechselkriteriums

1. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

Da stets $\mathrm e^x \neq 0$ gilt, folgt mit dem Satz vom Nullprodukt $x=0$ oder $2 +x=0.$

Daraus folgen $x_{E_1}=-2$ und $x_{E_2}= 0$ als mögliche Extremstellen.

2. Schritt: Vorzeichenwechselkriterium anwenden

Es gilt:

$f^{\prime}(-3)$ $= (-3)\cdot (2 -3)\cdot \mathrm e^{-3}$ $=3 \cdot \mathrm e ^{-3} \gt0$

$f^{\prime}(-1)$ $= (-1)\cdot (2 -1)\cdot \mathrm e^{-1}$ $=- \mathrm e ^{-1}\lt0$

$f^{\prime}(1)$ $= (2 +1)\cdot \mathrm e^{1}$ $=3 \cdot \mathrm e \gt0$

Somit liegt an der Stelle $x_{E_1}=-2$ ein Vorzeichenwechsel von positiven zu negativen Funktionswerten von $f^{\prime}$ vor. $x_{E_1}=-2$ ist also eine lokale Maximalstelle von $f.$

An der Stelle $x_{E_2}=0$ liegt ein Vorzeichenwechsel von negativen zu positiven Funktionswerten von $f^{\prime}$ vor. $x_{E_2}=0$ ist also eine lokale Minimalstelle von $f.$

Alternativer Lösungsweg unter Verwendung der hinreichenden Bedingung für Extremstellen

1. Schritt: Zweite Ableitung bilden

Produktregel anwenden:

$\(\begin{array}[t]{rll} f$

2. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

Da stets $\mathrm e^x \neq 0$ gilt, folgt mit dem Satz vom Nullprodukt $x=0$ oder $2 +x=0.$

Daraus folgen $x_{E_1}=-2$ und $x_{E_2}= 0$ als mögliche Extremstellen.

3. Schritt: Hinreichende Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

$x_{E_1}=-2$ ist also eine lokale Maximalstelle von $f.$

$\(\begin{array}[t]{rll} f$

$x_{E_2}=0$ ist also eine lokale Minimalstelle von $f.$

(1)

Zuordnung:

$\text{I} \rightarrow p_2$

$\text{II} \rightarrow p_3$

$\text{III} \rightarrow p$

(2)

(i)

$P(X \leq 2)$ $=P(X=0)+P(X=1)+P(X=2)$

Aus dem Histogramm können die passenden Werte abgelesen werden, also folgt:

$\begin{array}[t]{rll} P(X \leq 2)&\approx& 0,03+0,12+0,23 \\[5pt] &=&0,38 \end{array}$

(ii)

$P(X=3)$ $=1-P(X \leq 2)-P(X \geq 4)$

$\begin{array}[t]{rll} P(X =3)&\approx& 1-0,38-0,35 \\[5pt] &=&0,27 \end{array}$

(1)

$\begin{array}[t]{rll} \sigma&=& 1,2 \\[5pt] \sqrt{n \cdot p \cdot(1-p)}&=&1,2 \\[5pt] \sqrt{n \cdot 0,2 \cdot 0,8}&=& 1,2&\quad \scriptsize \mid\;(\;)^2 \\[5pt] 0,16\cdot n&=& 1,44 &\quad \scriptsize \mid\;:0,16 \\[5pt] n&=& 9 \end{array}$

(2)

(i)

$\left(\begin{array}{l}9 \\ 2\end{array}\right) \cdot 0,2^2 \cdot 0,8^7$

(ii)

Beispiel: Von den neun gezogenen Kugeln sind die ersten beiden schwarz. Von den weiteren sieben gezogenen Kugeln sind genau drei schwarz.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?