Wahlpflichtteil

Aufgabe 1 - Analysis

Gegeben sind die in $\mathbb{R}$ definierten ganzrationalen Funktionen $f_k$ mit $f_k(x)=x^4+(2-k)\cdot x^3-k\cdot x^2$ und $k\in\mathbb{R}.$

Begründe, dass der Graph von $f_2$ symmetrisch bezüglich der $y$ -Achse ist.

Es gibt einen Wert von $k,$ für den die Stelle $x=1$ eine Wendestelle von $f_k$ ist.

Berechne diesen Wert von $k.$

(1 + 4 Punkte)

Aufgabe 2 - Analysis

Gegeben ist die Funktion $f$ mit $f(x)=(x^{2}-x)\cdot \mathrm e^{x}$ .

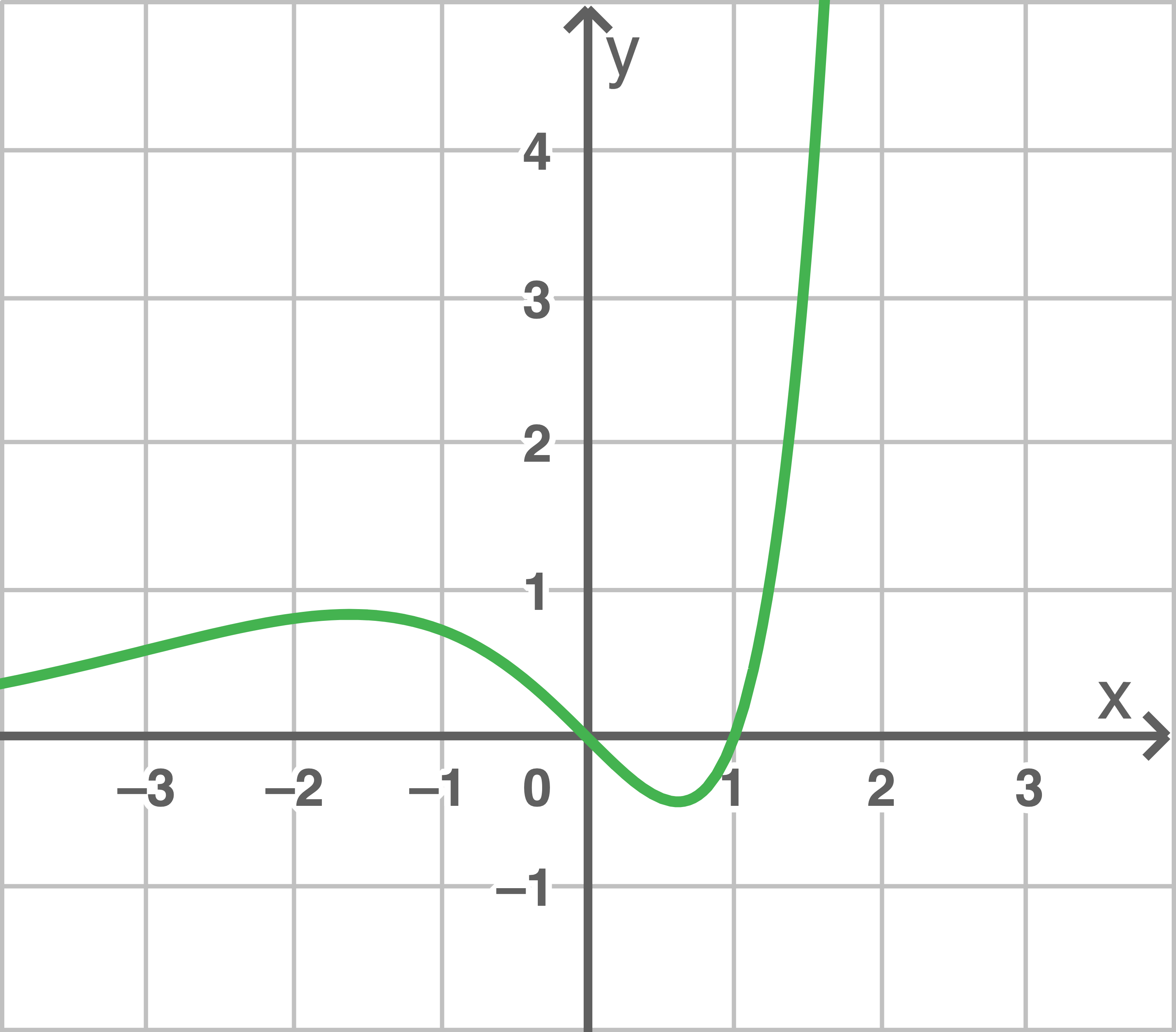
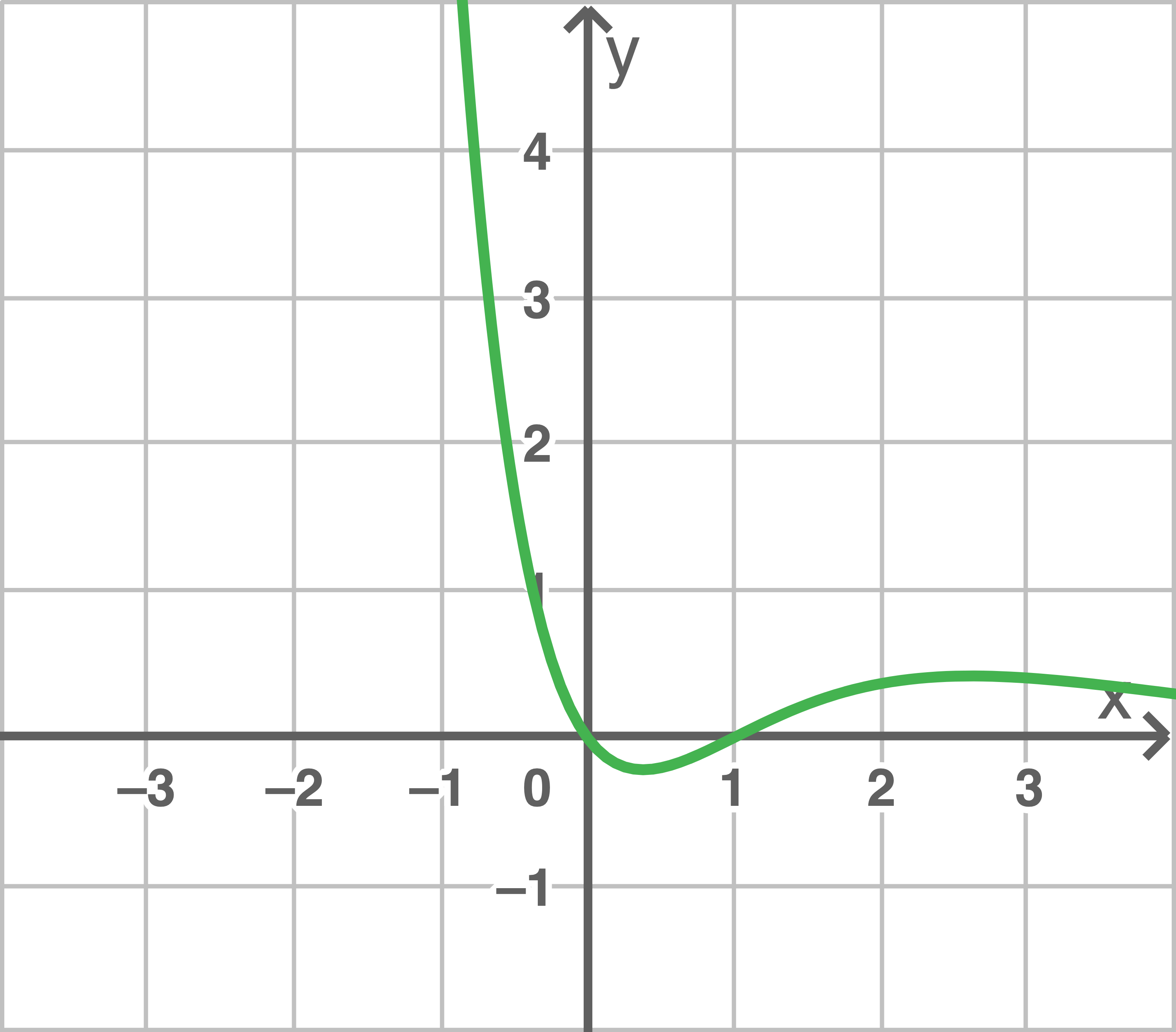
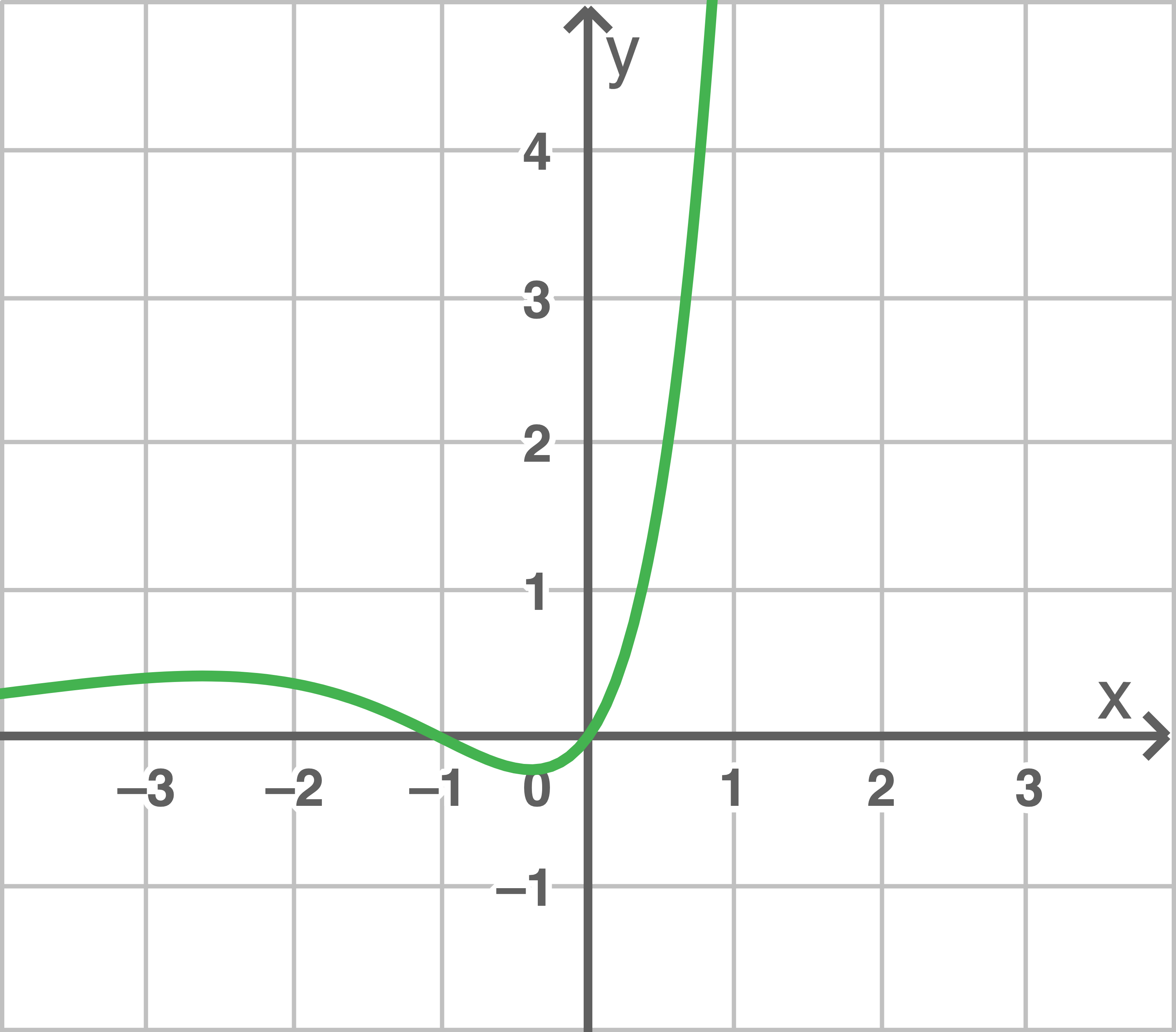
Entscheide, welcher der drei dargestellten Graphen zur Funktion $f$ gehört.

Graph (I)

Graph (II)

Graph (III)

Ermittle die Funktionsgleichung der Ableitungsfunktion $\(f$ .
Hinweis: Ein Vereinfachen des Funktionsterms ist nicht erforderlich.

(3 + 2 Punkte)

Aufgabe 3 - Vektorielle Geometrie

In einem mathematischen Modell wird im Punkt $A (1\mid -3\mid 0)$ senkrecht zum Erdboden ein $10$ Meter hoher Fahnenmast errichtet. Der Erdboden befindet sich in der $xy$ -Ebene, wobei eine Längeneinheit einem Meter entspricht. Die Koordinaten des Schattenpunktes $S$ der Mastspitze auf dem Boden zu einem bestimmten Zeitpunkt lauten $S (9\mid 3\mid 0)$ .

Berechne die Länge des Schattens des Fahnenmastes auf dem Boden.

Ermittle einen Vektor, der die Richtung der Sonnenstrahlen beschreibt.

Zu einem anderen Zeitpunkt ändert sich die $z$ -Koordinate des Sonnenstrahlvektors bei gleichbleibender $x$ - und $y$ -Koordinate so, dass der Schatten des Fahnenmastes auf dem Boden länger wird. Gib ein mögliches Beispiel für einen solchen Sonnenstrahlvektor an.

(2 + 2 + 1 Punkte)

Aufgabe 4 - Vektorielle Geometrie

Gegeben ist das Dreieck $ABC$ mit den Punkten $A(2|3|-4),$ $B(-1|1|0)$ und $C(2|1|-4).$

Zeige rechnerisch, dass das Dreieck im Punkt $C$ einen rechten Winkel hat.

Berechne den Flächeninhalt der Dreiecksfläche.

(3 + 2 Punkte)

Aufgabe 5 - Stochastik

$60\,\%$ der Kunden eines Reiseunternehmens reisen gerne in die Region A, $30\,\%$ in die Region B, $20\,\%$ reisen in jede der beiden Regionen gerne.

Unter denjenigen Kunden, die gerne in die Region A reisen, wird eine Person zufällig ausgewählt. Bestimme die Wahrscheinlichkeit dafür, dass diese Person auch gerne in die Region B reist.

Berechne den Anteil der Kunden, die entweder in die Region A oder in die Region B gerne reisen.

(2 + 3 Punkte)

Aufgabe 6 - Stochastik

Eine Urne enthält 3 rote und 5 gelbe Kugeln.

Es werden nacheinander zwei Kugeln ohne Zurücklegen gezogen.

Berechne die Wahrscheinlichkeit $p_{1}$ , dass die beiden Kugeln gelb sind.

Gib die Wahrscheinlichkeit $p_{2}$ dafür an, dass die zweite Kugel gelb ist, wenn die erste Kugel bereits gelb war.

Es werden nacheinander $5$ Kugeln mit Zurücklegen gezogen.

Erläutere im Sachzusammenhang, was mit dem folgenden Term berechnet wird. Gehe dabei auf die einzelnen Faktoren des Terms ein.

$\pmatrix{5\\2}\cdot \left(\dfrac{3}{8}\right)^2\cdot \left(\dfrac{5}{8}\right)^3$

(2 + 3 Punkte)

(10 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1 - Analysis

Für $k=2$ gilt:

$\begin{array}[t]{rll} f_2(x)&=& x^4+\underbrace{\left(2-2\right)\cdot x^3}_{=0}-k\cdot x^2&\\[5pt] &=&x^4-k\cdot x^2 \end{array}$

Der Funktionstermin von $f_2$ hat somit nur gerade Exponenten, also verläuft der Graph von $f_2$ symmetrisch zur $y$ -Achse.

$\(\begin{array}[t]{rll} f_k$

Für die Wendestelle $x=1$ gilt:

$\(\begin{array}[t]{rll} f_k$

Auf die Überprüfung des hinreichenden Kriteriums kann verzichtet werden, da laut Aufgabenstellung nur ein $k$ existiert, für das es eine Wendestelle gibt.

Lösung 2 - Analysis

Die Graphen unterscheiden sich in den Nullstellen.

$\begin{array}[t]{rll} f(x)&=& 0&\quad \scriptsize \\[5pt] (x^2 -x) \cdot \mathrm e^x&=& 0 & \\[5pt] x\cdot (x - 1)\cdot \mathrm e^x&=& 0 &\quad \scriptsize \\[5pt] \end{array}$

Da stets $\mathrm e^x\neq0$ gilt, folgt mit dem Satz vom Nullprodukt $x_1=0$ und $x-1=0.$

$\begin{array}[t]{rll} x-1&=& 0 &\quad \scriptsize\mid +1 \\[5pt] x_2&=&1 &\quad \scriptsize \\ \end{array}$

Die Nullstellen der Funktion sind folglich bei $x_1=0$ und $x_2=1$ .

Graph III kann ausgeschlossen werden, da die Nullstellen nicht übereinstimmen.

Wegen $\lim\limits_{x\to\infty} f(x) \neq \infty$ kann der Graph II ebenfalls ausgeschlossen werden.

Der Graph zu $f(x)$ ist somit der Graph I.

Mit der Produktregel folgt:

$\(\begin{array}[t]{rll} f(x)&=&(x^2 -x) \cdot \mathrm e^x & \\[5pt] f$

Lösung 3 - Vektorielle Geometrie

$\begin{array}[t]{rll} |\overrightarrow{AS}|&=&\left|\pmatrix{9-1\\3-(-3)\\0-0}\right| & \\[5pt] &=&\sqrt{8^2+6^2+0^2} & \\[5pt] &=&\sqrt{100} & \\[5pt] &=& 10 \; [\,\text{m}] \end{array}$

Der Schatten des Fahnenmasts auf dem Boden ist $10 \,\text{m}$ lang.

Koordinaten der Mastspitze $M$ bestimmen

Da der Mast $10 \,\text{m}$ hoch ist und senkrecht zur $xy$ -Ebene steht, folgt: $\overrightarrow{OM}=\pmatrix{1\\-3\\10}.$

Richtungsvektor $\overrightarrow{s}$ der Sonnenstrahlen ermitteln

$\begin{array}[t]{rll} \overrightarrow{s}&=&\overrightarrow{OS}-\overrightarrow{OM} & \\[5pt] &=&\pmatrix{9\\3\\0}- \pmatrix{1\\-3\\10}& \\[5pt] &=&\pmatrix{8\\6\\-10} \end{array}$

Je kleiner der Betrag der $z$ -Koordinate, desto flacher fallen die Sonnenstrahlen ein.

Damit der Schatten auf dem Boden länger wird, muss der Betrag der $z$ -Koordinate folglich kleiner werden.

Ein möglicher Vektor solch eines Sonnenstrahls ist somit beispielsweise $s_1=\pmatrix{8\\6\\-5}.$

Lösung 4 - Vektorielle Geometrie

Es gilt:

$\begin{array}[t]{rll} \overrightarrow{AC} \circ \overrightarrow{BC} &=& \pmatrix{2-2\\1-3\\-4 + 4} \circ \pmatrix{2+1\\1-1\\-4-0}&\\[5pt] &=& \pmatrix{0\\-2\\0} \circ \pmatrix{3\\0\\-4} &\\[5pt] &=& 0\cdot3 + (-2)\cdot0 + 0\cdot(-4)&\\[5pt] &=& 0&\\[5pt] \end{array}$

Da das Skalarprodukt Null ergibt, liegt im Punkt $C$ ein rechter Winkel vor.

$\begin{array}[t]{rll} F&=& \dfrac{1}{2} \cdot \mid\overrightarrow{AC}\mid \cdot \mid \overrightarrow{BC} \mid& \\[5pt] &=& \dfrac{1}{2} \cdot \sqrt{(-2)^2 } \cdot \sqrt{3^2 + (-4)^2} & \\[5pt] &=& \dfrac{1}{2} \cdot 2 \cdot 5& \\[5pt] &=& 5 \end{array}$

Der Flächeninhalt der Dreiecksfläche $F$ beträgt $5\,\text{FE}.$

Lösung 5 - Stochastik

$\dfrac{0,2}{0,6}=\dfrac{1}{3}$

Der Anteil der Kunden, die gerne in beide Regionen reisen, ist jeweils im Anteil der Kunden enthalten, die nur in eine der beiden Regionen gerne reisen. Daher lässt sich der gesuchte Anteil wie folgt berechnen:

$0,6+0,3-2\cdot 0,2=0,5=50\,\%$

Lösung 6 - Stochastik

Insgesamt beinhaltet die Urne 8 Kugeln, sodass die Anfangswahrscheinlichkeit für eine rote Kugel $p_r= \dfrac{3}{8}$ und für eine gelbe Kugel $p_g=\dfrac{5}{8}$ beträgt.
Gezogen wird zweimal ohne Zurücklegen, womit sich folgendes Baumdiagramm ergibt:

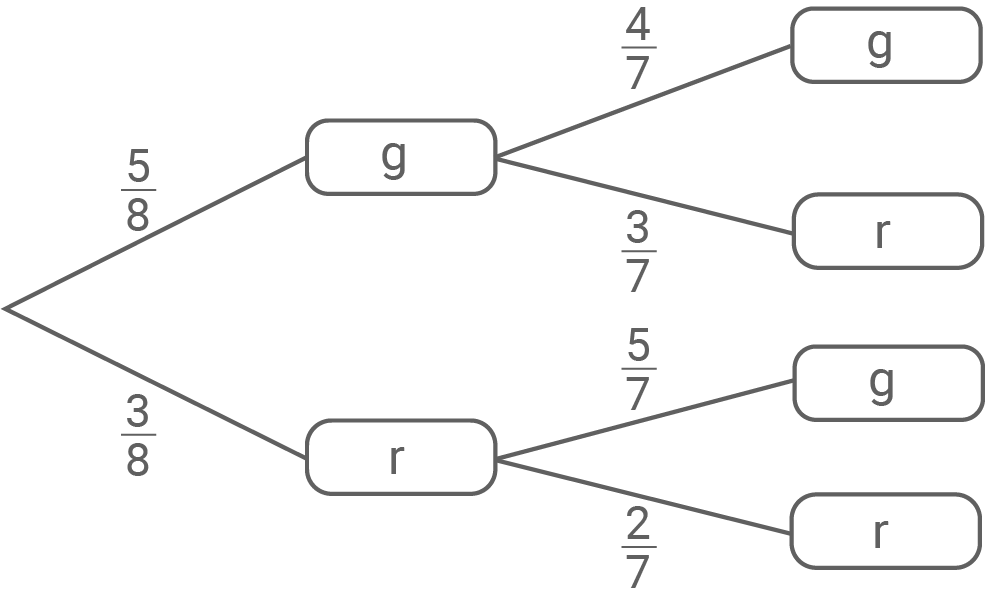Mit der ersten Pfadregel ergibt sich die Wahrscheinlichkeit für das Ereignis $p_1$ :

$p_1 = \dfrac{5}{8} \cdot \dfrac{4}{7}= \dfrac{20}{56} = \dfrac{5}{14}$

Aus dem Baumdiagramm folgt:

$p_2 = \dfrac{4}{7}$

Der Term berechnet die Wahrscheinlichkeit, dass beim fünfmaligen Ziehen mit Zurücklegen genau zwei rote Kugeln gezogen werden.

$\pmatrix{5\\2}$ gibt die Anzahl der Pfade mit 2 roten und 3 grünen Kugeln an.
$\pmatrix{\dfrac{3}{8}}^2$ gibt die Wahrscheinlichkeit dafür an, dass 2 rote Kugeln hintereinander gezogen werden.
$\pmatrix{\dfrac{5}{8}}^3$ gibt die Wahrscheinlichkeit dafür an, dass 3 grüne Kugeln hintereinander gezogen werden.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?