Aufgabe 3

Aufgabenstellung

In einem kartesischen Koordinatensystem sind die Punkte $O(0\mid0\mid0)$ , $A(9\mid12\mid0)$ , $B(-3\mid21\mid0)$ , $C(-12\mid9\mid0)$ und $S(-1,5\mid10,5\mid15)$ Eckpunkte der Pyramide $OABCS,$ deren Grundfläche das Viereck $OABC$ ist (siehe Abbildung).

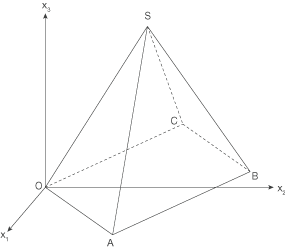Dreidimensionales Diagramm eines Tetraeders mit den Punkten S, A, B, C und O.

Abbildung

Im Folgenden darf verwendet werden, dass die Seitendreiecke der Pyramide zueinander kongruent sind.

a) (1) Zeige, dass das Viereck $OABC$ ein Quadrat ist.

(6P)

(2) Berechne das Volumen und die Oberfläche der Pyramide $OABCS$ .

(8P)

b) (1) Zeige, dass der Punkt $R(5\mid15\mid0)$ auf der Strecke $\overline{AB}$ liegt.

(3P)

(2) Zeige, dass die Strecke $\overline{OR}$ die Grundfläche der Pyramide im Verhältnis $5:1$ bzw. $1:5$ teilt.

(5P)

(3) Leite eine Parameter- und eine Koordinatengleichung der Ebene $E$ her, die durch die Punkte $O$ , $Q(1\mid 1\mid 2)$ und $R$ festgelegt ist.

[Mögliches Ergebnis: $E: 3x_{1}-x_{2}-x_{3}=0]$

(7P)

c) (1) Bestimme die Koordinaten des Schnittpunktes $P$ der Geraden $g$ durch $S$ und $A$ mit der Ebene $E$ aus Aufgabe b) (3).

[Zur Kontrolle: Der Schnittpunkt ist $P(5,5\mid11,5\mid5)$ .]

(6P)

(2) Weise nach, dass die Strecken $\overline{OP}$ und $\overline{BP}$ senkrecht zur Geraden $g$ verlaufen.

(5P)

(3) Begründe, dass der Streckenzug $\overline{OPB}$ ein kürzester Weg von $O$ nach $B$ über den Mantel der Pyramide (Mantel: Oberfläche ohne Grundfläche) ist, und berechne die Länge des Streckenzuges.

(6P)

(4) Es gibt einen weiteren Streckenzug $\overline{ONB}$ $(N\neq P)$ , der ein kürzester Weg von $O$ nach $B$ über den Mantel der Pyramide ist.

Begründe diese Aussage und beschreibe die Lage des Punktes $N$ .

(5P)

a) (1)

$\blacktriangleright$ Zeigen, dass $\boldsymbol{OABC}$ ein Quadrat ist

Hier ist es deine Aufgabe zu zeigen, dass das Viereck $OABC$ ein Quadrat ist. Dazu musst du Folgendes tun:

Verbindungsvektoren, die die Seiten beschreiben, berechnen.

Zeige, dass alle Seiten gleich lang sind.
Die Länge der Seiten kannst du mit den Beträgen der entsprechenden Verbindungsvektoren berechnen.

Zeige, dass jeder Innenwinkel ein rechter Winkel ist.
Dies kannst du mit dem Skalarprodukt zeigen.

Hast du dies getan, so hast du gezeigt, dass $OABC$ ein Quadrat ist.

1. Schritt: Verbindungsvektoren berechnen

Die Seiten des Vierecks sind hier die Strecken $\overline{OA}$ , $\overline{AB}$ , $\overline{OC}$ und $\overline{CB}$ . Berechne die dazugehörigen Verbindungsvektoren:

$\overrightarrow{CB}=\overrightarrow{OB}-\overrightarrow{OC}=\begin{pmatrix}-3\\ 21\\ 0\end{pmatrix} - \begin{pmatrix}-12\\ 9\\ 0\end{pmatrix}=\begin{pmatrix}9\\ 12\\ 0\end{pmatrix}$

$\overrightarrow{OA}=\begin{pmatrix}9\\ 12\\ 0\end{pmatrix}$

$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=\begin{pmatrix}-3\\ 21\\ 0\end{pmatrix} - \begin{pmatrix}9\\ 12\\ 0\end{pmatrix}=\begin{pmatrix}-12\\ 9\\ 0\end{pmatrix}=\overrightarrow{OC}$

Du erkennst außerdem, dass die gegenüberliegenden Seiten $\overline{OA}$ und $\overline{CB}$ bzw. $\overline{OC}$ und $\overline{CB}$ zueinander parallel sind.

2. Schritt: Zeigen, dass alle Seiten gleich lang sind

Zeige hier, dass die Längen aller Verbindungsvektoren gleich sind. Da $\overrightarrow{CB}=\overrightarrow{OA}$ und $\overrightarrow{AB}=\overrightarrow{OC}$ gilt, musst du nur $\left|\overrightarrow{OA}\right| = \left| \overrightarrow{OC} \right|$ zeigen:

$\left|\overrightarrow{OA}\right|=\sqrt{9^2 +12^2 +0}=\sqrt{225}=15$

$\left|\overrightarrow{OC}\right|=\sqrt{(-12)^2+9^2 +0}=\sqrt{225}=15$

Somit sind alle Seiten gleich lang.

3. Schritt: Zeigen, dass jeder Innenwinkel ein rechter Winkel ist

Hier reicht es zu zeigen, dass ein Innenwinkel 90° groß ist bzw. dass die Verbindungsvektoren senkrecht aufeinander stehen. Dies kannst du zeigen, indem du das Skalarprodukt der Vektoren berechnest. Ist das Skalarprodukt zweier Vektoren gleich Null, so stehen die Vektoren senkrecht aufeinander. Da die gegenüberliegenden Seiten parallel sind, kannst du daraus folgern, dass alle Winkel rechte Winkel sind. Wir betrachten im Folgenden also nur $\overrightarrow{OA} \circ \overrightarrow{OC}$ :

$\overrightarrow{OA} \circ \overrightarrow{OC}=\begin{pmatrix}9\\ 12\\0\end{pmatrix} \circ \begin{pmatrix}-12\\ 9\\ 0\end{pmatrix}=9 \cdot (-12) + 12\cdot 9+0=-108 + 108=0$

Damit hast du gezeigt, dass alle Innenwinkel des Vierecks rechte Winkel sind.

Insgesamt folgt daraus, dass das Viereck $OABC$ ein Quadrat ist.

(2)

$\blacktriangleright$ Volumen der Pyramide berechnen

Berechne nun das Volumen $V$ der Pyramide. Das Volumen einer Pyramide ist durch folgende Formel gegeben:

$V=\dfrac{1}{3} \cdot A_G \cdot h_S$

Dabei ist $A_G$ der Flächeninhalt der Grundfläche der Pyramide und $h_S$ die Höhe der Pyramide. Berechne also diese beiden Werte und damit das Volumen der Pyramide.

1. Schritt: Flächeninhalt $\boldsymbol{A_G}$ der Grundfläche der Pyramide berechnen

In Aufgabe (1) hast du bereits gezeigt, dass die Grundfläche ein Quadrat ist und die Seitenlängen berechnet. Also kannst du den Flächeninhalt $A_G$ folgendermaßen berechnen:

$A_G=\left|\overrightarrow{OA}\right|^2=15^2=225$

2. Schritt: Höhe $\boldsymbol{h_S}$ der Pyramide berechnen

Die Grundfläche der Pyramide liegt in der $x_1$ - $x_2$ -Ebene, da die $x_3$ -Koordinate aller Eckpunkte gleich Null ist. Die Höhe der Spitze ist gerade die $x_3$ -Koordinate von der Spitze $S$ . Also ist $h_S=15$

3. Schritt: Volumen $\boldsymbol{V}$ berechnen

Setze die oben berechneten Werte in die Formel ein:

$V=\dfrac{1}{3} \cdot 225 \cdot 15=1.125$

Das Volumen der Pyramide beträgt $1.125$ VE.

$\blacktriangleright$ Oberfläche der Pyramide berechnen

Die Oberfläche $A$ ist wieder durch eine Formel gegeben:

$A=A_G + A_M$

Hier ist $A_G$ wieder der Flächeninhalt der Grundfläche der Pyramide, $A_M$ ist der Flächeninhalt der Mantelfläche der Pyramide. Die Mantelfläche der Pyramide besteht aus den vier Flächen der Seitendreiecke. Der Flächeninhalt der Mantelfläche setzt sich somit aus den Flächeninhalten der Seitendreiecke zusammen. Du kannst verwenden, dass die Seitendreiecke kongruent sind, das heißt ihre Flächeninhalte sind gleich. Für den Flächeninhalt $A_\triangle$ eines Seitendreiecks ist die Mantelfläche durch folgende Formel gegeben:

$A_M=4\cdot A_\triangle$

Berechne also zuerst den Flächeninhalt eine Seitendreiecks. Wähle das Seitendreieck $OAS$ . Du benötigst nun die Höhe und die Länge der Grundseite des Dreiecks $OAS$ . Wähle als Grundseite des Dreiecks die Seite $\overline{OA}$ . Mit der Höhe $h_\triangle$ des Dreiecks kannst du den Flächeninhalt des Dreiecks folgendermaßen berechnen:

$A_\triangle=\dfrac{1}{2} \cdot h_\triangle \cdot \left|\overrightarrow{OA}\right|$

Du musst noch die Höhe $h_\triangle$ berechnen. Betrachte dazu die untenstehende Skizze:

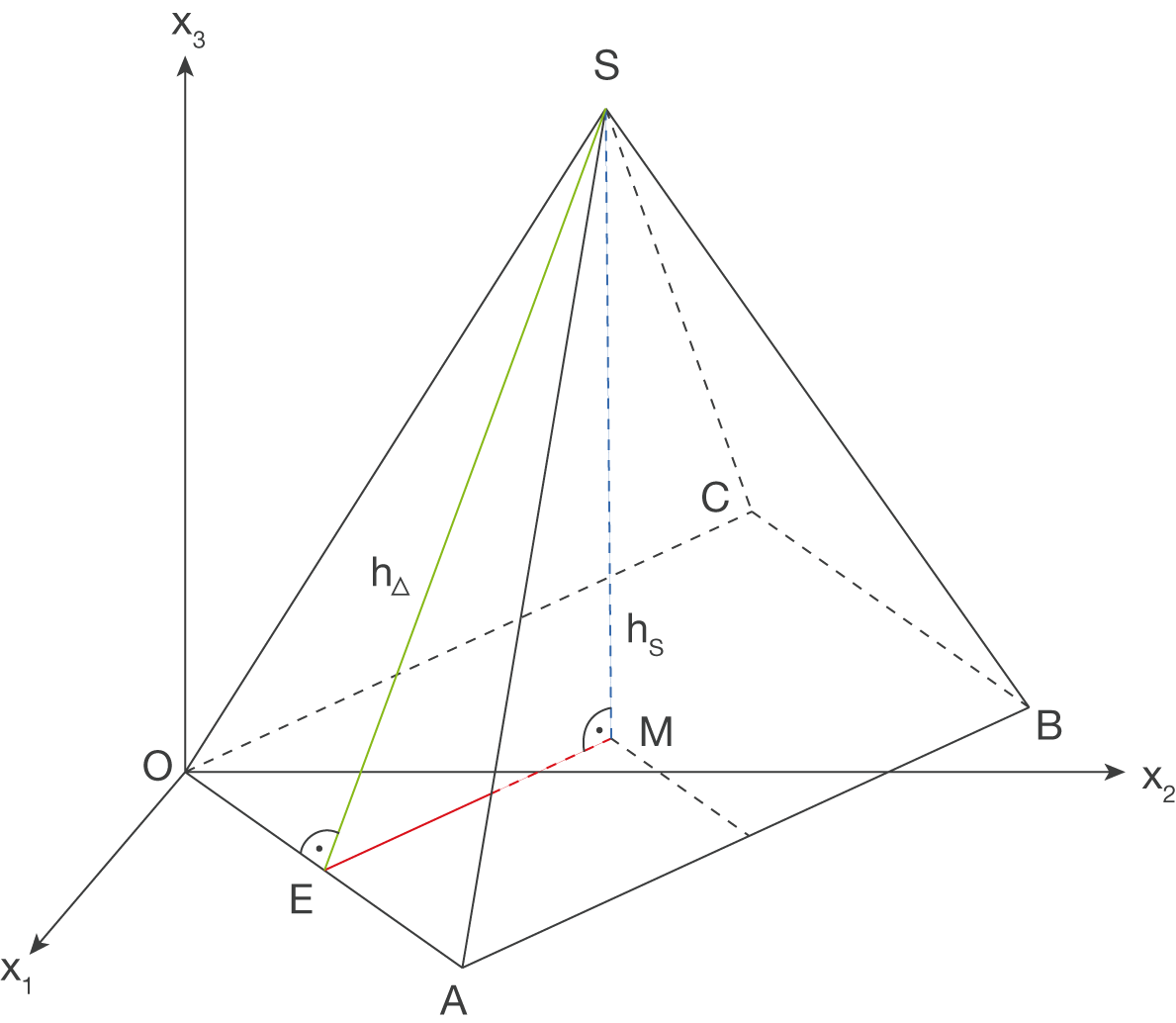Grafische Darstellung eines geometrischen Modells mit Linien und Punkten in einem dreidimensionalen Koordinatensystem.

Das Dreieck mit den Eckpunkten $EMS$ ist rechtwinklig und die Strecke zwischen $E$ und $S$ entspricht der Höhe $h_\triangle$ (grüne Linie). Also kannst du die Höhe $h_\triangle$ mit dem Satz des Pythagoras berechnen.

Die Höhe $h_S$ (blaue Linie) hast du bereits für das Volumen berechnet, es ist $h_S=15$ . Es fehlt nun noch die Länge der Strecke $\overline{EM}$ (rote Linie). Der Punkt $M$ ist gerade der Mittelpunkt der Grundfläche. Diese ist quadratisch und somit ist die Länge der Strecke $\overline{EM}$ die Hälfte der Länge der Seite $\overline{AB}$ . Also gilt:

$\left|\overrightarrow{EM}\right|=\dfrac{1}{2} \cdot \left|\overrightarrow{AB}\right|=\dfrac{1}{2} \cdot 15 = 7,5$

Nun kannst du die Höhe $h_\triangle$ mit dem Satz des Pythagoras ausrechnen:

$h_\triangle^2=h_S^2 + \left|\overrightarrow{EM}\right|^2=15^2 + 7,5^2=225 + 56,25=281,25$

Also: $h_\triangle=\sqrt{281,25}\approx16,77$

Damit kannst du nun die Oberfläche der Pyramide berechnen:

$\begin{array}[t]{rll} A&=A_G+A_M& \quad \scriptsize \; A_M=4 \cdot A_\triangle\\[5pt] &=A_G+4\cdot A_M&\quad \scriptsize \; A_\triangle=\dfrac{1}{2} \cdot h_\triangle \cdot \left|\overrightarrow{OA}\right| \\[5pt] &=A_G + 4 \cdot \dfrac{1}{2} \cdot h_\triangle \cdot \left|\overrightarrow{OA}\right| \\[5pt] &=A_G + 2 \cdot h_\triangle \cdot \left|\overrightarrow{OA}\right| \end{array}$

Hier kannst du die oben berechneten Werte einsetzen:

$\begin{array}[t]{rll} A&=225 + 2 \cdot 16,77 \cdot 15 \\[5pt] &=225 + 503,1 \\[5pt] &=728,1 \end{array}$

Die Oberfläche der Pyramide beträgt $728,1$ FE.

b) (1)

$\blacktriangleright$ Zeigen, dass der Punkt $\boldsymbol{R}$ auf der Strecke $\boldsymbol{\overline{AB}}$ liegt

Hier sollst du zeigen, dass der Punkt $R$ auf der Strecke $\overline{AB}$ liegt. Dies kannst du auf du zwei verschiedene Weisen zeigen: Über die Verbindungsvektoren oder indem du eine Gerade aufstellst.

$\color{#87c800}{\blacktriangleright\blacktriangleright}$ Lösungsweg A: Verbindungsvektoren

Der Punkt $R$ liegt genau dann auf der Strecke $\overline{AB}$ , wenn für die Länge der Verbindungsvektoren folgende Bedingung gilt:

$$ \left|\overrightarrow{AR}\right| +\left| \overrightarrow{RB}\right| = \left|\overrightarrow{AB}\right| $$

Berechne also zuerst die Verbindungsvektoren $\overrightarrow{AR}$ und $\overrightarrow{RB}$ , überprüfe danach die Bedingung mit dem Vektor $\overrightarrow{AB}$ , den du bereits berechnet hast.

$\overrightarrow{AR}=\overrightarrow{OR}-\overrightarrow{OA}=\begin{pmatrix}5\\ 15\\ 0\end{pmatrix} - \begin{pmatrix}9\\ 12\\ 0\end{pmatrix}=\begin{pmatrix}-4\\ 3\\ 0\end{pmatrix}$

$\overrightarrow{RB}=\overrightarrow{OB}-\overrightarrow{OR}=\begin{pmatrix}-3\\ 21\\ 0\end{pmatrix} - \begin{pmatrix}5\\ 15\\ 0\end{pmatrix}=\begin{pmatrix}-8\\ 6\\ 0\end{pmatrix}$

Damit kannst du die Bedingung nachrechnen:

$\begin{array}[t]{rll} \left|\overrightarrow{AR}\right| + \left|\overrightarrow{RB}\right| &=& \left|\begin{pmatrix}-4\\ 3\\ 0\end{pmatrix}\right|+ \left|\begin{pmatrix}-8\\ 6\\ 0\end{pmatrix}\right| \\[5pt] &=& \sqrt{\left(-4\right)^2 + 3^2} + \sqrt{\left(-8\right)^2 + 6^2}\\[5pt] &=& \sqrt{25} + \sqrt{100}\\[5pt] &=& 5 + 10 \\[5pt] &=& 15 \end{array}$

$\begin{array}[t]{rll} \left|\overrightarrow{AB}\right| &=& \begin{pmatrix}-12\\ 9\\ 0\end{pmatrix} \\[5pt] &=& \sqrt{\left(-12\right)^2 + 9^2} \\[5pt] &=&\sqrt{225} \\[5pt] &=&15 \end{array}$

Damit ist die Bedingung erfüllt und der Punkt $R$ liegt auf der Strecke $\overline{AB}$ .

$\color{#87c800}{\blacktriangleright\blacktriangleright}$ Lösungsweg B: Gerade aufstellen

Stelle dazu zuerst die Gerade $h$ durch die Punkte $A$ und $B$ auf:

$h:\; \overrightarrow{x}=\overrightarrow{OA} + s \cdot \overrightarrow{AB}; \; s \in \mathbb{R}$

Die Vektoren $\overrightarrow{OA}$ und $\overrightarrow{AB}$ hast du bereits berechnet. Also ist die Geradengleichung:

$h:\; \overrightarrow{x}=\begin{pmatrix}9\\ 12\\ 0\end{pmatrix} + s \cdot \begin{pmatrix}-12\\ 9\\ 0\end{pmatrix}; \; s \in \mathbb{R}$

Für $s=0$ erhältst du den Ortsvektor des Punktes $A$ , für $s=1$ erhältst du $\overrightarrow{OA} + \overrightarrow{AB} = \overrightarrow{OB}$ , also den Ortsvektor des Punktes $B$ . Für $s \in \left[0;1\right]$ kannst du alle Punkte auf der Strecke $\overline{AB}$ darstellen. Zeige also, dass der Punkt $R$ auf der Geraden $h$ liegt, wobei der Wert von $s$ zwischen 0 und 1 ist. Setze dazu den Ortsvektor von $R$ gleich der Geradengleichung von $h$ :

$\begin{array}[t]{rll} \begin{pmatrix}9\\ 12\\ 0\end{pmatrix} + s \cdot \begin{pmatrix}-12\\ 9\\ 0\end{pmatrix}& = \begin{pmatrix}5\\ 15\\ 0\end{pmatrix}& \quad \scriptsize \mid\; -\begin{pmatrix}9\\ 12\\ 0\end{pmatrix} \\[5pt] s \cdot \begin{pmatrix}-12\\ 9\\ 0\end{pmatrix}&=\begin{pmatrix}-4\\ 3\\ 0\end{pmatrix}& \end{array}$

Die letzte Zeile lautet $0\cdot s = 0$ und ist für jedes $s \in \mathbb{R}$ erfüllt. Betrachte also die erste Zeile. Aus der ersten Zeile kannst du ablesen, dass: $s \cdot \left(-12\right)=-4$ .

$\Rightarrow\; s=\dfrac{-4}{-12}=\dfrac{1}{3}$

Setze dieses Ergebnis in die zweite Zeile ein: $s \cdot 9=\dfrac{1}{3} \cdot 9=3\qquad$ Grünes Häkchen-Symbol auf transparentem Hintergrund.

Der Punkt $R$ liegt also auf der Geraden $h$ . Weiter gilt für den Parameter $s$ , dass $0\leq \dfrac{1}{3} \leq1$ . Also liegt der Punkt $R$ auch auf der Strecke $\overline{AB}$ .

(2)

$\blacktriangleright$ Zeigen, dass die Strecke $\boldsymbol{\overline{OR}}$ die Grundfläche der Pyramide im Verhältnis 1:5 bzw. 5:1 teilt

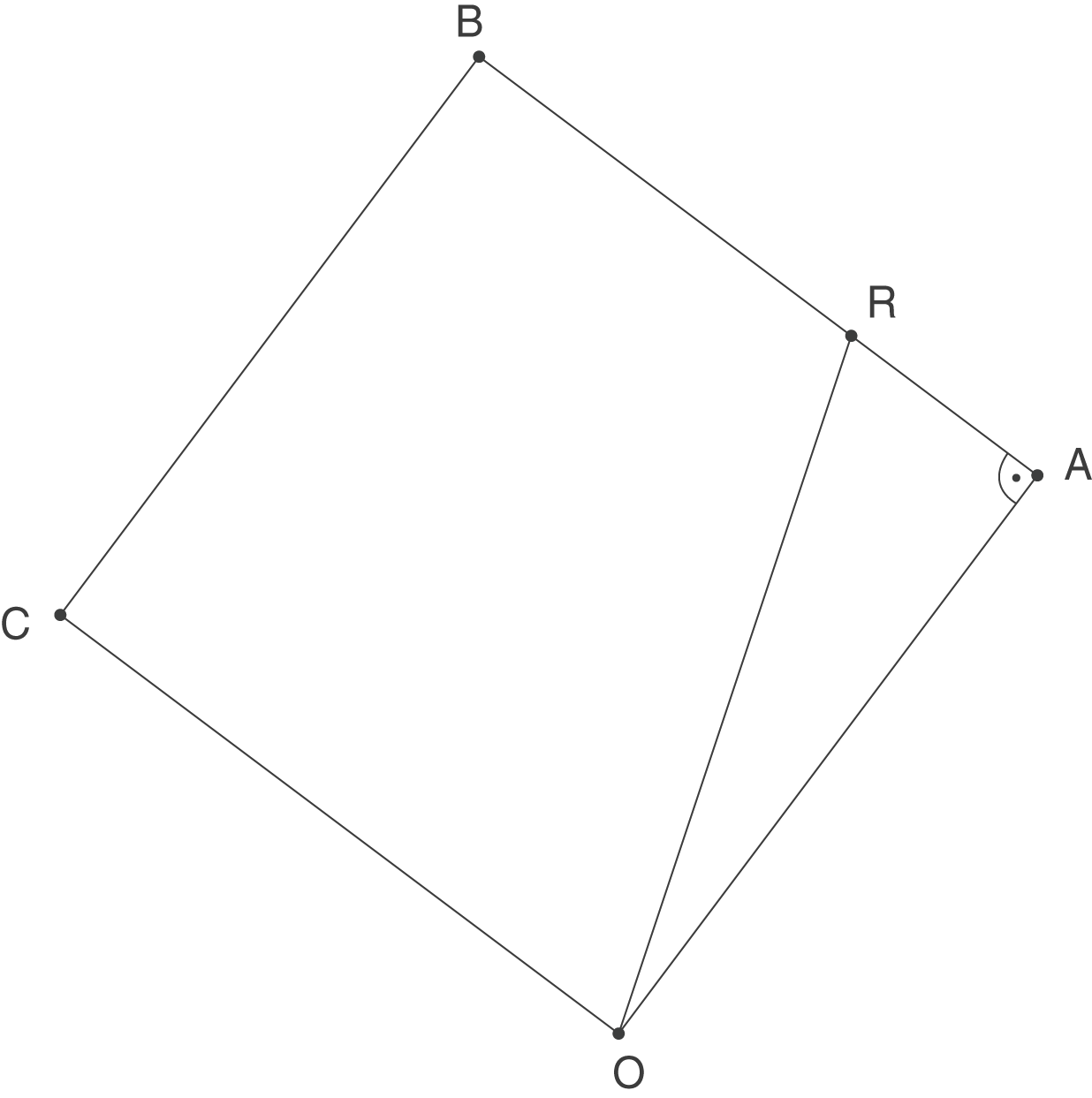Diagramm mit Punkten und Linien, die verschiedene Buchstaben und Farben darstellen.

In der nebenstehenden Skizze erkennst du die Lage des Punktes $R$ . Die Strecke $\overline{OR}$ teilt die Grundfläche in das Dreieck $OAR$ und das Viereck $ORBC$ . Berechne zuerst die Fläche des Dreiecks $OAR$ und die des Vierecks ORBC. Zeige im Anschluss, dass die Flächen im Verhältnis 1:5 stehen.

1. Schritt: Flächeninhalt des Dreiecks $\boldsymbol{OAR}$ berechnen

Um den Flächeninhalt des Dreiecks $OAR$ zu bestimmen, benötigst du eine Grundseite und die dazugehörige Höhe. Hier kannst du die Grundseite $\overline{OA}$ und Höhe $\overline{AR}$ benutzen, da dort ein rechter Winkel voliegt. Berechne zuerst den Vektor $\overrightarrow{AR}$ :

$\overrightarrow{AR}=\overrightarrow{OR}-\overrightarrow{OA}=\begin{pmatrix}5\\ 15\\ 0\end{pmatrix} - \begin{pmatrix}9\\ 12\\ 0\end{pmatrix}=\begin{pmatrix}-4\\ 3\\ 0\end{pmatrix}$

Somit gilt für den Flächeninhalt $A_{OAR}$ :

$\begin{array}[t]{rll} A_{OAR}&=\dfrac{1}{2} \cdot \left|\overrightarrow{OA}\right| \cdot \left|\overrightarrow{AR}\right| \\[5pt] &=\dfrac{1}{2} \cdot 15 \cdot \left( \sqrt{ \left(-4\right)^2+3^2} \right)\\[5pt] &=7,5 \cdot \sqrt{25}\\[5pt] &=7,5 \cdot 5\\[5pt] &=37,5 \end{array}$

2. Schritt: Flächeninhalt des Vierecks $\boldsymbol{ORBC}$ bestimmen

Der Flächeninhalt der Grundfläche beträgt $A_G=225$ . Die Flächeninhalt des Vielecks $ORBC$ kannst du mittels der Differenz der gesamten Fläche und der Dreiecksfläche bestimmen:

$A_{ORBC}=A_G-A_{OAR}=225-37,5=187,5$

3. Schritt: Verhältnis der Flächen bestimmen

Mit den beiden Flächeninhalten kannst du nun das Verhältnis bestimmen:

$\dfrac{A_{OAR}}{A_{ORBC}}=\dfrac{37,5}{187,5}=\dfrac{1}{5}$

Das Verhältnis $A_{OAR}:A_{ORBC}$ entspricht also dem Verhältnis $1:5$ bzw. das Verhältnis $A_{ORBC}:A_{OAR}$ entspricht dem Verhältnis $5:1$ .

(3)

$\blacktriangleright$ Parametergleichung der Ebene $\boldsymbol{E}$ herleiten

Zuerst sollst du eine Parametergleichung der Ebene $E$ herleiten. Die Ebene $E$ ist durch die Punkte $O$ , $Q$ und $R$ festgelegt und du kannst somit eine Gleichung der Ebene in Parameterform aufstellen. Du benötigst dazu einen Stützvektor und zwei Spannvektoren. Als Stützvektor kannst du einen Ortsvektor der drei Punkte auswählen, als Spannvektoren zwei Verbindungsvektoren der drei Punkte. Eine mögliche Gleichung in Parameterform ist:

$E:\; \overrightarrow{x}=\overrightarrow{OO} + t \cdot \overrightarrow{OQ} + s \cdot \overrightarrow{OR}; \quad s,t \in \mathbb{R}$

Der Vektor $\overrightarrow{OO}$ entspricht $\begin{pmatrix}0\\ 0\\ 0\end{pmatrix}$ , du kannst ihn auch weglassen. Die beiden Spannvektoren sind durch die Koordinaten der Punkte $Q$ und $R$ festgelegt. Somit lautet eine Ebenengleichung in Parameterform:

$E:\; \overrightarrow{x}=t \cdot \begin{pmatrix}1\\ 1\\ 2\end{pmatrix} + s \cdot \begin{pmatrix}5\\ 15\\ 0\end{pmatrix}; \quad s,t \in \mathbb{R}$

$\blacktriangleright$ Koordinatengleichung der Ebene $\boldsymbol{E}$ herleiten

Leite nun eine Koordinategleichung der Ebene $E$ her. Dazu benötigst du einen Normalenvektor $\overrightarrow{n}$ der Ebene $E$ . Hast du einen Normalenvektor $\overrightarrow{n}$ der Ebene gegeben, so lautet eine Gleichung in Koordinatenform:

$H:\, n_1 \cdot x_1 + n_1 \cdot x_1 + n_1 \cdot x_1 = d; \quad d\in \mathbb{R}$ .

Berechne also mit dem Kreuzprodukt einen Normalenvektor $\overrightarrow{n}$ der Ebene $E$ . Mit diesem kannst du dann eine Gleichung der Ebene $E$ in Koordinatenform angeben und den Parameter $d$ mit einer Punktprobe bestimmen.

$\overrightarrow{n}=\overrightarrow{OQ} \times \overrightarrow{OR}=\begin{pmatrix}1\\ 1\\ 2\end{pmatrix} \times \begin{pmatrix}5\\ 15\\ 0\end{pmatrix}=\begin{pmatrix}0 - 2\cdot 15\\ 2\cdot 5 - 0\\ 1\cdot 15 - 1 \cdot 5\end{pmatrix}=\begin{pmatrix}-30\\ 10\\ 10\end{pmatrix}= 10 \cdot \begin{pmatrix}-3\\ 1\\ 1\end{pmatrix}$

Die nur die Richtung und nicht die Länge des Normalenvektors relevant ist, kannst du hier den durch $10$ gekürzten Vektor als Normalenvektor verwenden:

$\begin{array}{lrlll} E:& 3 \cdot x_1 - x_2 - x_3&=&d \end{array}$

Bestimme $d$ mit einer Punktprobe. Setze einen Punkt der Ebene, zum Beispiel $O$ , ein. Du erhältst $0=d$ . Damit lautet eine Koordinatengleichung der Ebene $E$ :

$E:\; 3 \cdot x_1 - x_2 - x_3=0$

c) (1)

$\blacktriangleright$ Koordinaten des Schnittpunkts $\boldsymbol{P}$ bestimmen

Hier ist deine Aufgabe, die Koordinaten des Schnittpunkts $P$ der Ebene $E$ und der Geraden $g$ zu bestimmen. Dazu musst du zuerst eine Geradengleichung der Geraden $g$ bestimmen. Hast du dies getan, so kannst du den Schnittpunkt $P$ mit dem Einsetzungs- oder Gleichsetzungsverfahren bestimmen, indem du jeweils nach dem Parameter $r$ auflöst und damit die Koordinaten des Punktes $P$ bestimmen kannst.

1. Schritt: Geradengleichung der Gerade $\boldsymbol{g}$ bestimmen

Die Gerade $g$ geht durch die Punkte $S$ und $A$ . Somit kannst du folgende Geradengleichung aufstellen:

$g: \overrightarrow{x}=\overrightarrow{OA} + r \cdot \overrightarrow{AS}$

Den Vektor $\overrightarrow{OA}$ kennst du bereits. Berechne also noch $\overrightarrow{AS}$ :

$\overrightarrow{AS}=\overrightarrow{OS}-\overrightarrow{OA}=\begin{pmatrix}-1,5\\ 10,5\\ 15\end{pmatrix} - \begin{pmatrix}9\\ 12\\ 0\end{pmatrix} = \begin{pmatrix}-10,5\\ -1,5 \\ 15\end{pmatrix}$

Damit lautet eine Geradengleichung der Gerade $g$ :

$g:\; \overrightarrow{x}=\begin{pmatrix}9\\ 12\\ 0\end{pmatrix}+ r \cdot \begin{pmatrix}-10,5\\ -1,5\\ 15\end{pmatrix}=\begin{pmatrix}9 -10,5 \cdot r\\ 12 - 1,5 \cdot r\\ 15 \cdot r\end{pmatrix}$

2. Schritt: Schnittpunkt $\boldsymbol{P}$ bestimmen

Du kannst den Schnittpunkt $P$ mit dem Einsetzungs- oder Gleichsetzungsverfahren bestimmen.

$\color{#87c800}{\blacktriangleright\blacktriangleright}$ Lösungsweg A: Einsetzungverfahren

Um den Schnittpunkt mit dem Einsetzungsverfahren zu bestimmen, setzt die Koordinaten der Gleichung zu $g$ in die Koordinatengleichung der Ebene $E$ und löst nach dem Parameter $r$ auf:

$\begin{array}[t]{rll} 3 \cdot \left( 9-10,5\cdot r \right)- \left(12 - 1,5 \cdot r\right) - \left(15 \cdot r\right)&=0 & \\[5pt] 27 - 31,5 \cdot r - 12 + 1,5 \cdot r - 15 \cdot r&=0 & \\[5pt] 15 - 45\cdot r &=0 &\quad \mid\; +45 \cdot r \\[5pt] 15&=45\cdot r & \quad \mid\; :45 \\[5pt] \dfrac{1}{3}&=r \end{array}$

Setze $r=\dfrac{1}{3}$ in die Geradengleichung von $g$ ein, um den Ortsvektor des Schnittpunkts $P$ zu erhalten:

$\overrightarrow{OP}=\begin{pmatrix}9\\ 12\\ 0\end{pmatrix}+ \dfrac{1}{3} \cdot \begin{pmatrix}-10,5\\ -1,5\\ 15\end{pmatrix} = \begin{pmatrix}9\\ 12\\ 0\end{pmatrix}+\begin{pmatrix}-3,5\\ -0,5\\ 5\end{pmatrix} = \begin{pmatrix}5,5\\ 11,5\\ 5\end{pmatrix}$

Du kannst nun die Koordinaten des Schnittpunkts $P$ ablesen. Der Schnittpunkt ist $P(5,5 \mid 11,5 \mid 5)$ .

$\color{#87c800}{\blacktriangleright\blacktriangleright}$ Lösungsweg B: Gleichsetzungsverfahren

Um den Schnittpunkt mit dem Gleichsetzungsverfahren zu bestimmen, setze die Geradengleichung der Geraden $g$ mit der Parametergleichung der Ebene $E$ gleich und löse nach dem Parameter $r$ (und/oder $s$ und $t$ ) auf:

$\begin{array}[t]{rll} \begin{pmatrix}9\\ 12\\ 0\end{pmatrix}+ r \cdot \begin{pmatrix}-10,5\\ -1,5\\ 15\end{pmatrix}&=t \cdot \begin{pmatrix}1\\ 1\\ 2\end{pmatrix} + s \cdot \begin{pmatrix}5\\ 15\\ 0\end{pmatrix}& \quad \scriptsize \mid\; + r \cdot \begin{pmatrix}10,5\\ 1,5\\ -15\end{pmatrix} \\[5pt] \begin{pmatrix}9\\ 12\\ 0\end{pmatrix}&=t \cdot \begin{pmatrix}1\\ 1\\ 2\end{pmatrix} + s \cdot \begin{pmatrix}5\\ 15\\ 0\end{pmatrix} + r \cdot \begin{pmatrix}10,5\\ 1,5\\ -15\end{pmatrix}& \end{array}$

Diese Gleichung kannst du nun als lineares Gleichungssystem schreiben:

$\begin{array}{lrlrlrll} \text{I}\quad&t &+ &5 \cdot s& + &10,5 \cdot r&=9&\\ \text{II}\quad&t &+& 15 \cdot s &+& 1,5 \cdot r&=12&\quad \scriptsize\mid\;\text{Rechne: }\text{II}-\text{I}\\ \text{III}\quad&2 \cdot t &+& 0& +&(-15) \cdot r&=0&\quad \scriptsize\mid\;\text{Rechne: }\text{III}- 2 \cdot \text{I}\\ \hline \text{I}\quad&t &+ &5 \cdot s& + &10,5 \cdot r&=9&\\ \text{IIa}\quad&&& 10 \cdot s &+& (-9) \cdot r&=3&\\ \text{IIIa}\quad& && (-10) \cdot s& +& (-36) \cdot r&=-18&\quad \scriptsize\mid\;\text{Rechne: }\text{IIIa}+ \text{IIa}\\ \hline \text{I}\quad&t &+ &5 \cdot s& + &10,5 \cdot r&=9&\\ \text{IIa}\quad&&& 10 \cdot s &+& (-9) \cdot r&=3&\\ \text{IIIb}\quad& && & & (-45) \cdot r&=-15&\quad \Rightarrow r=\frac{1}{3}\\ \end{array}$

Du kannst nun $r$ in die Geradengleichung von $g$ einsetzen oder das lineare Gleichungssystem weiter nach $s$ und $t$ auflösen und diese in die Ebenengleichung in Parameterform einsetzen ( $s=0,6$ und $t=2,5$ ). Setze hier $r$ in die Geradengleichung ein:

Du kannst nun die Koordinaten des Schnittpunkts $P$ ablesen. Der Schnittpunkt ist $P(5,5 \mid 11,5 \mid 5)$ .

(2)

$\blacktriangleright$ Orthogonalität nachweisen

Weise hier nach, dass die Strecken $\overline{OP}$ bzw. $\overline{BP}$ orthogonal auf der Geraden $g$ stehen. Die Strecken $\overline{OP}$ bzw. $\overline{BP}$ kannst du durch die Vektoren $\overrightarrow{OP}$ bzw. $\overrightarrow{BP}$ darstellen. Stehen die Vektoren senkrecht auf dem Richtungsvektor der Geraden $g$ , so stehen die Strecken senkrecht auf der Geraden. Zwei Vektoren stehen genau dann senkrecht aufeinander, wenn ihr Skalarprodukt gleich Null ist. Berechne also das Skalarprodukt der Vektoren $\overrightarrow{OP}$ bzw. $\overrightarrow{BP}$ und dem Richtungsvektor $\overrightarrow{AS}$ :

$\color{#87c800}{\blacktriangleright}$ Strecke $\overline{OP}$ :

$\overrightarrow{OP} \circ \overrightarrow{AS}=\begin{pmatrix}5,5\\ 11,5\\ 5\end{pmatrix} \circ \begin{pmatrix}-10,5\\ -1,5\\ 15\end{pmatrix}=5,5 \cdot (-10,5) + 11,5 \cdot (-1,5) + 5\cdot 15\\ = -57,75 - 17,25 +75 = 0$

Die Vektoren $\overrightarrow{OP}$ und $\overrightarrow{AS}$ stehen senkrecht aufeinander, also steht die Strecke $\overline{OP}$ senkrecht auf der Geraden $g$ .

$\color{#87c800}{\blacktriangleright}$ Strecke $\overline{BP}$ :

Berechne hier zuerst den Verbindungsvektor $\overrightarrow{BP}$ :

$\overrightarrow{BP}=\overrightarrow{OP}-\overrightarrow{OB}=\begin{pmatrix}5,5\\ 11,5\\ 5\end{pmatrix} - \begin{pmatrix}-3\\ 21\\ 0\end{pmatrix}=\begin{pmatrix}8,5\\ -9,5\\ 5\end{pmatrix}$

Nun kannst du das Skalarprodukt berechnen:

$\overrightarrow{BP} \circ \overrightarrow{AS}=\begin{pmatrix}8,5\\ -9,5\\ 5\end{pmatrix} \circ \begin{pmatrix}-10,5\\ -1,5\\ 15\end{pmatrix}=8,5 \cdot (-10,5) + (-9,5) \cdot (-1,5) + 5\cdot 15 \\= -89,25 + 14,25 +75 = 0$

Die Vektoren $\overrightarrow{BP}$ und $\overrightarrow{AS}$ stehen senkrecht aufeinander, also steht die Strecke $\overline{BP}$ senkrecht auf der Geraden $g$ .

(3)

$\blacktriangleright$ Begründen, dass $\boldsymbol{\overline{OPB}}$ ein kürzester Weg ist

Willst du vom Punkt $O$ zum Punkt $B$ über den Mantel der Pyramide gehen, so kannst du dorthin entweder über die Kante $\overline{AS}$ oder $\overline{CS}$ gehen. Da die Pyramide symmetrisch ist, ist es egal, welche Seite du wählst. Gehst du über die Kante $\overline{AS}$ , wählst du jeweils die kürzesten Wege von $O$ nach $\overline{AS}$ und von $\overline{AS}$ nach $B$ .

Der kürzeste Weg von einem Punkt zu einer Geraden ist die Strecke, die senkrecht auf der Geraden steht. In Teilaufgabe (2) hast du gezeigt, dass die Strecken $\overline{OP}$ und $\overline{BP}$ senkrecht zur Geraden $g$ verlaufen. Die Kante $\overline{AS}$ liegt auf der Geraden $g$ und der Punkt $P$ liegt auf der Kante $\overline{AS}$ . Also kannst du von $O$ über $P$ nach $B$ auf dem Mantel der Pyramide gehen. Der Streckenzug $\overline{OPB}$ ist somit ein kürzester Weg von $O$ nach $B$ .

$\blacktriangleright$ Länge des Streckenzugs berechnen

Die Länge des Streckenzugs $\overline{OPB}$ entspricht der Summe der Längen der Strecken $\overline{OP}$ und $\overline{PB}$ . Die Längen der Strecken $\overline{OP}$ bzw. $\overline{PB}$ sind die Längen der Verbindungsvektoren $\overrightarrow{OP}$ bzw. $\overrightarrow{PB}$ . Berechne also die Längen der Vektoren $\overrightarrow{OP}$ und $\overrightarrow{PB}$ und addiere diese, um die Länge des Streckenzugs zu erhalten.

$\left|\overrightarrow{OP}\right|=\left|\begin{pmatrix}5,5\\ 11,5\\ 5\end{pmatrix}\right|=\sqrt{5,5^2 +11,5^2 + 5^2}= \sqrt{187,5}$

$\left|\overrightarrow{PB}\right|=\left|\begin{pmatrix}8,5\\ -9,5\\ 5\end{pmatrix}\right|=\sqrt{8,5^2 +(-9,5)^2 + 5^2}= \sqrt{187,5}$

Somit gilt für die Länge des Streckenzugs:

$\left|\overline{OPB}\right|=\left|\overrightarrow{OP}\right| + \left|\overrightarrow{PB}\right|= \sqrt{187,5} + \sqrt{187,5} \approx 27,39$

Der Streckenzug $\overline{OPB}$ hat die Länge $27,39$ LE.

(4)

$\blacktriangleright$ Begründen, dass es einen weiteren kürzesten Streckenzug gibt

Willst du vom Punkt $O$ zum Punkt $B$ über den Mantel der Pyramide gehen, so kannst du dorthin entweder über die Kante $\overline{AS}$ oder $\overline{CS}$ gehen. In Teilaufgabe (3) gehst über die „vordere Hälfte“, also die Kante $\overline{AS}$ und den Punkt $P$ . Jedoch kannst du auch über die „hintere Hälfte“, also die Kante $\overline{CS}$ , gehen. Da die Pyramide symmetrisch ist, sind beide Wege gleich lang. Somit gibt es einen weiteren kürzesten Weg über die Kante $\overline{CS}$ und einen Punkt $N$ , der auf dieser Kante liegt.

$\blacktriangleright$ Lage des Punktes $\boldsymbol{N}$ beschreiben

Die Lage des Punktes $N$ kannst du hier mit Hilfe der Symmetrie der Pyramide beschreiben. Wie bereits oben beschrieben, liegt der Punkt $N$ auf der Kante $\overline{CS}$ . Da die Pyramide symmetrisch ist, befindet sich der Punkt $N$ „gegenüber“ vom Punkt $P$ . „Gegenüber“ bedeutet hier an der Mittelachse gespiegelt. Somit hat der Punkt $N$ dieselbe Höhe wie der Punkt $P$ und ist dadurch eindeutig bestimmt.