Aufgabe 5

Reisen mit dem Fernbus werden immer beliebter. Reiseanbieter werben mit günstigen Preisen und besonderem Komfort.

Für eine Städtereise stellt ein Busunternehmen einen Fernbus mit $59$ Plätzen bereit, die vor Reiseantritt gebucht und bezahlt werden. Im Mittel werden $95\,\%$ der Buchungen angetreten.

(1)

Erläutere, unter welcher Voraussetzung die Anzahl der angetretenen Buchungen bei einer Reise als binomialverteilt mit $p=0,95$ angenommen werden kann.

(2)

Die Anzahl der angetretenen Buchungen wird als binomialverteilt mit $p=0,95$ vorausgesetzt. Für einen bestimmten Reisetermin sind genau $59$ Buchungen vorgenommen worden.

Bestimme jeweils die Wahrscheinlichkeit für folgende Ereignisse:

$E_1$ : Genau $59$ Buchungen werden angetreten.

$E_2$ : Mindestens $55$ Buchungen werden angetreten.

$E_3$ : Mehr als $6$ Buchungen werden nicht angetreten.

(3)

Obwohl Buchungen insgesamt mit einer Wahrscheinlichkeit von $5 \,\%$ nicht angetreten werden, treten Reisende unter $50$ Jahren eine Buchung deutlich häufiger nicht an als Reisende über $50$ Jahren. [Reisende, die genau $50$ Jahre alt sind, werden zur Gruppe der Reisenden über $50$ Jahren gezählt.]
Die Wahrscheinlichkeit, dass eine Buchung nicht angetreten wird, betrage bei Reisenden unter $50$ Jahren $6\,\%$ , bei Reisenden über $50$ Jahren nur $2\,\%.$

(i)

Gib auf den waagerechten Strichen die fehlenden Wahrscheinlichkeiten im folgenden Baumdiagramm an.

$U50$ : Reisende unter 50 Jahren	$A$ : Antreten der Buchung
$Ü50$ : Reisende über 50 Jahren	$\overline{A}$ : Nichtantreten der Buchung

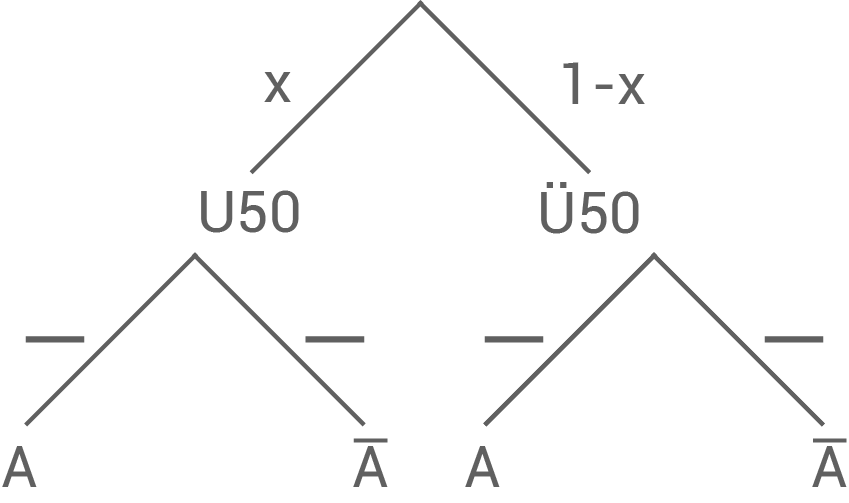
(ii)

Ein Reisender wird zufällig ausgewählt.
Ermittle die Wahrscheinlichkeit $x,$ dass es sich um einen Reisenden unter $50$ Jahren handelt.

[Kontrolllösung: $x=0,75$ ]

(iii)

Ermittle die Wahrscheinlichkeit, dass es sich bei der Buchung eines Reisenden, der die Buchung nicht antritt, um einen Reisenden unter $50$ Jahren handelt.

(3 + 9 + 8 Punkte)

Da erfahrungsgemäß nicht alle Buchungen angetreten werden, verkauft das Busunternehmen mehr Plätze als vorhanden sind. Für eine Städtereise mit $96$ Plätzen werden $99$ Buchungen vorgenommen (Überbuchung). Vereinfachend wird wieder angenommen, dass die Anzahl der angetretenen Buchungen binomialverteilt mit $p=0,95$ ist.

(1)

Ermittle die Wahrscheinlichkeit, dass mindestens eine Person ihre Reise wegen Überbuchung nicht antreten kann.

Kann eine Person die Reise wegen Überbuchung nicht antreten, wird vom Busunternehmen der komplette Reisepreis von $20$ Euro zurückerstattet. Als Entschädigung wird zusätzlich ein Betrag von $300$ Euro ausgezahlt.

(2)

Das Busunternehmen erfasst Werte zur Überbuchung in der folgenden Tabelle.
Ermittle die in der Tabelle fehlende Werte.

Anzahl der Personen, die wegen Überbuchung nicht antreten können	$1$	$2$	$3$
Anzahl $k$ der angetretenen Buchungen	$97$	$98$	$99$
$P_{99; 0,95}(X=k)$
Kosten für Erstattung und Entschädigung in $\,€$	$320$

(3)

Beurteile, ob sich aus finanzieller Sicht die Praxis, $99$ Buchungen für eine Reise mit $96$ Plätzen zu bestätigen, für das Busunternehmen im Mittel lohnt.

(3 + 5 + 4 Punkte)

In der Werbung eines anderen Busunternehmens werden bisher Kunden damit gewonnen, dass bis kurz vor Reiseantritt eine kostenlose Stornierung der Buchung möglich ist. Aktuell liegt der Anteil der kurzfristig stornierten Buchungen bei $7 \,\% .$
Das Busunternehmen ändert die Vertragsbedingungen dahingehend, dass bei kurzfristigen Stornierungen ein Teil des Fahrpreises gezahlt werden muss. Es geht davon aus, dass durch diese Maßnahme der Anteil der kurzfristig stornierten Buchungen sinkt.
Die nächsten $1000$ Buchungen sollen auf diese Wirkung hin untersucht werden. Die Anzahl der kurzfristig stornierten Buchungen wird als binomialverteilt angenommen.
Falls weniger als $55$ Buchungen kurzfristig storniert werden, geht das Busunternehmen davon aus, dass die Maßnahme erfolgreich ist.

(1)

Ermittle die Wahrscheinlichkeit, dass die Maßnahme als erfolgreich angesehen wird, obwohl sich der Anteil der Buchungen, die kurzfristig storniert werden, nicht verändert hat.

(2)

Angenommen, die Maßnahme habe Erfolg gehabt und es gelte $p=0,04.$
Bestimme für $n=1000$ und $p=0,04$ die Wahrscheinlichkeit $P_{1000;0,04}(X\geq 55)$ und erkläre deren Bedeutung im Sachkontext.

(3 + 5 Punkte)

(1)

Jede Buchung wird mit der Wahrscheinlichkeit $p=0,95$ angetreten. Die Anzahl der angetretenen Buchungen kann als binomialverteilt angesehen werden, weil jede Buchung unabhängig von anderen Buchungen angetreten wird.

(2)

$X$ ist binomialverteilt und stellt die Anzahl der angetretenen Buchungen dar. Dann gilt:

$P(E_1)= P_{59;0,95}(X=59) \approx 0,0485$

$P(E_2) = P_{59;0,95}(X\geq 55) \approx 0,8281$

$P(E_3)=P_{59;0,95}(X \leq 52) \approx 0,0274$

(3)

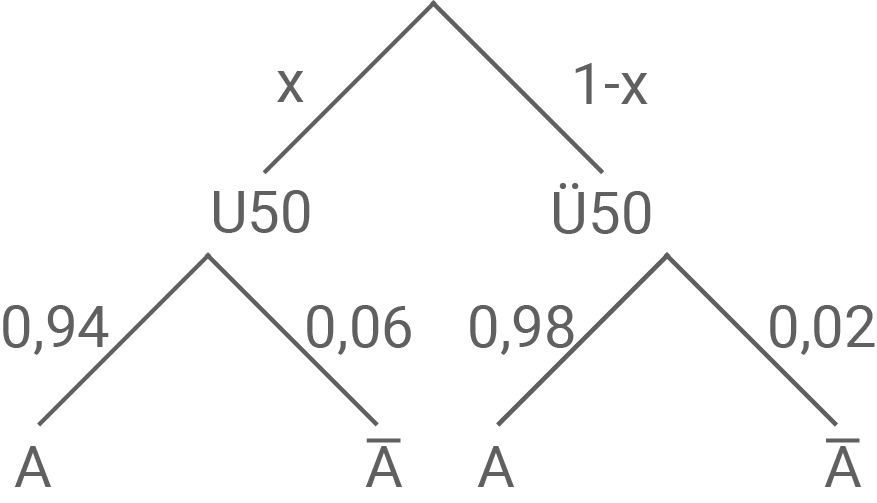
Das Baumdiagramm sieht ergänzt wie folgt aus:

$U50$ : Reisende unter $50$ Jahren
$Ü50$ : Reisende über $50$ Jahren
$A$ : Antreten der Buchung
$\overline{A}$ : Nichtantreten der Buchung

Es werden insgesamt $5\;\text{%}$ der Buchungen nicht angetreten. Daraus ergibt sich aus dem Baumdiagramm:

$\begin{array}[t]{rll} 0,06 \cdot x + 0,02 \cdot (1-x)&=& 0,05&\quad \scriptsize \; \\[5pt] 0,04 \cdot x&=&0,03 &\quad \scriptsize \; \\[5pt] x&=&0,75 \end{array}$

Die Wahrscheinlichkeit, dass es sich um einen Reisenden unter $50$ Jahren handelt, beträgt $0,75$ , also $75\;\text{%}.$

(1)

Mit $X$ : Anzahl der angetretenen Buchungen ist die Wahrscheinlichkeit

$P_{99; 0,95}(X\geq 97) \approx 0,1225$ .

(2)

Tabelle anzeigen

$Anzahl \, der \, Personen, \, die \, wegen \, Überbuchung \, nicht \, antreten \, konnten$	$Anzahl \, k \, der \, angetretenen \, Buchungen$	$P_{99, 0,95} (x=k)$	$Kosten \, für \, Erstattung \, und \, Entschädigung \, in \, Euro$
$1$	$97$	$0,0837$	$320$
$2$	$98$	$0,0325$	$640$
$3$	$99$	$0,0062$	$960$

(3)

Die erwarteten Kosten belaufen sich auf

$K \approx 53,54 \,€$

Vollständige Lösung anzeigen

Zusatzeinnahmen durch Überbuchung : $E= 3 \cdot 20\,€ =60\,€$

Es entsteht ein Gewinn von $6,46 \,€$ für das Busunternehmen. Somit lohnt sich die Praxis aus finanzieller Sicht im Mittel.

(1)

$X$ : Anzahl der Buchungen, die kurzfristig storniert werden.

$P_{1000;0,07} (X\leq54)\approx 0,0241$

(2)

Es ist $P_{1000; 0,04} (X\geq55)\approx 0,0124$ .

Werden 4% der Buchungen storniert und von 1000 Buchungen 55 oder mehr Buchungen storniert, so geht das Busunternehmen mit der Wahrscheinlichkeit $P_{1000; 0,04} (X\geq55)$ dann irrtümlicherweise von einem ausbleibenden Erfolg der Maßnahme aus.