Analysis 1

Unter der Körpertemperatur eines Menschen versteht man die Temperatur des Körperinneren.
Die Körpertemperatur eines gesunden Menschen (Normaltemperatur) wird mit $37,0^{\circ}C$ angenommen.
Bei Temperaturen ab $37,9 ^{\circ} \text {C}$ spricht man von Fieber.

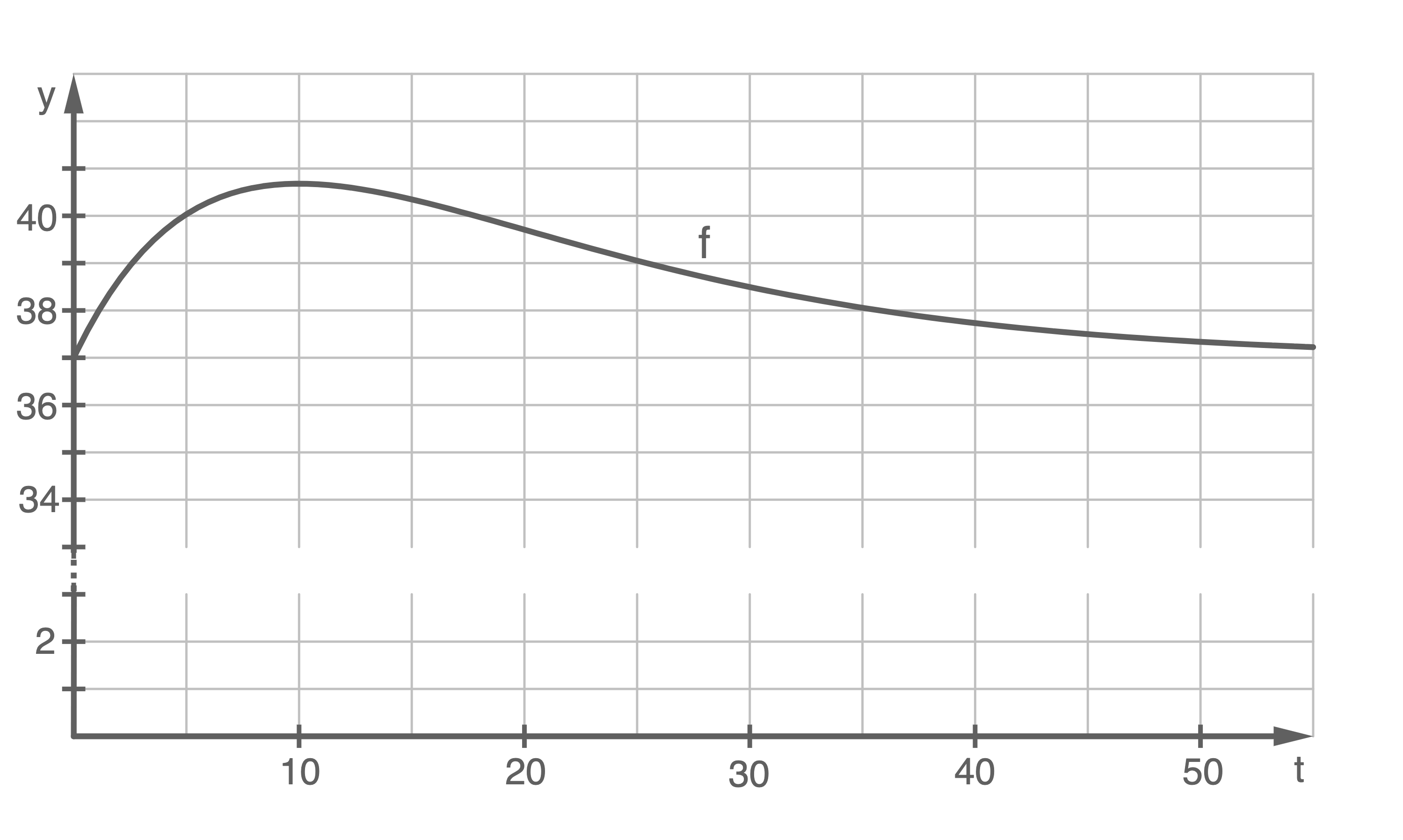Temperatur Verlauf Hessen Mathe Abi 2016

Der zeitliche Verlauf der Körpertemperatur einer erkrankten Person lässt sich bei bestimmten Erkrankungen modellhaft mithilfe der Funktion $f$ mit $f(t)=37+t\cdot \mathrm e^{-0,1\cdot t},\; t\geq 0$ , beschreiben.
Dabei ist $t$ die Zeit in Stunden nach dem Ausbruch der Krankheit und $f(t)$ die Körpertemperatur in $^{\circ} \text C$ .

Die zu ermitttelnden Zeiten sollen in Stunden, auf eine Nachkommastelle gerundet, angegeben werden.

Berechne

die Körpertemperatur bei Ausbruch der Krankheit.
die durchschnittliche Temperaturänderung in den ersten 5 Stunden.
die maximale Körpertemperatur der erkrankten Person.

(6 Punkte)

Berechne $f‘(2)$ und deute diesen Wert im Sachzusammenhang.

(4 Punkte)

Ermittle den Zeitpunkt, zu dem die Körpertemperatur der erkrankten Person am stärksten abnimmt.

(4 Punkte)

Hat eine Person Fieber, wird der Inhalt der Fläche zwischen dem Graphen von $f$ und der Geraden zu $y=37,9$ als ein Maß für die Belastung der erkrankten Person angenommen.

Bestimme den Wert der Belastung für den gesamten Zeitraum, in dem die erkrankte Person Fieber hat.

(5 Punkte)

Ermittle den Zeitpunkt, an dem die Belastung der erkrankten Person den Wert von 25 überschreitet.

(5 Punkte)

Die erkrankte Person nimmt 20 Stunden nach Ausbruch der Krankheit ein fiebersenkendes Medikament ein.

Man geht davon aus, dass ab diesem Zeitpunkt die Temperatur linear abnimmt. Dabei nimmt die Temperatur im linearen Modell doppelt so schnell ab wie die Temperatur nach 20 Stunden in dem durch $f$ beschriebenen Modell.

Berechne, wie viel früher die erkrankte Person mit Medikamenteneinnahme fieberfrei ist.

(6 Punkte)

Die Funktion $f$ wird jetzt unabhängig vom Sachzusammenhang betrachtet.

Durch jeden Punkt $P(p \mid f(p))$ , $p \geq 0$ , verläuft eine Tangente an den Graphen von $f.$

Für jeden Wert von $p$ wird die Tangente durch folgende Gleichung beschrieben:

Gleichung anzeigen

Zeige, dass es genau eine Tangente mit kleinstem $y$ -Achsenabschnitt und genau eine Tangente mit größtem $y$ -Achsenabschnitt gibt.

(5 Punkte)

(35 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Körpertemperatur bei Ausbruch der Krankheit berechnen

$\begin{array}[t]{rll} f(0) &=& 37+ 0\cdot \mathrm e^{-0,1\cdot 0} \\[5pt] &=& 37 \end{array}$

Beim Ausbruch der Krankheit beträgt die Körpertemperatur $37^{\circ}C.$

Durchschnittliche Temperaturänderung berechnen

$\begin{array}[t]{rll} \overline{m} &=& \dfrac{f(5)-f(0)}{5-0} \\[5pt] &=& \dfrac{37+5\cdot \mathrm e^{-0,1\cdot 5}-37}{5} \\[5pt] &\approx& 0,61 \left[\dfrac{^{\circ}C}{\text{h}}\right] \end{array}$

In den ersten $5$ Stunden steigt die Körpertemperatur somit durchschnittlich um ca. $0,61^{\circ}C$ pro Stunde an.

Maximale Körpertemperatur berechnen

Die maximale Körpertemperatur der erkrankten Person entspricht dem Maximum des Graphen von $f.$

1. Schritt: Ableitungsfunktionen bestimmen

Mit der Produktregel folgt:

$\(\begin{array}[t]{rll} f$

$\( f$

Rechenweg anzeigen

2. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

3. Schritt: Hinreichende Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

4. Schritt: $y$ -Koordinate berechnen

$\begin{array}[t]{rll} f(10)&=& 37 + 10\cdot \mathrm e^{-0,1\cdot 10}\\[5pt] &=& 37 +10 \cdot \mathrm e^{-1} \\[5pt] &\approx& 40,68\; [^{\circ}C] \end{array}$

Die maximale Körpertemperatur der erkrankten Person beträgt ca. $40,68^{\circ}C.$

$\begin{array}[t]{rll} f‘(2) &=& (1-0,1\cdot 2)\cdot\mathrm e^{-0,1\cdot 2} \\[5pt] &=& 0,8\cdot \mathrm e^{-0,2} \\[5pt] &\approx& 0,65 \end{array}$

Nach zwei Stunden nimmt die Körpertemperatur der Person mit einer momentanen Änderungsrate von ca. $0,65^{\circ}\,C$ pro Stunde zu.

Die Zu- und Abnahme der Körpertemperatur wird durch die erste Ableitungsfunktion $\(f$ beschrieben.

Mit dem GTR kann der Tiefpunkt des Graphen von $\(f$ graphisch bestimmt werden:

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 3: minimum

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F3: MIN

Die Koordinaten des Tiefpunkts folgen mit $T(20\mid -0,14).$

Die Körpertemperatur der erkrankten Person nimmt folglich $20$ Stunden nach dem Ausbruch der Krankheit am stärksten ab.

1. Schritt: Zeitraum der Erkrankung bestimmen

Durch Gleichsetzen der Funktion $f(t)$ und der Geraden $y=37,9$ ergibt sich mit dem GTR:

$\blacktriangleright$ TI 84-PLUS

Bestimme die Schnittpunkte des Graphen von $f$ mit der Gerade zu $y = 37,9.$

2nd $\to$ trace (calc) $\to$ 5: intersect

$\blacktriangleright$ Casio fx-CG

Bestimme die $x$ -Werte zum $y$ -Wert $37,9$ mit dem X-CAL-Befehl.

F5 (G-Solv) $\to$ F6 $\to$ F2: X-CAL

Die Schnittstellen folgen mit:

$t_1\approx 1,0$ und $t_2\approx 37,2$

Da sich zwischen den beiden Stellen das Maximum des Graphen befindet, handelt es sich bei dem Intervall $[t_1;t_2]$ um den Zeitraum, in dem die Person Fieber hat.

2. Schritt: Belastungswert bestimmen

Rechnung anzeigen

$\displaystyle\int_{1,0}^{37,2}(f(t)-37,9)=...$

Mit dem GTR folgt:

$\blacktriangleright$ TI 84-PLUS

2nd $\to$ trace (calc) $\to$ 7: $\int f(x)\;\mathrm dx$

$\blacktriangleright$ Casio fx-CG

F5 (G-Solv) $\to$ F6 $\to$ F3: $\int \;\mathrm dx$

$\displaystyle\int_{1,0}^{37,2}(t\cdot \mathrm e^{-0,1t} -0,9)\;\mathrm dt \approx 55,51$

In dem Zeitraum, in dem die erkrankte Person Fieber hat, beträgt der Belastungswert folglich ca. 55,51.

Gesucht ist der Zeitpunkt $b,$ für den gilt:

$\displaystyle\int_{1,0}^{b}(f(t)-37,9)\;\mathrm = \; 25$

Durch Ausprobieren mit dem GTR ergeben sich folgende Werte:

$\begin{array}[t]{rll} \displaystyle\int_{1,0}^{13}(t\cdot \mathrm e^{-0,1t} -0,9)\;\mathrm dt &\approx& 26,05 \\[5pt] \displaystyle\int_{1,0}^{12}(t\cdot \mathrm e^{-0,1t} -0,9)\;\mathrm dt &\approx& 23,37 \\[5pt] \displaystyle\int_{1,0}^{12,5}(t\cdot \mathrm e^{-0,1t} -0,9)\;\mathrm dt &\approx& 24,72 \\[5pt] \displaystyle\int_{1,0}^{12,7}(t\cdot \mathrm e^{-0,1t} -0,9)\;\mathrm dt &\approx& 25,25 \\[5pt] \displaystyle\int_{1,0}^{12,6}(t\cdot \mathrm e^{-0,1t} -0,9)\;\mathrm dt &\approx& 24,99\\[5pt] \end{array}$

Ca. 12,7 Stunden nach Ausbruch der Krankheit überschreitet die Belastung der erkrankten Person somit den Wert von 25.

1. Schritt: Abnahmegeschwindigkeit berechnen

$\begin{array}[t]{rll} f‘(20) &=& (1-0,1\cdot 20)\cdot \mathrm e^{-0,1\cdot 20} \\[5pt] &=& - \mathrm e^{-2} \\[5pt] &\approx& -0,135 \end{array}$

Da die lineare Abnahme doppelt so schnell wie die Abnahme im beschriebenen Modell erfolgt, ist diese gegeben durch $m = -0,135\cdot 2 = -0,27.$

2. Schritt: Lineare Funktionsgleichung aufstellen

Die lineare Abnahme wird durch eine Gerade $g$ mit der Steigung $m\approx -0,27$ beschrieben. Diese muss an der Stelle $t=20$ den Graphen von $f$ schneiden. Es muss also gelten:

$\begin{array}[t]{rll} g(20) &=& f(20) \\[5pt] &=& 37 + 20\cdot \mathrm e^{-0,1\cdot 20} \\[5pt] &\approx& 39,71 \end{array}$

Durch Einsetzen der Steigung $m$ sowie der Koordinaten des Schnittpunktes $S(20\mid 39,71 )$ in die allgemeine Geradengleichung folgt:

Rechenweg anzeigen

$b \approx 45,11$

Die lineare Abnahme nach der Einnahme des fiebersenkenden Medikaments kann somit durch folgende Funktionsgleichung beschrieben werden:

$g(t)= - 0,27 \cdot t + 45,11$

3. Schritt: Fieberfreien Zeitpunkt bestimmen

$\begin{array}[t]{rll} g(t) &=& 37,9 \\[5pt] - 0,27 \cdot t + 45,11 &=& 37,9 & \\[5pt] \end{array}$

Mit dem solve-Befehl des GTR folgt $t\approx 26,7.$

Mit Medikamenteneinnahme ist die erkrankte Person also bereits 26,7 Stunden nach Ausbruch der Krankheit fieberfrei. Ohne das Medikament ist sie erst ca. 37,2 Stunden nach Ausbruch fieberfrei. Durch das Medikament ist die erkrankte Person also 10,5 Stunden früher fieberfrei.

Der $y$ -Achsenabschnitt der Tangente wird durch den Term $37+0,1p^2\cdot \mathrm e^{-0,1p}$ beschrieben. Gesucht werden folglich die Extremstellen des Terms.

1. Schritt: Ableitungsfunktionen bilden

$\begin{array}[t]{rll} y(p) &=& 37+0,1p^2\cdot \mathrm e^{-0,1p} \\[10pt] \end{array}$

Mit der Produkt- und Kettenregel folgt:

Ableitungen anzeigen

2. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\begin{array}[t]{rll} y‘(p) &=& 0 \\[5pt] (0,2p -0,01p^2)\cdot \mathrm e^{-0,1p} &=& 0 &\quad \scriptsize \mid\;: \mathrm e^{-0,1p} \\[5pt] 0,2p -0,01p^2 &=& 0 \\[5pt] p\cdot(0,2-0,01p)&=& 0 & \\[5pt] \end{array}$

Mit dem Satz vom Nullprodukt folgt die erste Nullstelle mit $p_1=0.$ Die zweite Nullstelle ergibt sich wie folgt:

$\begin{array}[t]{rll} 0,2-0,01p_2 &=& 0 &\quad \scriptsize \mid\;-0,2 \\[5pt] -0,01p_2 &=& -0,2 &\quad \scriptsize \mid\; :(-0,01)\\[5pt] p_2 &=& 20 \end{array}$

3. Schritt: Hinreichende Bedingung für Extremstellen anwenden

Rechenweg anzeigen

$\( y$

Rechenweg anzeigen

$\( y$

4. Schritt: $y$ -Koordinaten bestimmen

$\begin{array}[t]{rll} y(0) &=& 37+0,1\cdot 0^2\cdot \mathrm e^{-0,1\cdot 0} \\[5pt] &=& 37 \\[10pt] \end{array}$

$\begin{array}[t]{rll} y(20) &=& 37+0,1\cdot 20^2\cdot \mathrm e^{-0,1\cdot 20} \\[5pt] &=& 37 + 40\cdot \mathrm e^{-2} \\[5pt] &\approx& 42,41 \end{array}$

5. Schritt: Grenzwerte betrachten

Für $p\to \infty$ gilt:

$y(p) = 37+0,1\underbrace{p^2}_{\to\infty}\cdot \underbrace{\mathrm e^{-0,1p}}_{\to 0} \to 37$

Der Graph von $y,$ der den Verlauf der $y$ -Achsenabschnitte beschreibt, nimmt für $p=0$ den kleinsten Funktionswert an. Anschließend steigt er an, bis er bei $p=20$ seinen höchsten Punkt erreicht. Danach fällt der Graph nur noch und nähert sich dabei der Asymptote $y=37$ an. Er erreicht also nur einmal seinen höchsten Wert von 42,41 und seinen kleinsten Wert von 37.

Daher gibt es genau eine Tangente mit dem größtem $y$ -Achsenabschnitt $p =20$ und eine Tangente mit dem kleinstem $y$ -Achsenabschnitt $p=0.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?